Метод Эйлера для системы ду 1-го порядка

Рассмотрим задачу Коши.

Дана система 2-х дифференциальных уравнений:

(5)

при начальных условиях х(t₀)=x₀, y(t₀)=y₀. (6)

Требуется найти функции x=x(t) иy=y(t), являющиеся решением системы (5) и удовлетворяющие условиям (6).

Для отискания ее приближенного численного решения на отрезке [t₀, t₀+a] также применяется метод Эйлера, который реализует такой алгоритм:

1. По заданному n (числу точек деления отрезка) вычисляем шаг h, считая известными x₀, y₀, t₀.

2. Зная x_k, y_k, t_k, подставляя эти значения в правую часть уравнений системы (5), находим ₁(x_k, y_k, t_k), ₂(x_k, y_k, t_k) и вычисляем:

.

И так до тех пор, пока k+1=n, т.е. t_k+1=t_k+a.

Метод Эйлера для решения системы ду 2-го порядка

, (3)

при начальных условиях у(х₀)=у₀, у(х₀)=у₀. (4)

Найти функцию у=(х), являющуюся решением уравнения (3) и удовлетворяющую условиям (4).

Выполним подстановку: y=Z, y=Z.

Уравнение (3) заменим системой:

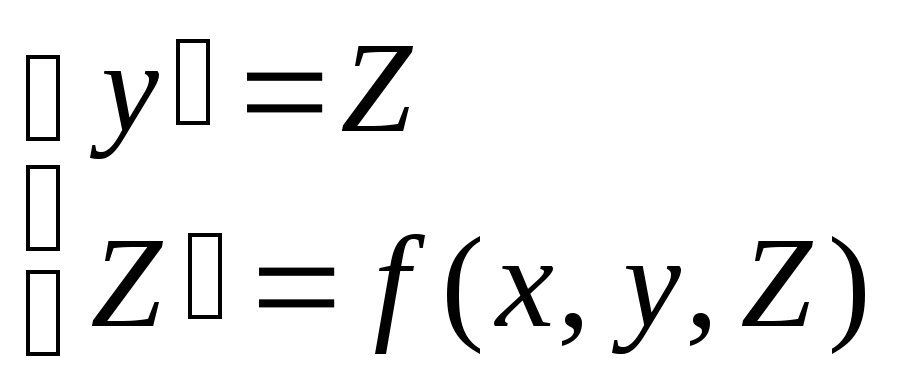
а начальные условия (4) переходят в условия: у(х₀)=у₀, Z(х₀)=Z₀ (Z₀=y₀).

Так что решение задачи (3), (4) сведено к решению задачи (5), (6) при ₁=Z, ₂=(x,y,Z) и может может быть получено по ранее описанному алгоритму.

Пример.

Подпрограмма вычисления:

при заданных условиях.

Таблица решений:

k	0	1	2	3	4	5
tn	0	0,1	0,2	0,3	0,4	0,5
xn	-1	-1	-1,0111	-1,0347	-1,0723	-1,1258
yn	1	0,9	0,8091	0,7265	0,6516	0,5837

Модифицированный метод Эйлера для ду 1-го порядка

При практически том же объеме вычислительной работы дает погрешность порядка h² вместо h в обычном методе Эйлера, что достигается с помощью очень простого приема.

Суть его состоит в том, что на малом отрезке [x, x+h] интегральная кривая у=у(х) уравнения (1) заменяется отрезком прямой линии, проходящим через точку (х, у(х)), но с угловым коэффициентом, несколько иначе определяемым, чем в методе Эйлера.

Пусть отрезок [a;b] разделен на n равных частей с точками х₀, х₁,…, x_n и найдены y₁, y₂,…, y_n – приближенные значения в точках х₀, х₁,…, x_n. Рассматриваем отрезок [x_k, x_k+1] и для определения y_k+1 используем следующие геометрические рассуждения.

Проведем в точке М_k(x_k,y_k) касательную к интегральной кривой, проходящей через точку M_k, т.е. прямую линию, уравнение которой (отрезок M_kM_k+1). Определим координату точки N_k, являющейся точкой пересечения этой прямой и прямой :

Затем найдем значение и из точки М_k(x_k,y_k) проведем прямую с угловым коэффициентом_k: (отрезокM_kM_k+1).

В качестве y_k+1принимаем ординату точкиM_k+1, лежащей на пересечении этой прямой и прямойx=x+h, т.е., где.

Это рекурентная формула модифицированного метода Эйлера.

Алгоритм метода

Пусть заданы уравнение , начальное условие у(х₀)=у₀и отрезок [a;b].

1. Задаем число n дочек деления отрезка [a;b] и определяем шаг интегрирования .

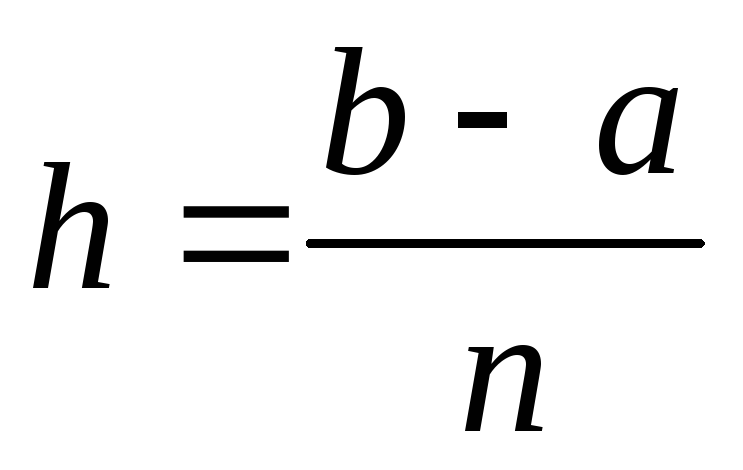2. Пусть определены x_k, y_k. Подставляя их значения в правую часть уравнения (1), находим (x_k, y_k). Вычисляем: .

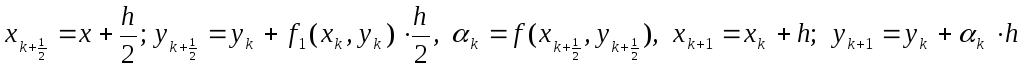Если k+1<n, то повторяем действия 2, считая исходными данными x_k+1, y_k+1. Если k+1=n, то процесс закончен. Числа y₁, y₂,…, y_n приближенно представляют значения искомого уравнения (1) в точках деления х₀, х₁,…, x_n.

Существует несколько модификаций метода Эйлера, суть которых сводится к различным определениям направления _kзвена ломаной из точки (x_k,y_k) в точку (x_k+1,y_k+1). Так, например, знаяx_k,y_k, находят:

.

Эти рекурентные соотношения реализуют так называемый метод Эйлера-Коши.

Отискивая приближенное решение задачи (1), (2) модифицированным методом Эйлера, мы на каждом шаге уточняем угловой коэффициент звеньев ломаной линии и получаем решение точнее, чем по методу Эйлера. Из теории приближенных методов известно, что разность между приближенным значением y_kв точкеx_kи точным значением у(x_k) оценивается неравенством:

.

Поскольку , то эта погрешность имеет порядокна каждом шаге (т.е. переходе отy_kкy_k+1). Однако с каждым шагом происходит накопление погрешности и в точкеx_n=bпогрешность уже будет иметь порядок(что все же будет точнее, чем в методе Эйлера, где погрешность порядка).

Для оценки погрешности приближенного решения у_nв точкеx_n=b, полученного с шагомh, повторяют вычисления с шагом 2h, и абсолютную погрешность(у_n) полагают равной:

,

где - приближенное решение в точке х_n при шаге 2h.

Эта погрешность является оценкой метода и не учитывает погрешность, получаемую за счет округления при вычислениях.

Пример. .

Таблица решения:

k	0	1	2	3	4	5
хk	0	0,2	0,4	0,6	0,8	1
yk	1	1,01	1,040603	1,0936738	1,1725277	1,2822763

Программа решения задачи Коши для системы ДУ 1-го порядка модифицированным методом Эйлера:

Дана система ДУ:

и начальные условия: х(t₀)=x₀, y(t₀)=y₀ и шаг интегрирования h.

Вычисления приближенного решения модифицированным методом Эйлера производится по рекурентным соотношениям, аналогичным формулам (17).

Пусть известны x_k, y_k, t_k. Вычисляем:

Пример.

Таблица решения:

k	0	1	2	3	4	5
tk	0	0,1	0,2	0,3	0,4	0,5
xk	-1	-1,0053	-1,0216	-1,0502	-1,0923	-1,1494
yk	1	0,9048	0,8186	0,7406	0,6701	0,6063