Численное дифференциирование и интегрирование функции одной переменной

1. численное дифференциирование функций с помощью интерполяционных полиномов

Численное дифференциирование применяется при решении задач, в которых нужно найти производную некоторого порядка функции, заданной таблично, или в виде сложного аналитического выражения.

Пусть функция (х) задана значениями у_і=(х_і) в (n+1)-й точке х_і (і=0,1,2,…,n) отрезка [a,b]. Общий метод получения функции численного дифференциирования состоит в аппроксимации табличных значений функции каким-либо интерполяционным многочленом Р_n(x). Искомые значения производных функции в любой точке отрезка [a,b] приближенно выражаются через соответствующее значение производных этого многочлена:

. (1)

Если известна погрешность интер-й формулы , то погрешности производных

. (2)

рассмотрим частные случаи формул численного дифференциирования, в которых функция (х) приближается интерполяцинными полиномами ньютона, лагранжа или сплайнами.

1. применение интерпорляционных формул ньютона.

пусть функция (х), заданная на отрезке [a,b] таблицей значений в равноотстоящих точках х_і (і=0,1,2,…,n) с шагом h=x_i+1-x_i, аппроксимируется интерполяционным полиномом ньютона для интерполяции вперед:

, (3)

где .

последовательно дифференциируя многочлен (3) по переменной х и учитывая, что , получим формулы для приближенного вычисления производных функции (х):

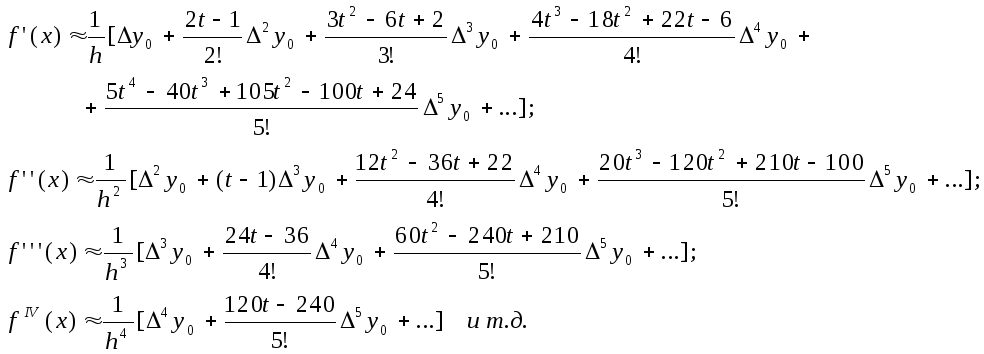(4)

формулы (4) удобно применять, если значение х расположено ближе к левому концу отрезка [a;b]. для вычисления производной в точке, лежащей ближе к правому концу отрезка [a;b], можно воспользоваться интерполяционным полиномом ньютона интерполяции назад:

, (5)

где .

дифференциируя (5), получим формулы для приближенного вычисления производных функции:

(6)

если требуется вычислить производные в узлах интерполяции х_і (і=0,1,2,…,n), то формулы (4) и (6) упрощаются. поскольку левую точку можно принять за начальную, то положив в (4) х=х₀ (t=0), получим формулы для вычисления значений производных:

(7)

аналогично, положив в формуле (6) х=х_n (t=0), получим:

(8)

если в интерполяционном полиноме ньютона (3) ограничиться расстояниями до k-го порядка, то его остаточный член:

(9)

где  - некоторое число, лежащее между узлами интерполяции х₀, х₁,…, х_k и х.

продифференциировав (9) по х и положив х=х₀ (t=0), получим погрешность для первой производной функции:

(10)

на практике оценка (10) мало пригодна, т.к. обычно не известна производная ^(k+1)(x). поэтому при небольших х можно заменить производную ее выражением через конечные разности и представить погрешность в виде:

(11)

аналогично получаются оценки погрешности для производных высших порядков.

следует учесть, что минимальное число узлов, необходимое для вычисления k-й производной, равно k+1. при использовании большого числа узлов получаются формулы более высокого порядка точности.

пример. пусть функция задана таблицей значений с шагом h=0,1:

xi	0	0,1	0,2	0,3	0,4	0,5
yi	1	0,99	0,9608	0,9139	0,8524	0,7788

вычислим приближенно значения производных ’(0) и ’’(0). составим таблицу конечных разностей:

x	y	y	2y	3y	4y	5y
0 0,1 0,2 0,3 0,4 0,5	1 0,99 0,9608 0,9139 0,8524 0,7788	-0,01 -0,0292 -0,0469 -0,0615 -0,0736	-0,0192 -0,0167 -0,0146 -0,0121	0,0025 0,0021 0,0025	-0,0004 0,0004	0,0008

воспользуемся формулой (7), полагая х=х₀ и ограничиваясь разностями четвертого порядка:

точные значения производных равны соответственно:

выразим погрешность через конечные разности пятого порядка по (7):

следует отметить, что с увеличением порядка производной точность формул численного дифференциирования резко падает. на практике их применяют для вычисления производных не выше 2-го порядка.

2. применение интерполяционного полинома лагранжа.

функцию (х), заданную на отрезке [a;b] значениями y_i=(x_i) в равноотстоящих точках х_i (i=0, 1, 2,…, n), h=(x_i+1-x_i), заменим приближенно интерполяционным многочленом лагранжа:

, где . (12)

продифференциируем (12) по х:

(13)

учитывая выражение для погрешности интерполяционной формулы лагранжа

, (14)

после дифференциирования получим оценку погрешности для производной функции в узлах интерполяции:

, где . (15)

в формуле (13) производная функция выражается не через конечные разности, а через ее значения в узлах интерполяции. випишем некоторые ее частные случаи, позволяющие вычислять производные функции и их погрешности в узлах при фиксированном h.

1. при n=2 (заданы значения функции в 3-х точках) получим значения первых производных:

(16)

и вторых производных:

(17)

б) при n=3 (четыре узла интерполяции) получим выражения для первых производных:

(18)

и вторых производных:

(19)

на практике наиболее применимы следующие формулы численного дифференциирования для любого внутреннего узла х_i:

(20)

(21)

(22)

которые могут быть получены из (14), (16), (17) и (19).

отметим, что с уменьшением шага h для достаточно гладкой формулы величина остаточного члена в формулах дифференциирования, т.е. погрешность метода уменьшается. при этом значения производных более точны в узлах, расположенных посредине равномерной сетки. вычислительная погрешность, вызванная неточным заданием значений функции y_i, а также ошибками, возникающими при вычислении конечных разностей, увеличивается при уменьшении n и росте порядка производной. как видно из (20)-(22), при малых h значения функции в соседних узлах почти равны, поэтому при вычислении их разности теряются значащие цифры. деление на h^k, если h мало, может привести к большой абсолютной погрешности в значениях k-й производной. таким образом задача аппроксимации производных является по своей природе неустойчивой.

если функция задана в узлах с абсолютной погрешностью , то для конкретной формулы численного дифференциирования можно применить указать оптимальный шаг. например, определим ошибку метода для (21) , где , и ошибку, вызванную погрешностью исходных данных, .

суммарная погрешность (без учета ошибок округления): (23) принимает минимальное значение при .

проведя аналогичные рассуждения для (22), получим следующее выражение для оптимального шага:

, где . (24)

формулы (23) и (24) можно применять в том случае, если известны оценки соответствующих производных.

оценку погрешности формулы численного дифференциирования можно проводить по правилу рунге, если остаточный член формулы имеет структуру:

, k=1, 2, … (25)

вычислим производную по указанной формуле на равномерной сетке узлов сначала с шагом h, а затем с шагом rh.

учитывая, что , , получим следующую оценку погрешности:

. (26)

тогда исходную формулу численного дифференциирования р-го порядка можно уточнить, полагая:

, k=1, 2, … (27)

3. численное дифференциирование функций с помощью сплайнов

как уже отмечалось, интерполяционные сплайны обеспечивают хорошее приближение не только функции (х), заданной на сетке , но и ее производных. для вычисления производных достаточно продифференциировать интерполяционный сплайн соответствующее число раз.

для интерполяционных кубических сплайнов формулы численного дифференциирования, выраженные через наклоны и моменты , имеют вид:

; (28)

; (29)

; (30)

; (31)

(32)

(33)

где .

если , то порядок приближения производных ’(x), ’’(x) и ’’’(x) сплайнами s’(x), s’’(x) и s’’’(x) равен соответственно о(h³), o(h²) и o(h).

если в качестве базиса взяты кубические в-сплайны, то производные аппроксимирующей функции выражаются через производные в-сплайнов:

, r=1, 2, 3. (34)

алгоритмы вычисления m_i, m_i и c_i изложены в главе 5. если воспользоваться локальной аппроксимальной матрицей функции и положить с_i=y_i (i=0, 1, 2,…, n), то производные сплайна:

, r=1, 2, 3. (35)

значения производных функции (х) в узлах интерполяции х_і (і=0, 1, 2,…, n) приближенно приравниваем к значениям соответствующих производных кубического сплайна. получим следующие формулы численного дифференциирования в узлах:

i=0, 1,…, n; (36)

i=0, 1,…, n-1; (37)

i=0, 1,…, n; (38)

i=0, 1,…, n; (39)

i=0, 1,…, n-1; (40)

i=0, 1,…, n; (41)

i=0, 1,…, n-1; (42)

i=0, 1,…, n-1; (43)

, r=1, 2, 3; i=0, 1,…, n. (44)

если выбрать сетку  равномерной с шагом h, а число узлов интерполяции достаточно большим, то внутри промежутка [a;b] точность аппроксимации производной функции повышается. для равномерной сетки значения производных нормализованных кубических в-сплайнов приведены в табл. 5.5. учитывая (6.44), получим:

i=0, 1,…, n; (45)

i=0, 1,…, n; (46)

комбинируя сплайновую и разностную аппроксимацию, можно получить формулы численного дифференциирования более высокого порядка точности [18 «завьялов ю.с. методы сплайн-функций»]:

(47)

(48)

(49)

(50)

i=0, 1,…, n-1; (51)

если значения функции (х) заданы с абсолютной погрешностью  на густой сетке, то для численного дифференциирования строится интерполяционный сплайн на более редкой сетке узлов. оптимальный по порядку шаг сетки выбирается , что согласуется с формулой (24) для полиномиальной интерполяции [28 «стечкин. сплайны в выч.мат.»!!!].

вычисление второй производной функции (х) можно осуществить дифференциированием сплайна от сплайна [1 «альберг. теория сплайнов и ее применение»]. при этом вначале вычисляются наклоны по заданным значениям функции, а затем вычисляется сплайн, интерполирующий в узлах значения m_i. производная построенного сплайна приближает вторую производную функции.