Повний факторний експеримент (пфе)

ПФЕ - це екс­пе­ри­мент, при яко­му ре­а­лі­зу­ю­ть­ся усі мо­ж­ли­ві ко­м­бі­на­ції рі­в­нів і фа­к­то­рів. Як­що фа­к­то­ри ва­рі­ю­ю­ть­ся на двох рі­в­нях, тобто (+1) і (-1), то чи­с­ло до­сві­дів при ПФЕ до­рі­в­нює

N=2ⁿ

План про­ве­ден­ня екс­пе­ри­мен­ту зви­чай­но пре­д­ста­в­ля­є­ть­ся у ви­гля­ді ма­т­ри­ці, ко­ж­ний ря­док якої яв­ляє со­бою зна­чен­ня фа­к­то­рів (зви­чай­но в ко­до­ва­ній шка­лі). За­пи­ше­мо план про­ве­ден­ня екс­пе­ри­мен­ту при n=2

u	x1	x2
1	+1	+1
2	-1	+1
3	+1	-1
4	-1	-1

n=3

u	x1	x2	x3	yu1	yu2	yu3
1	+1	+1	+1	y11	y12	y13
2	-1	+1	+1	y21	y22	y23
3	+1	-1	+1	y31	y32	y33
4	-1	-1	+1	y41	y42	y43
5	+1	+1	-1	y51	y52	y53
6	-1	+1	-1	y61	y62	y63
7	+1	-1	-1	y71	y72	y73
8	-1	-1	-1	y81	y82	y83

Зви­чай­но рі­в­ні фа­к­то­рів пла­ну по­зна­ча­ють че­рез ‘+’, ‘-' для зме­н­шен­ня по­хиб­ки екс­пе­ри­мен­ту, як-­от впли­ву на ви­хі­д­ну ве­ли­чи­ну ви­пад­ко­вих, що не вра­хо­ву­ю­ть­ся фа­к­то­рів, що іс­то­т­но мо­жуть спо­т­во­ри­ти ре­зуль­та­ти на­сту­п­них до­слі­дів в екс­пе­ри­мен­ті. Крім то­го, для під­ви­щен­ня то­ч­но­с­ті мо­де­лі екс­пе­ри­мен­ти по­вто­рю­ю­ть­ся де­кіль­ка ра­зів на ко­ж­но­му рі­в­ні. При об­ро­б­ці ре­зуль­та­тів ви­ко­ри­с­то­ву­є­ть­ся се­ре­д­нє зна­чен­ня ви­хі­д­ної ве­ли­чи­ни.

- середнє значення величини.

Роз­г­ля­не­мо ме­то­ди­ку ви­зна­чен­ня ко­е­фі­ці­є­н­тів мо­де­лі на при­кла­ді n=2. У цьо­му ви­пад­ку ви­зна­ча­є­ть­ся мо­дель ви­ду

у=₀+₁х₁+₂х₂

То­му що ви­хі­д­на ве­ли­чи­на у ви­зна­ча­є­ть­ся по ста­ти­с­ти­ч­ним да­ним, то при ви­зна­чен­ні ко­е­фі­ці­є­н­тів мо­де­лі ₀, ₁, ₂ ми одер­жу­є­мо не­то­ч­ні зна­чен­ня, а їх­ні ста­ти­с­ти­ч­ні оцін­ки, що по­зна­ча­ю­ть­ся b₀, b₁, b₂. Шу­ка­на мо­дель на­бу­ває вид

=b₀+b₁х₁+b₂х₂

Для ви­зна­чен­ня цих ста­ти­с­ти­ч­них оці­нок b₀, b₁, b₂ зви­чай­но ви­ко­ри­с­то­ву­є­ть­ся ме­тод най­ме­н­ших ква­д­ра­тів, а са­ма про­це­ду­ра від­шу­ку­ван­ня ко­е­фі­ці­є­н­тів мо­де­лі з їх­нім по­даль­шим ана­лі­зом на­зи­ва­є­ть­ся ре­г­ре­си­в­ним ана­лі­зом. У за­да­чах ре­г­ре­си­в­но­го ана­лі­зу за­сто­со­ву­є­ть­ся на­сту­п­не до­пу­щен­ня:

1. усі змін­ні х₁, х₂, …, х_n є не­за­ле­ж­ни­ми не­ви­пад­ко­ви­ми змін­ни­ми, що за­да­ю­ть­ся аб­со­лю­т­но то­ч­но;

2. ви­пад­ко­ва ве­ли­чи­на у_i під­по­ряд­ко­ву­є­ть­ся нор­маль­но­му за­ко­ну роз­по­ді­лу, а усі ди­с­пер­сії в окре­мих то­ч­ках фа­к­то­р­но­го про­с­то­ру од­но­рі­д­ні.

Відповідно до методу найменших квадратів визначаються нев’язки

_u=y_u-_u= y_u-( b₀+b₁х₁+b₂х₂)

Для спро­щен­ня роз­ра­хун­ків у план про­ве­ден­ня екс­пе­ри­мен­ту вво­ди­ть­ся ну­льо­вий фі­к­ти­в­ний (умо­в­ний) фа­к­тор скрізь рі­в­ний 1.

u	x1	x2
1	+1	+1
2	-1	+1
3	+1	-1
4	-1	-1

Чи­с­ло нев’язок до­рі­в­нює чи­с­лу до­слі­дів. Від­по­ві­д­но до ме­то­ду най­ме­н­ших ква­д­ра­тів ми по­вин­ні ви­зна­чи­ти ко­е­фі­ці­є­н­ти b₀, b₁, b₂, які до­ста­в­ля­ють мі­ні­маль­ні зна­чен­ня ви­ра­зу

Для визначення невідомих коефіцієнтів необхідно розв'язати систему:

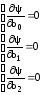
Тоді одержимо систему рівнянь:

Гі­д­ні­с­тю пла­нів ПФЕ є про­с­то­та ви­зна­чен­ня ко­е­фі­ці­є­н­тів мо­де­лі, що яв­ля­є­ть­ся рі­в­нян­ням ре­г­ре­сії. Ма­т­ри­ця пла­ну­ван­ня екс­пе­ри­мен­ту во­ло­діє вла­с­ти­во­с­тя­ми:

1. ортогональності;

2. нормування;

3. симетрії;

4. рототабельності.

Ор­то­го­наль­ність - вла­с­ти­вість, при якій су­ма до­бу­т­ків по ряд­ках двох будь-­яких стов­п­чи­ків ма­т­ри­ці до­рі­в­нює ну­лю.

де i, j – будь-які стовпчики матриці;

N – кількість експериментів.

Нор­му­ван­ня - вла­с­ти­вість, при якій су­ма ква­д­ра­тів будь-­яко­го стов­п­чи­ка ма­т­ри­ці до­рі­в­нює чи­с­лу рі­з­но­ма­ні­т­них до­слі­дів.

де i – будь-який стовпчик матриці.

Си­ме­т­рія - вла­с­ти­вість, при якій ал­ге­б­ра­ї­ч­на су­ма еле­мен­тів будь-­яко­го ре­аль­но­го фа­к­то­ра до­рі­в­нює ну­лю по стов­п­чи­ку.

де i – будь-який стовпчик матриці.

Ро­то­та­бе­ль­ність - ін­ва­рі­ан­тість до обер­тан­ня си­с­те­ми, по­ля­гає в то­му, що ди­с­пер­сії пе­ре­дба­че­них зна­чень від­гу­ку на рі­в­них від­ста­нях від цен­т­ру пла­ну постій­ні і мі­ні­маль­ні.

Використовуючи властивості ПФЕ, одержимо:

, где i=0,1,2.

Роз­г­ля­не­мо по­ка­за­ну ме­то­ди­ку ви­зна­чен­ня ко­е­фі­ці­є­н­тів рі­в­нян­ня ре­г­ре­сії на n фа­к­то­рів.

, где i= 0, 1, 2, …, n.