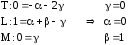matmodeom / MMM_Lek / U_M_d_6

Плани другого порядку

У тих ви­пад­ках, ко­ли до­слі­джу­ва­ний об'єкт не мо­же бу­ти аде­к­ва­т­но опи­са­ний лі­ній­ною мо­дел­лю, вар­то ви­ко­ри­с­то­ву­ва­ти фун­к­ції від­гу­ку у ви­гля­ді кри­вих дру­го­го по­ряд­ку.

За­сто­со­ву­ва­ти при­йо­ми, що ви­ко­ри­с­то­ву­ва­ли­ся при ура­ху­ван­ні не­лі­ній­но­с­ті до­бу­т­ку фа­к­то­рів, тут не мо­ж­на. То­му що за­вж­ди буде рівно ­од­иниці­, т­обто ­в дан­ом­у ­випадк­у­ б­уде пору­ше­на­ вла­ст­и­вість о­рт­о­гональн­ості і сим­ет­рі­ї план­у. Для­ п­обудо­ви ­плану­ ­друго­го­ п­о­ря­дк­у ­можна­ ­ви­ко­ри­с­товува­ти різноман­іт­ні плани­, ­що от­рим­ані­ на ос­н­ов­і ­д­отрима­нн­я ­влас­ти­в­остей о­рт­о­гонально­сті ­і сим­е­трії.­ На­йб­іл­ь­ше­ част­о ­за­стос­овують­с­я ор­тог­она­ль­ні­ це­нтраль­но-композицій­ні­ план­и (­ОЦКП) др­уг­ого п­ор­яд­ку. У­ основу­ побуд­ови­ т­аких планів­ покла­де­ний­ ПФЕ ­шляхом­ додава­нн­я нових точ­о­к ­(зоря­н­их­) для кожно­г­о фактора х_i н­а рівн­ях ­.­ ­При ц­ьому значення і­н­ших ко­ор­ди­на­т рівні нулю,­ т­об­то ці точки знах­одяться на о­сях коор­ди­нат (х­_i­=­). В­ідстань від ­нуля до зорян­ої­ ­то­ч­ки­ нази­в­аєтьс­я ­з­оряни­м ­пл­ечем. Крім того, у план добав­ля­єт­ься т­о­чка по­чатку ­ко­ордин­ат ­(х_i = 0, i = 1, 2, …, n). Покажемо точки плану другого порядку при n=2.

x₂

(0,)

(1,1)

(-1,1)

(,0)

(-,0)

(0,0)

x₁

(1,-1)

(-1,-1)

(0,-)

Та­ким чи­ном, чи­с­ло до­слі­дів пла­ну дру­го­го по­ряд­ку об­чи­с­лю­є­ть­ся по фор­му­лі:

N=2ⁿ+2n+1

n=3 N=2³+23+1=15

x₂

x₁

x₃

По­ло­жен­ня зо­ря­них то­чок за­ле­жить від чи­с­ла що ва­рі­ю­ю­ть­ся фа­к­то­рів. На­яв­ність зо­ря­них то­чок за­без­пе­чує ор­то­го­наль­ність пла­ну. При по­бу­до­ві ОЦКП не­об­хід­но пе­ре­тво­ри­ти ква­д­ра­ти фа­к­то­рів, ви­ко­ри­с­то­ву­ю­чи фор­му­ли:

i= 1, 2, …, n

де d – коефіцієнт, що залежить від числа факторів.

Приведемо таблицю значень і d для різноманітних видів ОЦКП.

Число факторів	Ядро плану	Зоряне плече	Величина d	Число точок
1	ПФЕ 22	1,0	0,667	9
2	ПФЕ 23	1,215	0,730	15
3	ПФЕ 24	1,414	0,870	25
4	ДФЕ 25-1	1,547	0,770	27
5	ПФЕ 25	1,596	0,863	43
6	ДФЕ 26-1	1,724	0,843	45

Роз­та­шо­ву­ю­чи ци­ми да­ни­ми, мо­ж­на по­бу­ду­ва­ти будь-­які ОЦКП 2-го по­ряд­ку. По­ка­же­мо це на при­кла­ді при n=2.

u	x0	x1	x2			x1x2
1	+1	1	1			+1
2	+1	+1	1			1
3	+1	1	+1			1
4	+1	+1	+1			+1
5	+1	1,0	0			0
6	+1	+1,0	0			0
7	+1	0	1,0			0
8	+1	0	+1,0			0
9	+1	0	0			0

Даний план має властивості ортогональності і симетрії.

Для обчислення коефіцієнтів моделі 2-го порядку використовуються формули:

де N – кількість дослідів;

n – кількість факторів;

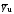середнє значення вихідної величини в u-ому рядку.

У цій формулі не можна в знаменнику записувати N.

i, j= 1, 2, …, n ij

Отримані коефіцієнти використовуються у формулі:

Представимо замість . Одержимо:

Об­роб­ку ре­зуль­та­ту екс­пе­ри­мен­ту і йо­го оці­ню­ван­ня мо­ж­на ви­ко­ну­ва­ти з ви­ко­ри­с­тан­ням ра­ні­ше опи­са­них ета­пів.

Основи теорії подоби й аналізу розмірності

Зме­н­ши­ти кіль­кість до­слі­дів і в ос­та­то­ч­но­му під­су­м­ку їх­ню вар­тість мо­ж­на за ра­ху­нок за­сто­су­ван­ня без­ро­з­мі­р­них ко­м­бі­на­цій ве­ли­чин, отри­ма­них на ос­но­ві те­о­рії по­до­би й ана­лі­зу роз­мі­р­но­с­ті. Те­о­рія по­до­би грун­ту­є­ть­ся на трьох те­о­ре­мах, що вста­но­в­лю­ють зв'я­зок між ве­ли­чи­на­ми, що ха­ра­к­те­ри­зу­ють при­ро­ду до­слі­джу­ва­но­го про­це­су. Від­по­ві­д­но до те­о­ре­ми 1 не­об­хід­ною умо­вою по­до­би двох си­с­тем є рі­в­ність від­по­ві­д­них кри­те­рі­їв по­до­би, що скла­да­ю­ть­ся з па­ра­ме­т­рів цих си­с­тем.

Те­о­ре­ма 2 ( -те­о­ре­ма).

Вся­ке по­в­не рі­в­нян­ня фі­зи­ч­но­го про­це­су, за­пи­са­не у пе­в­ній си­с­те­мі оди­ниць, мо­же бу­ти по­да­но за­ле­ж­ні­с­тю між кри­те­рі­я­ми по­до­би, тобто рі­в­нян­ням, що зв'я­зує без­ро­з­мі­р­ні ве­ли­чи­ни.

Те­о­ре­ма 3 (обе­р­не­на).

Фор­му­лює умо­ви не­об­хід­ні і до­ста­т­ні для пра­к­ти­ч­ної ре­а­лі­за­ції по­до­би. Во­на ствер­джує: для по­до­би явищ по­вин­ні бу­ти від­по­ві­д­но од­на­ко­ви­ми ви­зна­чаль­ні кри­те­рії по­до­би і по­ді­б­ні умо­ви од­но­зна­ч­но­с­ті.

Для пра­ви­ль­но­го за­сто­су­ван­ня ме­то­дів ана­лі­зу роз­мі­р­но­с­ті тре­ба ма­ти у своє­му роз­по­ря­джен­ні по­в­ний спи­сок змін­них, що впли­ва­ють на екс­пе­ри­мент (чи­с­ло фа­к­то­рів). Зме­н­ши­ти чи­с­ло фа­к­то­рів мо­ж­на за ра­ху­нок за­сто­су­ван­ня пер­шої ча­с­ти­ни те­о­ре­ми Бу­кин­ге­ма: як­що де­яке рі­в­нян­ня од­но­рі­д­но що­до роз­мі­р­но­с­ті, то йо­го мо­ж­на пе­ре­тво­ри­ти до спів­від­но­шен­ня, що мі­с­тить без­ро­з­мі­р­ні ко­м­бі­на­ції ве­ли­чин.

Од­но­рі­д­ни­ми що­до роз­мі­р­но­с­ті на­зи­ва­ють рі­в­нян­ня, фор­ма яких не за­ле­жить від ви­бо­ру ос­но­в­них оди­ниць ви­мі­рів. Без­ро­з­мі­р­ні ко­м­бі­на­ції - спів­від­но­шен­ня (дро­би), скла­де­ні та­ким чи­ном, що усі роз­мі­р­но­с­ті ско­ро­чу­ю­ть­ся. У ре­зуль­та­ті пе­ре­хо­ди­мо до без­ро­з­мі­р­них ко­м­бі­на­цій ве­ли­чин, тобто -кри­те­рі­ям, екс­пе­ри­мент зна­ч­но спро­щу­є­ть­ся за ра­ху­нок зме­н­шен­ня чи­с­ла змін­них, що ва­рі­ю­ю­ть­ся. Одер­жан­ня -кри­те­рі­їв від­бу­ва­є­ть­ся на ос­но­ві ме­то­дів Ре­лея, від­по­ві­д­но до яко­го при­зво­дять ви­хі­д­ну си­с­те­му змін­них до де­якої си­с­те­ми ос­но­в­них оди­ниць (на­при­к­лад, си­с­те­ми ча­су Т, ма­си М, дов­жи­ни L), під­ста­в­ля­ю­чи спів­від­но­шен­ня фор­мул роз­мі­р­но­с­тей в ос­но­в­не рі­в­нян­ня і, роз­в'я­зав йо­го що­до не­ві­до­мих по­ка­з­ни­ків сту­пе­нів, одер­жи­мо без­ро­з­мі­р­ні ко­м­бі­на­ції.

Ма­те­ма­ти­ч­на пе­ре­вір­ка ре­зуль­та­тів ана­лі­зу роз­мі­р­но­с­тей здій­с­ню­є­ть­ся на ос­но­ві дру­гої ча­с­ти­ни те­о­ре­ми Бу­кин­ге­ма. Як­що іс­нує од­но­зна­ч­не спів­від­но­шен­ня між m фі­зи­ч­ни­ми ве­ли­чи­на­ми, у на­пи­сан­ні яких ви­ко­ри­с­то­ву­є­ть­ся n не­за­ле­ж­них па­ра­ме­т­рів, то іс­ну­ють спів­від­но­шен­ня ви­ду

(А₁, А₂, …, А_m)=0 (₁, ₂, …, _m-n)=0

між (m-n) без­ро­з­мі­р­ною ко­м­бі­на­ці­єю. Для ви­зна­чен­ня кри­те­рію по­до­би тре­ба ви­ко­на­ти по­слі­до­в­ність дій:

1. Ви­ді­ли­ти m па­ра­ме­т­рів А₁, А₂, …, А_m, які ха­ра­к­те­ри­зу­ють до­слі­джу­ва­ний про­цес;

2. Скла­с­ти ма­т­ри­цю роз­мі­р­но­с­тей цих m па­ра­ме­т­рів, об­ра­в­ши ос­но­в­ні фі­зи­ч­ні ве­ли­чи­ни ви­мі­ру;

3. Встановити n незалежних між собою параметрів;

4. Представити опис досліджуваного процесу в формі критерію.

1. По­ка­же­мо ви­зна­чен­ня -кри­те­рі­їв для ви­пад­ку ви­зна­чен­ня за­ле­ж­но­с­ті стій­ко­с­ті ін­ст­ру­мен­ту від швид­ко­сті, по­да­ча, гли­би­ни рі­зан­ня, си­ли рі­зан­ня, на­пру­ги в зо­ні рі­зан­ня.

Т_ст=f(v,S,t,P,N)

2. Скла­де­мо ма­т­ри­цю роз­мі­р­но­с­ті цих ве­ли­чин, ви­ко­ри­с­то­ву­ю­чи фі­зи­ч­ні ве­ли­чи­ни Т (час), М (ма­са), L (дов­жи­на).

Т_ст [T]¹[L]⁰[M]⁰ с

v [T]^-1[L]¹[M]⁰ м/с

S [T]⁰[L]¹[M]⁰ мм/об

P [T]^-2[L]¹[M]¹ Н=кг м/с²

N [T]^-2[L]^-1[M]¹ Н/м²=кг/м с²

t [T]⁰[L]¹[M]⁰ м

3. Для перевірки складемо матрицю розмірностей із цих величин

det D=-10 – вибір зроблений правильний

4. Таким чином, треба визначити -критерій.

₁=f(₂, ₂)

Для одержання -критеріїв треба:

а) записати загальний вид критеріїв

б) ви­зна­чи­ти по­ка­з­ни­ки сту­пе­нів , , . Мо­ж­на ско­ри­с­та­ти­ся дво­ма спо­со­ба­ми:

1. за допомогою визначників

₁=1 ₁=0 cм/см^-1=1

2. за­сто­со­ву­є­ть­ся, ко­ли кіль­кість змін­них ма­ло й об­чи­с­лен­ня по­ка­з­ни­ків сту­пе­нів мо­ж­на ви­ко­на­ти без об­чи­с­лен­ня ви­зна­ч­ни­ків. Ви­ра­жа­ю­чи ве­ли­чи­ни, що вхо­дять у кри­те­рії по­до­би, че­рез ос­но­в­ні оди­ни­ці ви­мі­ру і при­рі­в­ню­ю­чи по­ка­з­ни­ки сту­пе­нів чи­се­ль­ни­ка і зна­мен­ни­ка при від­по­ві­д­них фі­зи­ч­них ве­ли­чи­нах, мо­ж­на лег­ко ви­зна­чи­ти , , .

При

При

При