matmodeom / MMM_Lek / U_M_d_5

Обробка й оцінка

експериментальних даних

У ре­зуль­та­ті про­ве­ден­ня ба­га­то­фа­к­то­рного екс­пе­ри­мен­ту одер­жу­є­мо зна­чен­ня ви­хі­д­ної ве­ли­чи­ни y_uj, де u= 1, 2, …, N, N – кіль­кість до­слі­дів, j= 1, 2, …, n, n – кіль­кість по­вто­рення до­слі­дів при то­му самому спо­лу­чен­ні фа­к­то­рів, y_uj – зна­чен­ня фун­к­ції від­гу­ку.

Для під­ви­щен­ня то­ч­но­с­ті екс­пе­ри­мен­таль­них да­них найчастіше в ко­ж­ній то­ч­ці фа­к­то­р­но­го екс­пе­ри­мен­ту ста­в­ля­ть­ся рі­в­но­бі­ж­ні до­слі­ди. Че­рез по­хиб­ки ви­мі­рів і дії не­кон­т­ро­льо­ва­них збу­рю­ю­чих фа­к­то­рів всі отри­ма­ні зна­чен­ня y_uj бу­дуть яв­ля­ти со­бою не­за­ле­ж­ні ви­пад­ко­ві ве­ли­чи­ни. З урахуванням цьо­го роз­г­ля­не­мо ме­то­ди­ку об­роб­ки екс­пе­ри­мен­таль­них да­них на ос­но­ві методів ма­те­ма­ти­ч­ної ста­ти­с­ти­ки і ре­г­ре­си­в­но­го ана­лі­зу. Об­роб­ка екс­пе­ри­мен­таль­них да­них у те­о­рії пла­ну­ван­ня екс­пе­ри­мен­ту до­ста­т­ньо до­б­ре фор­ма­лі­зо­ва­ні, лег­ко ре­а­лі­зу­є­ть­ся на ЕОМ і ді­ли­ть­ся на ряд ета­пів. Перехід від од­но­го ета­пу до ін­шо­го здій­с­ню­є­ть­ся пі­с­ля ана­лі­зу по­пе­ре­дньо­го ета­пу.

u	фактори				yuj, j
	x1	x2	…	xm		1	2	…	n
1	x11	x12	…	x1n		y11	y12	…	y1n
2	x21	x22	…	x2n		y21	y22	…	y2n
3	x31	x32	…	x3n		y31	y32	…	y3n
…	…	…	…	…		…	…	…	…	…
N	xN1	xN2	…	xNn		yN1	yN2	…	yNn

y_uj – обмірювана вихідна величина.

Етап 1. Визначення однорідності виміру.

Ви­ко­ну­є­ть­ся з ме­тою ви­клю­чен­ня яв­но гру­бих аномальних похибок, що мо­жуть зна­ч­но спотворити ре­зуль­та­ти екс­пе­ри­мен­ту. Для цьо­го в окре­мих ряд­ках про­ва­ди­ть­ся перевірка од­но­рі­д­но­с­ті зна­чень y_uj за до­по­мо­гою кри­те­рію Стью­ден­та. Розрахункові зна­чен­ня кри­те­рію об­чи­с­лю­ю­ть­ся по фор­му­лі

де най­ме­н­ше або най­біль­ше зна­чен­ня ви­хі­д­ної ве­ли­чи­ни в u-ому ряд­ку, що ми вва­жа­є­мо помилковим;

середнє зна­чен­ня ви­хі­д­ної ве­ли­чи­ни в u-ому ряд­ку, що ми вва­жа­є­мо помилковим без ура­ху­ван­ня .

S_u – оцінка середнього відхилення від середнього значення.

n_u – кількість повторень дослідів у u-ому рядку.

Розрахункові зна­чен­ня критерію Стью­ден­та до­рі­в­ню­ю­ть­ся з таб­ли­ч­ним зна­чен­ням, тобто з чи­с­лом ступенів сво­бо­ди f=n_u-1 і ви­б­ра­ним рі­в­нем зна­чи­мо­с­ті , що ча­с­ті­ше в тех­ні­ці при­ймає зна­чен­ня 0,05, що озна­чає пе­ре­вір­ку гі­по­те­зи з до­вір­чою ймо­ві­р­ні­с­тю

Р=1-

Як­що t_р < t_табл, який ви­би­ра­є­ть­ся зі ста­ти­с­ти­ч­ної таб­ли­ці при f і , то з мо­ж­ли­ві­с­тю Р=1 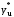є г­рубою ­помил­кою­ і­ його ва­рт­о викл­юч­ити­ з­ ­та­блиці­.­

Реко­мен­дує­ться п­іс­ля ви­ключ­ен­ня гру­бо­г­о рез­ул­ь­та­ту про­вести додатковий дослід, щоб

n_u=n=const

Етап 2. Перевірка статистичної значимості вимірів.

Після перевірки однорідності вимірів обчислюється

З усіх середніх значень визначається і провадиться перевірка значимості по t_р

n_max – кількість повторень дослідів у рядку ;

S_y – оцінка середньоквадратичного відхилення відтворенності досліду (дисперсії).

Розрахункове значення t_р дорівнюється t_табл при числі ступенів свободи f=n_max+n_min і заданою .

Як­що t_р< t_табл, то екс­пе­ри­мент є ма­ло­ін­фор­ма­ти­в­ним, то­му що ма­к­си­маль­не зна­чен­ня від­рі­з­ня­є­ть­ся від мі­ні­маль­но­го не­зна­ч­но і ця рі­з­ни­ця зна­хо­ди­ть­ся в ме­жах пе­ре­шкод (по­ми­л­ки екс­пе­ри­мен­ту). То­му в да­нім ви­пад­ку не­об­хід­но поста­ви­ти та­кий екс­пе­ри­мент, щоб зна­чен­ня ви­хі­д­ної ве­ли­чи­ни в окре­мих то­ч­ках фа­к­то­р­но­го про­с­то­ру від­рі­з­ня­ли­ся іс­то­т­но.

Етап 3. Ви­зна­чен­ня од­но­рі­д­но­с­ті ди­с­пер­сії.

Ви­ко­ну­є­ть­ся за до­по­мо­гою G-критерію Ко­х­ре­на, роз­ра­хун­ко­ве зна­чен­ня яко­го об­чи­с­лю­є­ть­ся по фор­му­лі

де максимальна дисперсія по рядках.

Розрахункові значення дорівнюються з табличними значеннями, що вибираються по ступеню свободи чисельника f₁=n-1, знаменника f₂=N і заданою .

Роз­ра­хун­ко­ві зна­чен­ня до­рі­в­ню­ю­ть­ся з таб­ли­ч­ни­ми зна­чен­ня­ми. Як­що G_р<G_табл, то гі­по­те­за про од­но­рі­д­ність ди­с­пер­сії при­йма­є­ть­ся. У про­ти­в­но­му ви­пад­ку від­хи­ля­є­ть­ся.

Од­но­рі­д­ність ди­с­пер­сії по ряд­ках го­во­рить про те, що в ста­ти­с­ти­ч­них да­них не­має ве­ли­ких си­с­те­ма­ти­ч­них по­ми­лок, тобто усі ви­мі­ри у всіх то­ч­ках про­с­то­ру ма­ють при­бли­з­но ту са­му то­ч­ність.

Етап 4. Пе­ре­вір­ка ста­ти­с­ти­ч­ної зна­чи­мо­с­ті ко­е­фі­ці­є­н­тів рі­в­нян­ня ре­г­ре­сії.

y=b₀+b₁x₁+ b₂x₂+…

Зна­чи­мість екс­пе­ри­мен­ту пе­ре­ві­ря­є­ть­ся за кри­те­рі­єм Стью­ден­та, що об­чи­с­лю­є­ть­ся по фор­му­лі

Роз­ра­хун­ко­ві зна­чен­ня до­рі­в­ню­ю­ть­ся з таб­ли­ч­ни­ми зна­чен­ня­ми, при цьо­му чи­с­ло сту­пе­нів сво­бо­ди до­рі­в­нює

f=N(n-1)

Як­що t_р для ко­е­фі­ці­є­н­тів b_i біль­ше t_табл, то цей ко­е­фі­ці­єнт вва­жа­є­ть­ся ста­ти­с­ти­ч­но зна­чи­мим із ймо­ві­р­ні­с­тю Р=1-. Іна­к­ше цей ко­е­фі­ці­єнт іс­то­т­но не впли­ває на ви­хі­д­ну ве­ли­чи­ну у, тобто зна­хо­ди­ть­ся на рі­в­ні по­хиб­ки і йо­го мо­ж­на ви­клю­чи­ти.

Етап 4. Пе­ре­вір­ка аде­к­ва­т­но­с­ті мо­де­лі.

Во­на ви­ко­ну­є­ть­ся по F-критерію Фі­ше­ра. Роз­ра­хун­ко­ві зна­чен­ня цьо­го кри­те­рію об­чи­с­лю­ю­ть­ся по фор­му­лі

де оцінка дисперсії адекватності моделі.

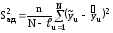
де число значимих коефіцієнтів у рівнянні регресії;

зна­чен­ня ви­хі­д­ної ве­ли­чи­ни в u-ій то­ч­ці, об­чи­с­ле­не по отри­ма­но­му рі­в­нян­ню ре­г­ре­сії

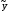=b₀+b₁x₁+ b₂x₂+…

відповідає середньому значенню величини в u-ій точці.

Розрахункове значення F_р дорівнюється з табличним значенням при заданій ,

f₁=N- і f₂=N(n-1)

Як­що F_р < F_табл, то з ймо­ві­р­ні­с­тю Р=1- одер­жу­є­мо ма­те­ма­ти­ч­ну мо­дель (рі­в­нян­ня ре­г­ре­сії), що аде­к­ва­т­но опи­сує до­слі­джу­ва­ний про­цес. Іна­к­ше мо­дель не­аде­к­ва­т­на. То­ді посту­па­ють на­сту­п­ним способом:

1. змінити довірчу ймовірність, тобто ;

2. змі­ни­ти шка­лу ви­хі­д­ної ве­ли­чи­ни у, тобто пре­д­ста­ви­ти ви­хі­д­ну ве­ли­чи­ну, як ­ і т.д.­ і­ по­вт­орити ­усі вищевказані етапи;

3. змі­ни­ти план про­ве­ден­ня екс­пе­ри­мен­ту, про­ве­с­ти до­слі­ди і по­даль­шу об­роб­ка екс­пе­ри­мен­таль­них да­них;

4. змі­ни­ти (зме­н­ши­ти) ін­тер­ва­ли ва­рі­ю­ван­ня фа­к­то­рів х_i, i=1, 2, …, m, і про­ве­с­ти екс­пе­ри­мен­ти з но­ви­ми зна­чен­ня­ми (ета­пи 1-5).

Дробовий факторний експеримент (ДФЕ)

Від­рі­з­ня­є­ть­ся від ПФЕ тим, що до­зво­ляє іс­то­т­но ско­ро­ти­ти кіль­кість до­слі­дів. У те­о­рії пла­ну­ван­ня екс­пе­ри­мен­тів іс­нує мо­ж­ли­вість по­бу­ду­ва­ти пла­ни, що яв­ля­ю­ть­ся ча­с­ти­ною ПФЕ і ма­ють вла­с­ти­во­с­ті ор­то­го­наль­но­го пла­ну­ван­ня. Та­кі екс­пе­ри­мен­ти на­зи­ва­ю­ть­ся дро­бо­ви­ми фа­к­то­р­ни­ми екс­пе­ри­мен­та­ми. Як­що про­во­ди­ть­ся екс­пе­ри­мент, що пре­д­ста­в­ляє по­ло­ви­ну ПФЕ 2ⁿ, тобто кіль­кість до­слі­дів N_д=2^n-1, то він на­зи­ва­є­ть­ся пів­ре­п­лі­кою ПФЕ. Як­що ДФЕ має кіль­кість до­слі­дів N_д=2^n-2, то він на­зи­ва­є­ть­ся че­т­ве­р­ною ре­п­лі­кою ПФЕ. І так да­лі. Будь-­які дро­бо­ві ре­п­лі­ки ма­ють вла­с­ти­во­с­ті ор­то­го­наль­но­го пла­ну­ван­ня. Утво­рю­є­ть­ся план ДФЕ шля­хом по­бу­до­ви пла­ну ПФЕ, але для ме­н­шо­го чи­с­ла фа­к­то­рів, а ре­зуль­тат не­сут­тє­во­го ста­ти­с­ти­ч­но не­зна­ч­ної вза­є­мо­дії фа­к­то­рів за­мі­ня­є­ть­ся ін­ши­ми фа­к­то­ра­ми. Про­це­ду­ру по­бу­до­ви пла­ну ДФЕ роз­г­ля­не­мо на при­кла­ді по­бу­до­ви пів­ре­п­лі­ки від ПФЭ 2⁴, тобто ДФЭ 2^{4 -1}.

u

x0

x1

x2

x3

x4

x1 x2

x1 x3

x1 x4

x2 x3

x2 x4

x3 x4

x1 x2 x3

x1 x2 x4

x2 x3 x4

1

+

+

+

+

+

+

+

2

+

+

+

+

+

+

+

3

+

+

+

+

+

+

+

4

+

+

+

+

+

+

+

5

+

+

+

+

+

+

6

+

+

+

+

+

+

7

+

+

+

+

+

+

8

+

+

+

+

+

+

+

+

+

+

+

+

+

+

x₄= x₁ x₂ x₃

Нехай рівняння регресії для трьох факторів виду

y=b₀+b₁x₁+ b₂x₂+ b₃x₃+ b₁₂x₁x₂+ b₁₃x₁x₃+ b₂₃x₂x₃+ b₁₂₃x₁x₂х₃

Ко­е­фі­ці­єнт b₁₂₃ бу­де ста­ти­с­ти­ч­но не­зна­ч­ний. То­ді пре­д­ста­ви­мо від­су­т­ній фа­к­тор x₄= x₁ x₂ x₃. Про­те ви­ко­ри­с­тан­ня ДФЕ при­зво­дить до ефе­к­ту змі­шу­ван­ня оці­нок ко­е­фі­ці­є­н­та ре­г­ре­сії, що є не­до­лі­ком ДФЕ. Лег­ко ба­чи­ти, що стов­п­чи­ки збі­га­ю­ть­ся. Це ви­кли­ка­но ефе­к­том змі­шу­ван­ня оці­нок ко­е­фі­ці­є­н­тів ре­г­ре­сії. Щоб ви­яви­ти цей ефект, уве­де­ні по­нят­тя спів­від­но­шен­ня, що ге­не­рує, (ГС) і ви­зна­чаль­но­го кон­т­ра­с­ту (ВК).

Спів­від­но­шен­ня, що ге­не­рує, (ГС) - ви­раз, що по­ка­зує за­мі­щен­ням, при вза­є­мо­дії яки­хось фа­к­то­рів уво­ди­ть­ся но­ва змін­на. У на­шім ви­пад­ку ГС бу­де ви­раз x₄= x₁ x₂ x₃. Во­но по­ка­зує, що b₄ яв­ля­є­ть­ся оцін­кою двох ко­е­фі­ці­є­н­тів ₄+₁₂₃. Для ви­зна­чен­ня змі­шан­ня ін­ших оці­нок ви­ко­ри­с­то­ву­є­ть­ся ви­раз, що утво­рю­є­ть­ся шля­хом мно­жен­ня обох ча­с­тин рі­в­но­с­ті ГС на за­мін­ну (х₄), яку ми змін­ю­є­мо.

х₄ х₄= х₁ х₂ х₃ х₄ 1= х₁ х₂ х₃ х₄ – це ВК.

За до­по­мо­гою ВК мо­ж­на ви­зна­чи­ти всі­ля­кі змі­шан­ня оці­нок. Для цьо­го до­ста­т­ньо умно­жи­ти оби­д­ві ча­с­ти­ни рі­в­но­с­ті ВК на змін­ну або до­бу­ток змін­них із від­по­ві­д­ним ко­е­фі­ці­є­н­том.

х₁= х₂ х₃ х₄ b_{1 1}+₂₃₄

х₂= х₁ х₃ х₄ b_{2 2}+₁₃₄

х₁ х₂= х₂ х₃ b_{12 12}+₃₄

Об­чи­с­лен­ня ко­е­фі­ці­є­н­тів при ДФЕ ви­ко­ну­є­ть­ся так са­мо, як і при ПФЕ. Зме­н­шен­ня чи­с­ла до­слі­дів при ДФЕ мо­ж­на ви­ко­на­ти до­ти, по­ки чи­с­ло до­слі­дів не ста­не рі­в­ним чи­с­лу фа­к­то­рів. Та­кий план, у яко­му чи­с­ло до­слі­дів до­рі­в­нює чи­с­лу фа­к­то­рів, на­зи­ва­є­ть­ся на­си­че­ним.