matmodeom / MMM_Lek / U_M_d_2

Формула Симпсона

Цей метод визначення визначеного інтеграла заснований на тому, що на відрізку [x₀,x₀+2h] ду­гу підінтегральної кри­вої за­мі­ня­ють ду­гою ква­д­ра­ти­ч­ної па­ра­бо­ли, що про­хо­дить че­рез точки A(x₀,f(x₀)), B(x₀+h,f(x₀+h)), C(x₀+2h,f(x₀+2h)), тобто у даному випадку ви­ко­ну­є­ть­ся квадратична інтерполяція функції y=f(x). З урахуванням цьо­го за на­бли­же­не значення визначеного інтеграла приймається пло­ща криволінійної трапеції, утвореної віс­сю ОХ, пря­ми­ми х=х₀, х=х₀+2h і квадратичною па­ра­бо­лою.

f(x)

y

квадратна парабола Р₂(х)

C

B

y₁

A

y₂

y₀

x₀ x₀+h x₀+2h x

Відповідно до першої інтерполяційної формули Ньютона:

Перетворимо даний вираз з урахуванням того, що х₁=х₀+h, тоді

(x-x₀)(x-x₁) = (x-x₀)(x-x₀-h) = (x-x₀)²-(x-x₀)h

Представимо отриманий вираз в поліном виді і обчислимо інтеграл

З урахуванням того, що y₀=y₁-y₀ ²y₀=y₂-2y₁+y₀. Позначимо y₀=y_н y₁=y_ср y₂=y_к.

Отри­ма­не ви­раз ви­ко­ри­с­то­ву­є­ть­ся для об­чи­с­лен­ня ви­зна­че­но­го ін­те­г­ра­ла ме­то­дом Си­м­п­со­на. Для цьо­го по­ді­ли­мо від­рі­зок ін­те­г­ру­ван­ня [a,b] на n-рівних ча­с­тин, при­чо­му n=2m, то­ді

Обчислимо значення функції в точках розподілу:

y₀=f(x₀)=f(a)

y₁=f(x₁)

y₂=f(x₂)

…

y_n=f(x_n)=f(b)

Обчислимо площу криволінійної трапеції на відрізках [x₀,x₂], [x₂,x₄],…,[x_n-2,x_n].

Формула Симпсона:

По­хиб­ка об­чи­с­лен­ня ви­зна­че­но­го ін­те­г­ра­ла по фор­му­лі Си­м­п­со­на з те­о­рії об­чи­с­лю­валь­них ме­то­дів до­рі­в­нює:

Для пра­к­ти­ч­них роз­ра­хун­ків мо­ж­на ви­ко­ри­с­то­ву­ва­ти ме­тод Ру­н­ге, від­по­ві­д­но до яко­го:

Як­що підінтегральна фун­к­ція y=f(x) за­да­на в таб­ли­ч­нім ви­ді, то для об­чи­с­лен­ня по­хиб­ки ін­те­г­ру­ван­ня за до­по­мо­гою фор­му­ли Си­м­п­со­на мо­ж­на ско­ри­с­та­ти­ся фор­му­лою:

Чисельні розв'язання

диференціальних рівнянь

Не­об­хід­ність чи­се­ль­но­го роз­в'я­зан­ня ди­фе­ре­н­ці­аль­них рі­в­нянь по­ля­гає в то­му, що кла­си­ч­ні ме­то­ди не­мо­ж­ли­во ре­а­лі­зу­ва­ти на ЕОМ і в той же час важ­ко ви­рі­ши­ти ди­фе­ре­н­ці­аль­ні рі­в­нян­ня в еле­мен­та­р­них фун­к­ці­ях.

Чи­се­ль­ні ме­то­ди до­зво­ля­ють за до­по­мо­гою ЕОМ одер­жа­ти зна­чен­ня фун­к­ції в не­об­хід­них то­ч­ках.

Роз­г­ля­не­мо чи­се­ль­не ди­фе­ре­н­ці­ю­ван­ня пер­шо­го по­ряд­ку ви­ду:

y^I=f(x,y) (1)

За­галь­ним рі­шен­ням да­но­го ди­фе­ре­н­ці­аль­но­го рі­в­нян­ня бу­де сі­мей­с­т­во фун­к­цій y=(x,c), що за­ле­жать від по­хі­д­ної кон­с­тан­ти с. Для то­го, щоб ви­зна­чи­ти зна­чен­ня фун­к­ції в якійсь кон­к­ре­т­ній то­ч­ці х, тре­ба ви­ді­ли­ти з цьо­го сі­мей­с­т­ва окре­ме рі­шен­ня за до­по­мо­гою по­ча­т­ко­вої умо­ви:

(2)

Знаходження рішення диференціального рівняння (1), що задовольняє умову (2), називається задачею Коші.

За­да­ча чи­се­ль­но­го рі­шен­ня ди­фе­ре­н­ці­аль­но­го рі­в­нян­ня по­ля­гає у ви­зна­чен­ні таб­ли­ці y=(x), що за­до­во­ль­няє рі­в­нян­ня (1) і умо­ву (2) у то­ч­ках із кро­ком h на від­різ­ку [a,b]. При цьо­му вва­жа­ють, що

x₀=a

x₁=x₀+h

…

x_n=x₀+nh=b

Метод Эйлера

Цей ме­тод є най­більш про­с­тим. Ви­ко­ри­с­то­ву­є­ть­ся для при­бли­з­них роз­ра­хун­ків, але ідея, за­кла­де­на в ньо­му, є вихідною для ши­ро­ко­го кла­су чи­се­ль­них ме­то­дів роз­в'я­зан­ня ди­фе­ре­н­ці­аль­них рі­в­нянь.

Цей ме­тод ба­зу­є­ть­ся на за­мі­ні шу­ка­ної фун­к­ції ба­га­то­чле­ном 1-ого сту­пе­ня, тобто на лі­ній­ні ін­тер­по­ля­ції, то­ч­ні­ше ек­с­т­ра­по­ля­ції, то­му що ми зна­хо­ди­мо зна­чен­ня фун­к­ції в су­сі­д­ніх ву­з­лах, а не між ни­ми.

Ви­бе­ре­мо де­який крок h, що яв­ляє со­бою ін­тер­вал [a,b], на який ми роз­би­ва­є­мо від­рі­зок. Не­хай h до­ста­т­ньо ма­лий, та­кий, що зна­чен­ня фун­к­ції y=f(x) на ді­ля­н­ці [x₀,x₀+h] ма­ло від­рі­з­ня­є­ть­ся від лі­ній­ної фун­к­ції. За­пи­ше­мо рі­в­нян­ня до­ти­ч­ної в то­ч­ці (х₀,у₀)

Ви­хі­д­на за­да­ча роз­в'я­зан­ня ди­фе­ре­н­ці­аль­них рі­в­нянь фор­му­лю­є­ть­ся ра­ні­ше, то y^I=f(x,y).

x0	x1	x2	x3	…	xn
y0	y1	y2	y3	…	yn

x₀=a x_n=b

Ми д­ер­­жимо ­ріш­ення по ­ме­тоду ­Эй­лера. Г­ео­м­ет­р­ично ­ріш­ення ­Коші ­ме­тодом ­Эй­лера п­р­едс­т­ав­л­яю­ться:

(y_n)

y

x₀ x₁ x_n-1 x_n x

По­хиб­ка ме­то­дом Эй­ле­ра за­ле­жить від ве­ли­чи­ни кро­ку h: чим ме­н­ше крок, тим ви­ще то­ч­ність роз­в'я­зан­ня за­да­чі. Для оці­ню­ван­ня то­ч­но­с­ті ви­ко­ри­с­то­ву­є­ть­ся на­сту­п­на фор­му­ла:

y_n – значення функції наприкінці інтервалу пошуку рішення задачі з кроком h,

– зна­чен­ня фун­к­ції на­при­кі­н­ці ін­тер­ва­лу по­шу­ку рі­шен­ня за­да­чі з кро­ком 2h.

Розв'язання системи диференціальних рівнянь

I-го порядку

Нехай дана система диференціальних рівнянь:

(1)

при початкових умовах:

(2)

По­трі­б­но знайти фун­к­ції, що є рі­шен­ням си­с­те­ми (1) при умо­вах (2). Для зна­хо­джен­ня рі­шен­ня ці­єї си­с­те­ми мо­ж­на ви­ко­ри­с­то­ву­ва­ти ті ж ме­то­ди, що і для роз­в'я­зан­ня од­но­го рі­в­нян­ня.

t₁=t₀+h, де h – величина кроку розбивки відрізка [a,b].

x₁=x₀+f₁(x₀,y₀,t₀)h y₁=y₀+f₁(x₀,y₀,t₀)h

x₂=x₁+f₂(x₁,y₁,t₁)h y₂=y₁+f₂(x₁,y₁,t₁)h

……………… ………………

x_n=x_n-1+f_n(x_n-1,y_n-1,t_n-1)h y_n=y_n-1+f_n(x_n-1,y_n-1,t_n-1)h

Таким чином, ми одержуємо таблицю:

t	t0	t1	t2	…	tn
x	x0	x1	x2	…	xn
y	y0	y1	y2	…	yn

Розв'язання системи диференціальних рівнянь

вищих порядків

Нехай необхідно розв'язати диференціальні рівняння:

y^II=f(x,y,y^I) (1)

при початкових умовах:

Для роз­в'я­зан­ня поста­в­ле­ної за­да­чі зро­би­мо за­мі­ну змін­них: z=y^I, z^I=y^II, то­ді ви­хі­д­не рі­в­нян­ня (1) бу­де яв­ля­ти со­бою си­с­те­му:

Роз­в'я­зан­ня да­ної за­да­чі ви­ко­ну­є­ть­ся будь-­яким із ві­до­мих ме­то­дів, на­при­к­лад, ме­то­дом Эй­ле­ра, що був опи­са­ний ра­ні­ше.

Та­ким чи­ном, роз­в'я­зан­ня ди­фе­ре­н­ці­аль­них рі­в­нянь ви­щих по­ряд­ків ви­ко­ну­є­ть­ся шля­хом їх­ньо­го пре­д­ста­в­лен­ня (за­мі­ни) си­с­те­мою ди­фе­ре­н­ці­аль­них рі­в­нянь.

Модифікований метод Эйлера

Цей ме­тод ви­ко­ри­с­то­ву­є­ть­ся для роз­в'я­зан­ня ди­фе­ре­н­ці­аль­но­го рі­в­нян­ня I-го по­ряд­ку і пра­к­ти­ч­но в то­му ж об­ся­зі об­чи­с­лень до­зво­ляє одер­жа­ти більш ви­со­ку то­ч­ність по­ряд­ку h² за­мість h у ме­то­ді Эй­ле­ра. По­ка­же­мо су­т­ність ко­ж­но­го ме­то­ду на од­но­му ча­с­т­ко­во­му ін­тер­ва­лі [x₀,x₀+h].

y

C

B

C₁

А

x₀ x₀+h x

Знайдемо дотичну в точці В. Кут нахилу буде дорівнювати:

, у₁=у₀+h.

Та­ким чи­ном, ал­го­ритм мо­ди­фі­ко­ва­но­го ме­то­ду Эй­ле­ра бу­де скла­да­ти­ся з ета­пів:

1. обчислюємо ;

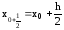2. знаходимо ;

3. обчислимо кут нахилу дотичної до точки з координатами

4. обчислюємо значення функції у₁=у₀+h.

Метод Эйлера-Коши

Кут на­хи­лу до­ти­ч­ної або ла­ма­ної лі­нії ви­зна­ча­є­ть­ся як се­ре­д­нє зна­чен­ня до­ти­ч­ної в по­ча­т­ко­вій і кі­н­це­вій то­ч­ках.

y

В

₁

y=f(x)

С

₂

А

x₀ x₀+h x

Алгоритм розв'язання даного методу:

1. визначаємо кут нахилу дотичної в початковій точці А

₁=f(x₀,y₀);

2. визначаємо точку пересічення прямої із даною дотичною, з прямою х₀+h

;

3. визначаємо ₂ у точці В

4. визначаємо кут

;

5. визначаємо у₁=у₀+h.

Да­на по­слі­до­в­ність по­вто­рю­є­ть­ся n ра­зом.

По­хиб­ка да­но­го ме­то­ду, як і мо­ди­фі­ко­ва­но­го ме­то­ду Эй­ле­ра, має ква­д­ра­ти­ч­ну за­ле­ж­ність від h. По­хиб­ка об­чи­с­лю­є­ть­ся по фор­му­лі: