Обчислення похідної другої інтерполяційної формули Ньютона

Ця формула для обчислення похідною у вузлах інтерполяції з використанням 2-ої інтерполяційної формули

На пра­к­ти­ці зру­ч­но ви­ко­ри­с­то­ву­ва­ти та­кі фор­му­ли чи­се­ль­но­го ди­фе­ре­н­ці­ю­ван­ня для будь-­яко­го вну­т­рі­ш­ньо­го ву­з­ла x_i:

При наявності 3-х вузлів

З на­ве­де­них фор­мул оче­ви­д­но, що зі зме­н­шен­ням кро­ку h або зі збіль­шен­ням n, по­грі­ш­ність ди­фе­ре­н­ці­ю­ван­ня зме­н­шу­є­ть­ся. Зна­ю­чи по­грі­ш­ність ме­то­ду і по­ми­л­ку, що ви­кли­кає по­грі­ш­ність ви­хі­д­них да­них, мо­ж­на ви­зна­чи­ти оп­ти­маль­ний роз­мір кро­ку h при за­да­ній ма­к­си­маль­ній і до­пу­с­ти­мій по­грі­ш­но­с­ті:

При обчисленні 2-ої похідної

Чисельне інтегрування функцій

Не­хай фун­к­ція f(x) за­да­на на від­різ­ку [a,b]. роз­г­ля­не­мо фор­му­лу об­чи­с­лен­ня ви­зна­че­но­го ін­те­г­ра­лу .Як­що для ці­єї фун­к­ції ві­до­ма пер­ві­с­на F(x), то ви­ко­ри­с­то­ву­є­мо фор­му­лу Нью­то­на-­Лей­б­ні­ца:

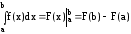
Про­те пер­ві­с­на мо­же бу­ти отри­ма­на тіль­ки для ву­зь­ко­го кла­су фун­к­цій, при­чо­му її опис по­в'я­за­ний із до­ста­т­ньо гро­мі­з­д­ки­ми об­чи­с­лен­ня­ми, крім то­го, пі­ді­нте­г­раль­на фун­к­ція f(x) мо­же бу­ти за­да­на не в ана­лі­ти­ч­но­му ви­гля­ді, а в таб­ли­ч­но­му або гра­фі­ч­но­му. То­му при­хо­ди­ть­ся ви­ко­ри­с­то­ву­ва­ти рі­з­но­ма­ні­т­ні на­бли­же­ні фор­му­ли. До­ста­т­ньо про­с­то ці фор­му­ли одер­жа­ти, ви­хо­дя­чи з гео­ме­т­ри­ч­но­го зна­чен­ня ви­зна­че­но­го ін­те­г­ра­лу. Як­що фун­к­ція f(x) 0 на від­різ­ку [a,b], то

f(x)

y

S

S_n

a b x

Для на­бли­же­но­го об­чи­с­лен­ня пло­щі кри­во­лі­ній­ної тра­пе­ції за­мі­ня­ють її пло­щею більш про­с­тої фі­гу­ри.

У за­ле­ж­но­с­ті від то­го, яким спо­со­бом ми за­мі­ня­є­мо пло­щу кри­во­лі­ній­ної тра­пе­ції, за­сто­со­ву­ють на­сту­п­ні ме­то­ди об­чи­с­лен­ня ви­зна­че­но­го ін­те­г­ра­ла:

1. метод прямокутників ( лівих, правих, середніх);

2. метод трапецій;

3. метод криволінійних трапецій (метод Симпсона).

Формула прямокутників

Ідея цих фор­мул скла­да­є­ть­ся в то­му, що на де­яко­му ма­лень­ко­му від­різ­ку пло­ща кри­во­лі­ній­ної тра­пе­ції за­мі­ня­ється пло­щею пря­мо­ку­т­ни­ка з під­ста­вою [x₀,x₀+h] і ви­со­тою, рі­в­ною зна­чен­ню фун­к­ції на цьо­му ін­тер­валі.

y

x₀ h x₀+h x

f(), [x₀,x₀+h]

У за­ле­ж­но­с­ті від то­го, яку то­ч­ку ви­би­ра­є­мо у яко­с­ті , одер­жу­є­мо ту або ін­шу фор­му­лу пря­мо­ку­т­ни­ка.

Не­хай не­об­хід­но знайти зна­чен­ня ви­зна­че­но­го ін­те­г­ра­ла. Роз­ді­ли­мо ін­тер­вал на n рі­в­них ча­с­тин.

f(x)

y

S_n

a=x₀ b=x_n x

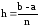
x₀=a y₀=f(x₀)

x₁=x₀+h y₁=f(x₁)

x₂=x₁+h y₂=f(x₂)

На кожному інтервалі в якості ординати беремо значення функції в лівому кінці відрізка.

Як­що у яко­с­ті ор­ди­на­ти ви­би­ра­є­мо зна­чен­ня фун­к­ції з пра­во­го краю від­різ­ка, то одер­жу­є­мо фор­му­лу пра­вих пря­мо­ку­т­ни­ків.

f(x)

y

S_n

x

Як­що для об­чи­с­лен­ня пло­щі пря­мо­ку­т­ни­ка ви­би­ра­є­ть­ся се­ре­д­ня то­ч­ка ко­ж­но­го ча­с­т­ко­во­го від­різ­ка , тобто

y

f(x)

S_n

x

Отри­ма­ні фор­му­ли мо­ж­на ви­ко­ри­с­то­ву­ва­ти та­кож для ви­пад­ку ву­з­лів, що зна­хо­дя­ть­ся на рі­з­ній від­ста­ні один від од­но­го. Не­хай ві­до­мі зна­чен­ня фун­к­ції.

x	x0	x1	x2	x3	…	xn
y	y0	y1	y2	y3	…	yn

x₀=a x_n=b h₁=x₁-x₀

h₁=x₁-x₀

h₂=x₂-x₁

…

h_n=x_n-x_n-1

Тоді формула лівих прямокутників набуває вигляду :

Як­що зна­чен­ня фун­к­ції ви­би­ра­є­ть­ся в ко­ж­но­му пра­во­му кі­н­ці ча­с­ти­ни від­різ­ка, то фор­му­ла пра­во­го пря­мо­ку­т­ни­ка на­бу­ває ви­гля­ду: