Сиплекс метод розв'язання задач лінійного програмування

Цей ме­тод ви­ко­ри­с­то­ву­є­ть­ся для роз­в'я­зан­ня та­ких за­дач. Знайти n змін­них х₁, х₂, …, х_n, поста­ча­ю­чих ма­к­си­мум (мі­ні­мум) ці­льо­вої фун­к­ції

,

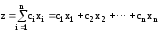на область визначення якої накладається обмеження

По­ка­же­мо роз­в'я­зан­ня да­ної за­да­чі гра­фі­ч­но. Тре­ба знайти зна­чен­ня х₁, х₂, для яких ці­льо­ва фун­к­ція бу­де ма­ти ма­к­си­маль­не зна­чен­ня при умо­вах:

max z=10x₁+15x₂

0,5x₁+2,5x₂50 x₁0 x₂0

3x₁+x₂120

y

120

80

60

40

20

20 40 60 80 100 x

Нехай z₁=450, z₂=300.

Тобто шу­ка­не рі­шен­ня зна­хо­ди­ть­ся у вер­ши­ні ба­га­то­гран­ни­ка (си­п­ле­к­са), утво­ре­но­го об­ме­жен­ня­ми за­дач.

При роз­в'я­зан­ні за­дач лі­ній­но­го про­гра­му­ван­ня об­ласть до­пу­с­ти­мих рі­шень мо­же бу­ти:

1. порожньою, на практиці ця задача не має сенсу;

2. область являє собою опуклий багатогранник;

3. опу­к­лий ба­га­то­гран­ник, що іде од­ні­єю з гра­ней у не­скін­чен­ність, має мі­с­це без­кі­не­ч­на мно­жи­на рі­шень.

Те­о­ре­ма лі­ній­но­го про­гра­му­ван­ня ви­зна­чає ви­гляд об­ла­с­ті, до­зво­ляє ви­зна­чи­ти од­не з до­пу­с­ти­мих рі­шень, уста­но­ви­ти чи є рі­шен­ня оп­ти­маль­ним, а як­що ні, то знайти на­сту­п­ну то­ч­ку, най­бли­ж­чу до оп­ти­маль­ної (ука­зує шлях зна­хо­джен­ня оп­ти­му­му).

Основні положення сиплекса-методу

1. Будь-­яку си­с­те­му лі­ній­них не­рі­в­но­с­тей, що ви­зна­чає об­ласть до­пу­с­ти­мих рі­шень за­да­чі лі­ній­но­го про­гра­му­ван­ня, мо­ж­на за­мі­ни­ти ек­ві­ва­лен­т­ною їй си­с­те­мою рі­в­нянь, ви­ко­нав де­які фор­маль­ні пе­ре­тво­рен­ня.

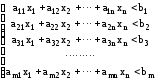
За­мі­ни­мо цю си­с­те­му не­рі­в­но­с­тей рі­в­но­с­тя­ми, уві­в­ши до­да­т­ко­ві змін­ні х_n+1, х_n+2, …, х_n+m.

2. Не­хай ма­є­мо си­с­те­му m рі­в­нянь із n не­ві­до­ми­ми. При цьо­му вва­жа­є­мо, що m<n. По­ді­ли­мо цю си­с­те­му на дві ча­с­ти­ни, у ко­т­рій пер­ші m змін­них бу­дуть ос­но­в­ни­ми,

а ін­ші не ос­но­в­ни­ми. Усі не ос­но­в­ні змін­ні пе­ре­не­се­мо в пра­ву ча­с­ти­ну рі­в­нянь.

Полученную систему можно решить относительно переменных х₁, х₂, …, х_m, если присвоить не основным переменным произвольные значения. Количество решений бесконечно, но если присвоить не основным переменным нулевые значения, то решение будет единственным. Выбранные основные переменные представляют собой базисное решение задачи линейного программирования.

3. Ви­ще­вка­за­ну си­с­те­му рі­в­нянь мо­ж­на най­про­с­ті­ши­ми пе­ре­тво­рен­ня­ми при­ве­с­ти до ка­но­ні­ч­но­го ви­ду, де в лі­вій ча­с­ти­ні бу­де­мо иметь оди­ни­ч­ну ма­т­ри­цу.

х₁ =b₁ ( )

х₂ =b₂ ( )

…

х_m=b_m ( )

Та­ким чи­ном, від­по­ві­д­но до п.1, у ко­т­ро­му, уві­в­ши до­да­т­ко­ві змін­ні х_n+1, х_n+2, …, х_n+m, ми одер­жа­ли ка­но­ні­ч­ну фор­му за­пи­су си­с­те­ми рі­в­нянь, у ко­т­рій вве­де­ні змін­ні х_n+1, х_n+2, …, х_n+m утво­рять ба­зи­с­не рі­шен­ня, що є пер­шим до­пу­с­ти­мим рі­шен­ням за­да­чі лі­ній­но­го про­гра­му­ван­ня. Ці вве­де­ні змін­ні на­зи­ва­ю­ть­ся шту­ч­ни­ми змін­ни­ми.

З ура­ху­ван­ням ви­ще­ви­кла­де­них по­ло­жень роз­г­ля­не­мо су­т­ність си­п­ле­к­са-­ме­то­ду роз­в'я­зан­ня за­да­чі лі­ній­но­го про­гра­му­ван­ня.