matmodeom / MMM_Lek / U_M_d_3

Метод Рунге-Кутта

Це най­біль­ше ча­с­то ви­ко­ри­с­то­ву­ва­ний ме­тод при чи­се­ль­но­му роз­в'я­зан­ні за­да­чі Ко­ші, то­му що до­зво­ляє одер­жа­ти на­бли­же­не рі­шен­ня з ве­ли­кою то­ч­ні­с­тю.

Не­хай не­об­хід­но ви­рі­ши­ти ди­фе­ре­н­ці­аль­не рі­в­нян­ня у^I=f(x,y) при по­ча­т­ко­вих умо­вах у(х=х₀)=у₀ на від­різ­ку [a,b]. Ро­зі­б'є­мо ін­тер­вал ін­те­г­ру­ван­ня на n рі­в­них ча­с­тин.

x₀=a x_n=b

x₁=x₀+h

x₁=x₁+h=x₀+2h

…

x_n=x₀+nh

По­ка­же­мо су­т­ність ме­то­ду для пер­шо­го ін­тер­ва­лу [x₀,x₁]. З то­ч­ки М₀(х₀,у₀) про­ве­де­мо до­ти­ч­ну до кри­вої у=f(х). Рі­в­нян­ня до­ти­ч­ної бу­де ма­ти вид:

у-у₀=f ^I(x₀,y₀)(x-x₀)

у-у₀=₁₀(x-x₀) ₁₀=f(x₀,y₀)

Знайдемо точку пересічення дотичної і прямої це буде точка . Знайдемо кут нахилу дотичної до кривої в цій точці.

1

y

2

45

3

M₁

M₀

x₀ 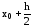x₀+h x

З точки М₀ проведемо пряму з цим кутом нахилу.

y-у₀ =₂₀(х-х₀)

Знайде­мо то­ч­ку пе­ре­сі­чен­ня ці­єї пря­мої з пря­мої 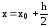. ­Це­ ­бу­де точка .­ Обчи­сл­и­мо кут на­хи­л­у до­тичної ­до інтег­рально­ї­ кривої в даній точці

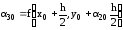
Проведемо пряму з даним кутом нахилу з точки М₀. Рівняння прямої:

у-у₀=₃₀(х-х₀)

Пе­ре­сі­чен­ня ці­єї пря­мої з пря­мої х=х₀+h – це то­ч­ка ­(­x­₀+­h,y₀+₃₀h­).­ Обчи­сл­и­мо кут на­хи­л­у до­тичної ­до інтег­рально­ї­ кривої в даній точці

Обчислимо середній кут нахилу ₀:

Про­ве­де­мо до­ти­ч­ну до ін­те­г­раль­ної кри­вої до то­ч­ки M з точк­и­ М₀. ­То­чк­а М­₁ – т­очка п­ересіченн­я цієї прямої ­з пря­мо­ї­ х­=х₀+h­. ­Вона являється шуканою.

у-у₀=₀(x-x₀)

у₁=у₀+₀h

у₂=у₁+₁h

Таким чином, алгоритм розв'язання полягає в наступному:

1. розіб'ємо відрізок [a,b] n рівних частин;

2. для першого інтервалу [x₀,x₀+h] обчислимо кути нахилу

₁₀=f(x₀,y₀)

;

3. визначимо середній кут нахилу ₀

;

4. обчислимо значення шуканої функції в точці х₁=х₀+h.

Повторимо пункти 2,3,4 для інших підінтервалів.

k=1,2,…,h.

При тій са­мій кіль­ко­с­ті роз­би­вок ін­тер­ва­лу ме­тод Ру­н­геКут­та до­зво­ляє одер­жа­ти більш ви­со­ку то­ч­ність у по­рі­в­нян­ні з ра­ніш роз­г­ля­ну­ти­ми ме­то­да­ми, або для до­ся­г­нен­ня од­ні­єї й ті­єї ж то­ч­но­с­ті зме­н­ши­ти кіль­кість роз­би­вок.

Ме­тод Ру­н­геКут­та має 4-й по­ря­док то­ч­но­с­ті від кро­ку роз­бив­ки h. Чим ме­н­ше крок h, тим біль­ше то­ч­ність у сту­пе­ні h⁴, і на­в­па­ки. Для пра­к­ти­ч­них об­чи­с­лень по­хиб­ку в остан­ній n то­ч­ці мо­ж­на одер­жа­ти

де y_n – значення функції в точці x_n при кількості розбивок n,

– значення функції в точці x_n при кількості розбивок 2n.

Багатокрокові методи розв'язання

диференціальних рівнянь

У ра­ні­ше роз­г­ля­ну­тих ме­то­дах на ко­ж­но­му кро­ку об­чи­с­лень ви­ко­ри­с­то­ву­є­ть­ся ін­фор­ма­ція про зна­чен­ня шу­ка­но­го роз­в'яз­ку в од­ній по­пе­ре­дній то­ч­ці. Іс­нує ряд ме­то­дів, що до­зво­ля­ють одер­жа­ти рі­шен­ня з ве­ли­кою то­ч­ні­с­тю, ви­ко­ри­с­то­ву­ю­чи рі­шен­ня в де­кіль­кох то­ч­ках, ра­ні­ше отри­ма­них. Ці ме­то­ди на­зи­ва­ю­ть­ся ба­га­то­кро­ко­ви­ми. Се­ред них най­біль­ше ча­с­то ви­ко­ри­с­то­ву­ю­ть­ся ме­то­ди Ада­м­са. Су­т­ність цих ме­то­дів по­ля­гає в на­сту­п­но­му. Не­хай знайде­ні при­бли­з­ні рі­шен­ня фун­к­ції в(х) у (k+1) то­ч­ці, тобто в то­ч­ках x_i, x_i-1, x_i-2, …, x_i-k ві­до­мі у_i, у_i-1, у_i-2, …, у_i-k. Для одер­жан­ня фун­к­ції за да­ни­ми то­ч­ка­ми по­бу­ду­є­мо ін­тер­по­ля­цій­ний по­лі­ном Р_k(x). Бу­де­мо вва­жа­ти, що у^I=P_k(x,y). То­ді

Ви­ко­ри­с­то­ву­ю­чи ін­тер­по­ля­цій­ну фор­му­лу Нью­то­на (ін­тер­по­ля­ція то­му) і об­ме­жу­ю­чись рі­з­ни­ця­ми 3-го по­ряд­ку, мо­ж­на одер­жа­ти ек­с­т­ра­по­ля­цій­ну фор­му­лу Ада­м­са

F_i=hf(x_i,y(x_i))

Формула Адамса - Башфорта

Якщо у формулі різниці представити у вигляді виразів:

F_i-1=h(f_i-f_i-1)

²F_i-2=h(f_i-2f_i-1+f_i-2)

³F_i-1=h(f_i-3f_i-1+3f_i-2-f_i-3),

то одержимо формула Адамса Башфорта:

f_i=f(x_i,y_i)

Формула Адамса Мултона

Після обчислень y_i+1 по формулі Адамса з початку визначається

f_i+1=f(x_i+1,y_i+1),

а потім y_i+1 уточнюється по формулі

Це фор­му­ла Ада­м­са Му­л­то­на. Для оці­ню­ван­ня по­хиб­ки ме­то­ду Ада­м­са Му­л­то­на мо­ж­на ви­ко­ри­с­то­ву­ва­ти фор­му­лу:

Метод Мілна

Цей ме­тод є ба­га­то­кро­ко­вим із 4-м по­ряд­ком то­ч­но­с­ті ти­пу про­ро­ку­ван­ня - ко­ре­к­ція. Для йо­го ро­бо­ти не­об­хід­но яки­мось од­но­кро­ко­вим ме­то­дом знайти по­пе­ре­днє зна­чен­ня у₀, у₁, у₂, у₃ у то­ч­ках х₀, х₁, х₂, х₃. По­тім по цих то­ч­ках тре­ба об­чи­с­ли­ти по­пе­ре­дньо зна­чен­ня

i= 3, 4, 5, …

f_i=f(x_i,y_i)

Потім обчислюється

Далі відбувається коректування y_i+1

Дана послідовність у^попер. і у^кор. повторюється для усіх n точок інтервалу. Гранична абсолютна похибка значення y_i визначається по формулі: