Інтерполяція сплайнами

Ра­ніш роз­г­ля­ну­ті ін­тер­по­ля­цій­ні фор­му­ли Нью­то­на і Ла­г­ра­н­жа з ви­ко­ри­с­тан­ням ве­ли­ко­го чи­с­ла ву­з­лів ча­с­то при­зво­дять до по­га­но­го на­бли­жен­ня фун­к­ції, що при­зво­дить до ве­ли­ких на­ко­пи­чень по­хиб­ки в про­це­сі об­чи­с­лен­ня. Крім то­го, че­рез розбіжності про­це­су ін­тер­по­ля­ції збіль­шен­ня чи­с­ла ву­з­лів нео­бо­в’яз­ко­во при­зво­дить до під­ви­щен­ня то­ч­но­с­ті. То­му для то­го, щоб уни­к­ну­ти ве­ли­ких по­хи­бок, весь від­рі­зок [a,b] роз­би­ва­ють на ча­с­т­ко­ві від­різ­ки і на ко­ж­но­му з них при­бли­з­но за­мі­ня­ють ви­хі­д­ну фун­к­цію f(x) ба­га­то­чле­ном не­ви­со­ко­го сту­пе­ня, тобто тут ви­ко­ну­є­ть­ся, так на­зва­на, ку­с­ко­во-­по­лі­но­мі­аль­на ін­тер­по­ля­ція.

Най­біль­ше по­ши­ре­ним за­со­бом та­кої ін­тер­по­ля­ції є ін­тер­по­ля­ція за до­по­мо­гою сплайн-­фун­к­цій.

Сплайн-­фун­к­ці­єю на­зи­ва­ють ку­с­ко­во-­по­лі­но­мі­аль­ну фун­к­цію, що ви­зна­ча­є­ть­ся на про­між­ку [a,b] і має на ньо­му де­яке чи­с­ло не­пе­рерв­них по­хі­д­них.

Пе­ре­ва­гою сплай­нів пе­ред зви­чай­ною ін­тер­по­ля­ці­єю є:

1. збіжність;

2. сталість процесу обчислення.

Роз­ди­ви­мо­ся окре­мі ви­пад­ки сплайн-­фун­к­ції, ко­ли на ко­ж­но­му ча­с­т­ко­во­му від­різ­ку во­на зо­бра­жу­є­ть­ся у ви­ді ба­га­то­чле­на 3-ого сту­пе­ня. У та­кий спо­сіб ми одер­жу­є­мо ку­бі­ч­ний сплайн.

Не­хай на від­різ­ку [a,b] за­да­на не­пе­рерв­на фун­к­ція f(x), у ву­з­лах ко­т­рої a = x₀, x₁, x₂, …, x_n = b, при­чо­му, х₀ < x₁ < x₂ < … < x_n. По­зна­чи­мо зна­чен­ня фун­к­ції f_i = f(x_i), i = 0, 1, 2, …, n.

Сплайном, що відповідає функції f(x) у вузлах , називається функція S(x), що задовольняє вимогам:

1. на кожному окремому відрізку [x_i-1,x_i], i = 1, 2, …, n, є багаточленом 3-ого ступеня;

2. функція S(x) і її 1, 2-га похідні неперервні на відрізку [a,b];

3. сплайн і зна­чен­ня фун­к­ції збі­га­ю­ть­ся S(x_i) = f(x_i), i = 0, 1, 2, …, n, у ву­з­лах ін­тер­по­ля­ції.

Для по­бу­до­ви сплайн-­фун­к­ції на ко­ж­но­му з окре­мих від­різ­ків [x_i-1,x_i], i = 1, 2, …, n, ми будемо будувати функцію

, х_i-1  x  x_i

де a_i, b_i, c_i, d_i – коефіцієнти, які підлягають визначенню на кожному інтервалі.

Зміст цих ко­е­фі­ці­є­н­тів ви­зна­чим, ви­ра­ху­ва­в­ши 1, 2, 3 по­хі­д­ні цьо­го ба­га­то­чле­на.

З ура­ху­ван­ням цьо­го, а та­кож ви­мог без­пе­рер­в­но­с­ті сплайн-­фун­к­ції S(x), отри­ма­ні та­кі фор­му­ли для об­чи­с­лен­ня не­ві­до­мих ко­е­фі­ці­є­н­тів сплай­нів.

, i=1, 2, …, n-1

h_i=x_i-x_i-1

Це за­пи­са­но си­с­те­му то­ч­них лі­ній­них рі­в­нянь, ко­е­фі­ці­є­н­ти яких яв­ля­ють со­бою лі­ній­ну ма­т­ри­цю, то­му що с₀=с_n=0. Ви­рі­шу­ю­чи си­с­те­му лі­ній­них рі­в­нянь із n-невідомими, одер­жу­є­мо ко­е­фі­ці­є­н­ти c_i, що ви­ко­ри­с­то­ву­ю­ть­ся для ви­зна­чен­ня ко­е­фі­ці­є­н­тів b_i,d_i.

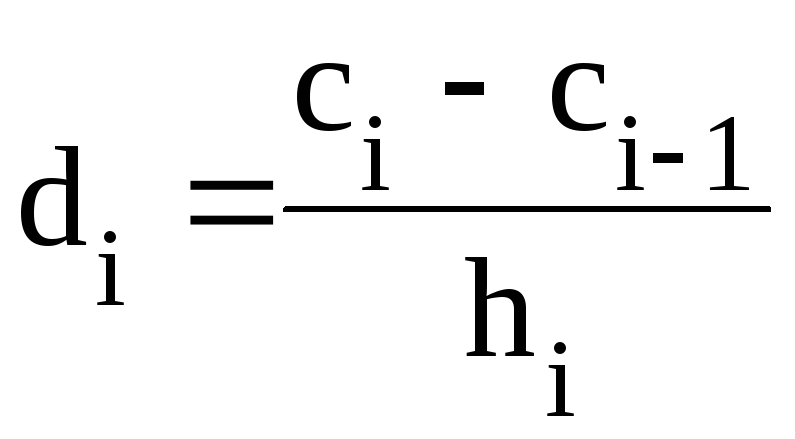, , i=1,2,…,n

a_i=f(x_i), i=0,1,2,…,n

Для оцінки похибки обчислення функцій за допомогою кубічних сплайнов можна скористатися формулами:

a  x  b

Для ви­зна­чен­ня ку­бі­ч­но­го сплай­ну мо­ж­на ско­ри­с­та­ти­ся ін­ши­ми фор­му­ла­ми. Не­хай ви­хі­д­на фун­к­ція f(x) зо­бра­жу­є­ть­ся на ко­ж­но­му при­ва­т­но­му від­різ­ку у ви­ді ку­бі­ч­них ба­га­то­чле­нів

g_i(x)=k_1i +k_2ix+k_3ix²+k_4ix³ i=1,2,3,…,n

g₁(x) g₂(x) g_n(x)

x_n x

x₁

x₀

f(x)

Для зна­хо­джен­ня не­ві­до­мих ко­е­фі­ці­є­н­тів k_1i, k_2i, k_3i, k_4i, тобто їх 4-n штук не­об­хід­но скла­с­ти і ви­рі­ши­ти си­с­те­му рі­в­нянь