
5ДУ
.doc
4.Пример решения варианта типового расчета
Задача 26.
Найти общий интеграл дифференциального
уравнения
 .
.
Данное уравнение является уравнением с разделяющимися переменными
Тогда
![]() ,
,
![]() .
Заметим, что
.
Заметим, что
![]() .
Разделяем переменные:
.
Разделяем переменные:
![]() .
.
Интегрируя правую и левую части, получаем
![]() .
.
После вычисления
интегралов имеем:
![]() .
.
Ответ:
![]() .
.
Задача 27. .Найти общий интеграл дифференциального уравнения
 .
.
Данное уравнение
является однородным. Будем искать
неизвестную функцию
![]() в виде
в виде
![]() .
Тогда
.
Тогда
![]() .
Подставляя
.
Подставляя
![]() и
и
![]() в
исходное уравнение, получаем:
в
исходное уравнение, получаем:

 .
.
Полученное уравнение преобразуем к виду
 .
.
Разделяем переменные
 .
.
Интегрируем правую и левую части
 +
+![]() .
.
(В нашем случае
произвольную постоянную удобнее
обозначит не С, а
![]() ,
где
,
где
![]() .
Вычисляя интегралы в правой и левой
частях уравнения, получаем
.
Вычисляя интегралы в правой и левой
частях уравнения, получаем
![]() .
.
Потенцируя, имеем
![]() .
.
Избавляясь от знака модуля, получаем
![]() .
.
Поскольку
 ,
то полученное соотношение может быть
представлено в виде
,
то полученное соотношение может быть
представлено в виде
 .
.
Данное выражение преобразуем к виду
![]()
Заметим, что в
уравнении
 ,
выражение
,
выражение
 при
при
![]() .
Следовательно, функция
.
Следовательно, функция
![]() является решением дифференциального
уравнения для неизвестной функции
является решением дифференциального
уравнения для неизвестной функции
![]() ,
а значит, функция
,
а значит, функция
![]() является решением исходного
дифференциального уравнения.
является решением исходного
дифференциального уравнения.
Решение
![]() содержится
в решении
содержится
в решении
![]() ,
если положить С=0.
,
если положить С=0.
Ответ:
![]() ,
где С – произвольная постоянная.
,
где С – произвольная постоянная.
Задача 28. Найти решение дифференциального уравнения
![]() ,
,
удовлетворяющее начальному условию y(0)=1.
Вначале найдем
общее решение этого уравнения. Будем
искать
![]() в виде
в виде
![]() .
Тогда
.
Тогда
![]()
![]() =
=![]() .
Подставляя
.
Подставляя
![]() и
и
![]() в исходное уравнение, получаем:
в исходное уравнение, получаем:
![]() +
+![]() ;
;
![]() .
.
Выберем функцию
![]() из условия
из условия
![]() .
Уравнение для функции
.
Уравнение для функции
![]() является уравнением с разделяющимися
переменными. Найдем его решение:
является уравнением с разделяющимися
переменными. Найдем его решение:
![]() ,
,
 ;
;
 ;
;
![]() ;
;
![]() .
.
Найдем функцию
![]() :
:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Тогда общее решение исходного уравнения имеет вид
![]() .
.
Произвольную
постоянную С определим из условия
![]() :
:
![]() .
.
Ответ:
![]() .
.
Задача 29..Найти решение дифференциального уравнения
 ,
удовлетворяющее начальному условию
y(0)=2.
,
удовлетворяющее начальному условию
y(0)=2.
Данное уравнение
является уравнением Бернулли. Будем
искать
![]() в виде
в виде
![]() .
Тогда, подставляя
.
Тогда, подставляя
![]() и
и
![]() в
исходное уравнение, получим
в
исходное уравнение, получим
 :.
Функцию
:.
Функцию
![]() определяем из условия:
определяем из условия:
 ;
;
 ;
;
 ;
;
![]() ;
;
![]() .
Определим
.
Определим
![]() :
:
 ;
;
 ;
;
 +С;
+С;
 ;
;
 .
.
Следовательно,
общее решение имеет вид
 .
Из условия
.
Из условия
![]() определяем произвольную постоянную С:
определяем произвольную постоянную С:
 ;
С=0.
;
С=0.
Ответ:
![]() .
.
Задача 30..Найти
общее решение дифференциального
уравнения
 .
.
Это уравнение явно
не содержит y
. Обозначим
![]() .
Тогда:
.
Тогда:
![]() .
Подставляя в исходное уравнение, получаем
.
Подставляя в исходное уравнение, получаем
 .
.
Уравнение для
определения функции
![]() линейным дифференциальным уравнением
первого порядка. Будем искать
линейным дифференциальным уравнением
первого порядка. Будем искать
![]() в виде
в виде
![]() .
Тогда
.
Тогда
![]()
![]() =
=![]() .
Подставляя
.
Подставляя
![]() и
и
![]() в исходное уравнение, получаем:
в исходное уравнение, получаем:
![]() +
+ ;
;
 .
.
Выберем функцию
![]() из условия
из условия
 .
Уравнение для функции
.
Уравнение для функции
![]() является уравнением с разделяющимися
переменными. Найдем его решение:
является уравнением с разделяющимися
переменными. Найдем его решение:
 ,
,
 ;
;
 ;
;
![]() ;
;
![]() .
.
Найдем функцию
![]() :
:
 ;
;
 ;
;
 ;
;
 .
.
Тогда для функции
![]() имеем выражение
имеем выражение
 .
.
Так как
![]() ,
то
,
то
![]() =
= .,
где
.,
где
![]() - произвольные постоянные.
- произвольные постоянные.
Задача 31. Найти решение дифференциального уравнения
![]() ,
,
удовлетворяющее
начальным условиям y(0)=![]() ,
,
 .
.
Так как исходное
уравнение явно не содержит независимую
переменную
![]() ,
будем искать
,
будем искать
![]() в виде
в виде
![]() .
Тогда
.
Тогда
![]() .
Подставляя
.
Подставляя
![]() и
и
![]() в исходное уравнение, получаем
в исходное уравнение, получаем
 .
.
Полученное для
![]() уравнение является уравнением с
разделяющимися переменными. Найдем его
решение:
уравнение является уравнением с
разделяющимися переменными. Найдем его
решение:
 ,
,
 ,
,
 ,
,
 .
Определим произвольную постоянную С.
Так как при
.
Определим произвольную постоянную С.
Так как при
![]() имеем
имеем
![]() ,
а
,
а
 ,
то
,
то
 при
при
![]() .
Тогда
.
Тогда
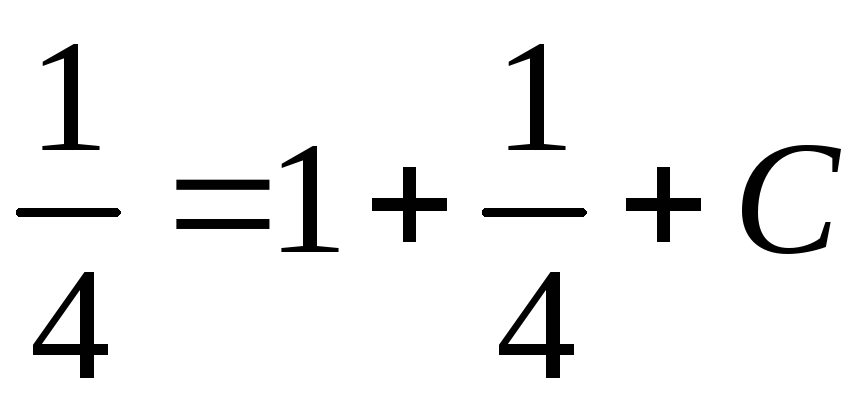 ,
С=
,
С=![]() .
Следовательно,
.
Следовательно,
 или
или
 . Знак плюс при извлечении корня выбран
потому, что
. Знак плюс при извлечении корня выбран
потому, что
 - положительное число. Неизвестную
функцию
- положительное число. Неизвестную
функцию
![]() определяем из уравнения
определяем из уравнения
 .
Найдем его решение:
.
Найдем его решение:
 ,
,
 ,
,
 ,
,
 .
Так как
.
Так как
![]() ,
то
,
то
![]() ,
,
![]() .
Следовательно,
.
Следовательно,
![]() ,
,
![]() .
.
Ответ:
![]() .
.
Задача 32.
Найти решение дифференциального
уравнения
 ,
удовлетворяющее начальным условиям
,
удовлетворяющее начальным условиям
![]() .
.
Найдем решение
однородного уравнения. Составляем
характеристическое уравнение:
![]() .
Найдем его корни:
.
Найдем его корни:
![]() .
.![]() Однородное
уравнение имеет два линейно независимых
решения
Однородное
уравнение имеет два линейно независимых
решения
![]() и
и
![]() .
Частное решение
.
Частное решение
![]() ищем в виде
ищем в виде
![]() ,
где функции
,
где функции
![]() и
и
![]() удовлетворяют системе уравнений:
удовлетворяют системе уравнений:
![]()
![]()
 .
.
Решая систему,
получаем:
 ,
,
 .
.
Находим
![]() и
и
![]() :
:
 ,
,
 .
Для вычисления первого интеграла сделаем
замену переменной
.
Для вычисления первого интеграла сделаем
замену переменной
![]() .
Тогда
.
Тогда
![]() ,
,
 .
Подставляя в выражение для интеграла,
получаем
.
Подставляя в выражение для интеграла,
получаем

![]()
При вычислении второго интеграла сделаем аналогичную замену переменных.

 .
.
Тогда

Общее решение
однородного уравнения равно:
![]() .
Общее
решение исходного уравнения запишется
в виде:
.
Общее
решение исходного уравнения запишется
в виде:

![]()
Из условия
![]() получаем
получаем
 .
.
Найдем производную
общего решения:

+
Из условия
![]() получаем:
получаем:
 .
.
Для определения
![]() и
и
![]() имеем систему уравнений
имеем систему уравнений

Решая эту систему, получаем
![]() ,
, .
.
 +
+
+![]()
 =
= +
+ =
=
 .
.
Ответ:
![]()

 .
.
Задача 33.
Найти общее решение дифференциального
уравнения
![]() .
.
Вначале найдем
общее решение соответствующего
однородного уравнения
![]() .
Составляем характеристическое уравнение
.
Составляем характеристическое уравнение
![]() .
Найдем его корни:
.
Найдем его корни:
![]() ;
;
![]() ;
;
![]() .
.
Общее решение
однородного уравнения запишется в виде:
![]() .
.
Исходное уравнение
имеет правую часть первого типа:
![]() ,
,
![]() ,
,
![]() .
Число
.
Число
![]() не встречается среди корней
характеристического уравнения, значит
кратность s=0.
Будем искать
не встречается среди корней
характеристического уравнения, значит
кратность s=0.
Будем искать
![]() в виде
в виде
![]() =
=![]() ,
где
,
где
![]() - многочлен второй степени. Тогда
- многочлен второй степени. Тогда
![]() =
=![]() .
Коэффициенты А , В и С определим из
условия, чтобы частное решение
удовлетворяло исходному уравнению.
Найдем
.
Коэффициенты А , В и С определим из
условия, чтобы частное решение
удовлетворяло исходному уравнению.
Найдем
 :
:
 ;
;
 .
.
Подставляя
 в исходное уравнение, получаем:
в исходное уравнение, получаем:
![]()
Приводим подобные в левой части уравнения:
![]() .
.
Приравнивая коэффициенты при одинаковых степенях х в правой и левой частях, получаем:
![]()
![]()
![]()
Следовательно
А=1, В=0, С=3. Тогда частное решение запишется
в виде
![]() =
=![]() .
.
Следовательно, общее решение исходного уравнения равно:
![]()
![]() +
+![]() .
.
Ответ:
![]()
![]() +
+![]() .
.
Задача 34.
Найти решение дифференциального
уравнения
![]() ,
удовлетворяющее начальным условиям
,
удовлетворяющее начальным условиям
![]() .
.
Вначале найдем
общее решение соответствующего
однородного уравнения. Составляем
характеристическое уравнение:
![]() .
Найдем его корни:
.
Найдем его корни:
![]() ;
;
![]() ;
;
![]() .
.
Общее решение
однородного уравнения запишется в виде:
![]() .
.
Найдем частное
решение. Правую часть представим как
сумму двух функций
![]() и
и
![]() ,
где
,
где
![]() =
=![]() ,
,
![]() .
.
Рассмотрим уравнение
![]()
![]() .
.
Функция
![]() =
=![]() соответствует правой части первого
типа:
соответствует правой части первого
типа:
![]() ,
,
![]() ,
n=1.
Число =1
не встречается среди корней
характеристического уравнения, значит
кратность s=0.
Будем искать
,
n=1.
Число =1
не встречается среди корней
характеристического уравнения, значит
кратность s=0.
Будем искать
![]() в виде
в виде
![]() =
=![]() ,
где
,
где
![]() - многочлен первой степени. Тогда
- многочлен первой степени. Тогда
![]() =
=![]() .
Коэффициенты А и В определим из условия,
чтобы частное решение удовлетворяло
исходному уравнению. Найдем
.
Коэффициенты А и В определим из условия,
чтобы частное решение удовлетворяло
исходному уравнению. Найдем
 :
:
 ;
;
 .
.
Подставляя
 в исходное уравнение, получаем:
в исходное уравнение, получаем:
![]()
=![]()
Сокращаем правую
и левую части на
![]() и
приводим подобные в левой части:
и
приводим подобные в левой части:
![]() .
.
Приравнивая
коэффициенты при одинаковых степенях
![]() в правой и левой частях, получаем:
в правой и левой частях, получаем:
![]() .
Следовательно А=1, В=0. Тогда частное
решение запишется в виде
.
Следовательно А=1, В=0. Тогда частное
решение запишется в виде
![]() =
=![]() .
.
Рассмотрим уравнение
![]() .
.
Функция
![]() =
=![]() соответствует правой части первого
типа:
соответствует правой части первого
типа:
![]() ,
,
![]() ,
n=0.
Число =2
один раз встречается среди корней
характеристического уравнения, значит
кратность s=1.
Будем искать
,
n=0.
Число =2
один раз встречается среди корней
характеристического уравнения, значит
кратность s=1.
Будем искать
![]() в виде
в виде
![]() =
=![]() ,
где
,
где
![]() - многочлен первой степени. Тогда
- многочлен первой степени. Тогда
![]() =
=![]() .
Коэффициенты А и В определим из условия,
чтобы частное решение удовлетворяло
исходному уравнению. Найдем
.
Коэффициенты А и В определим из условия,
чтобы частное решение удовлетворяло
исходному уравнению. Найдем
 :
:
 ;
;
 .
.
Подставляя
 в исходное уравнение, получаем:
в исходное уравнение, получаем:
![]()
![]()
Сокращаем правую
и левую части на
![]() и
приводим подобные в левой части:
и
приводим подобные в левой части:
![]() .
.
Следовательно
А=1. Тогда частное решение запишется в
виде
![]() =
=![]() .
.
