
3ДУ
.doc
2. Уравнения высших порядков
Далее перейдем к уравнениям более высокого порядка.
Дифференциальным
уравнением порядка
![]() ,
разрешенным относительно старшей
производной, называется дифференциальное
уравнение вида
,
разрешенным относительно старшей
производной, называется дифференциальное
уравнение вида
![]() .
.
Частным решением
дифференциального уравнения называется
любая функция
![]() ,
при подстановке которой в дифференциальное
уравнение, оно превращается в тождество.
,
при подстановке которой в дифференциальное
уравнение, оно превращается в тождество.
Задачей Коши для
дифференциального уравнения порядка
![]() называется задача отыскания решения
дифференциального уравнения
называется задача отыскания решения
дифференциального уравнения
![]() ,
,
удовлетворяющего условиям
![]() ,
,
![]() ,
,
![]() ,…,
,…,
![]() при
при
![]() .
.
Доказано, что при определенных условиях задача Коши имеет решение и при том единственное.
Общим решением
дифференциального уравнения
![]() называется совокупность функций
называется совокупность функций
![]() ,
где
,
где
![]() - произвольные постоянные, удовлетворяющая
условиям:
- произвольные постоянные, удовлетворяющая
условиям:
1. При любом наборе
произвольных постоянных
![]() функция
функция
![]() является частным решением дифференциального
уравнения;
является частным решением дифференциального
уравнения;
2. Для любых начальных
условий задачи Коши
![]() ,
,
![]() ,
,
![]() ,…,
,…,
![]() при
при
![]() существует
такой набор значений произвольных
постоянных
существует
такой набор значений произвольных
постоянных
![]() ,
что выполнены условия
,
что выполнены условия
![]() ,
,
![]() ,…….,
,…….,
![]()
5.Уравнения, допускающие понижение порядка.
Пусть дано уравнение порядка n вида
![]() ,
,
то есть в данное
уравнение явно не входят неизвестная
функция и производные этой функции до
порядка k-1
включительно. Введем новую неизвестную
функцию
![]() .
Производные функции
.
Производные функции
![]() выразятся через производные функции
выразятся через производные функции
![]() следующим образом:
следующим образом:
![]() ,…,
,…,
![]() .
Подставляя в исходное уравнение, получаем
.
Подставляя в исходное уравнение, получаем
![]() .
Полученное уравнение для функции
.
Полученное уравнение для функции
![]() является уравнением более низкого
порядка. Если функция
является уравнением более низкого
порядка. Если функция
![]() определена, то функция
определена, то функция
![]() определяется интегрированием соотношения
определяется интегрированием соотношения
![]() =
=![]() .
.
Задача 14. При x>0 найти общее решение дифференциального уравнения
![]() .
.
Это уравнение
явно не содержит y
и
![]() .
Обозначим
.
Обозначим
![]() .
Тогда:
.
Тогда:
![]() ,
,
![]() .
Подставляя в исходное уравнение, получаем
.
Подставляя в исходное уравнение, получаем
![]() .
.
Уравнение для
определения функции
![]() является уравнением с разделяющимися
переменными. Найдем его решение:
является уравнением с разделяющимися
переменными. Найдем его решение:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Так как
![]() ,
то
,
то
![]() =
=![]() .
Тогда
.
Тогда
![]() .
.
Обозначим
![]() .
.
Ответ:
![]() ,
где
,
где
![]() - произвольные постоянные.
- произвольные постоянные.
Задача 15. Найти общее решение дифференциального уравнения
![]() .
.
Данное уравнение
не содержит явно неизвестную функцию
![]() .
Введем новую неизвестную функцию
.
Введем новую неизвестную функцию
![]() .
Тогда
.
Тогда
![]() и уравнение преобразуется к виду
и уравнение преобразуется к виду
![]() .
.
Полученное уравнение
является линейным дифференциальным
уравнением первого порядка. Будем искать
![]() в виде
в виде
![]() .
Тогда
.
Тогда
![]()
![]() .
Подставляя
.
Подставляя
![]() и
и
![]() в исходное уравнение, получаем:
в исходное уравнение, получаем:
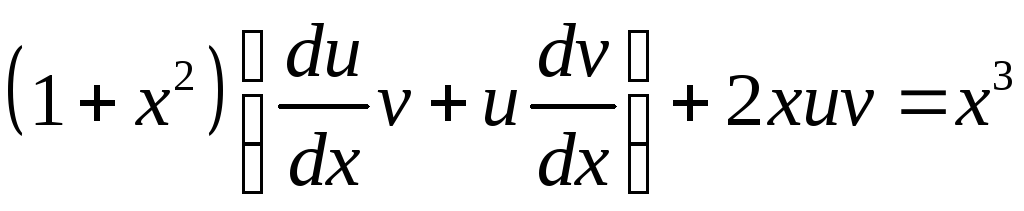 ;
;
 .
.
Выберем функцию
![]() из условия
из условия
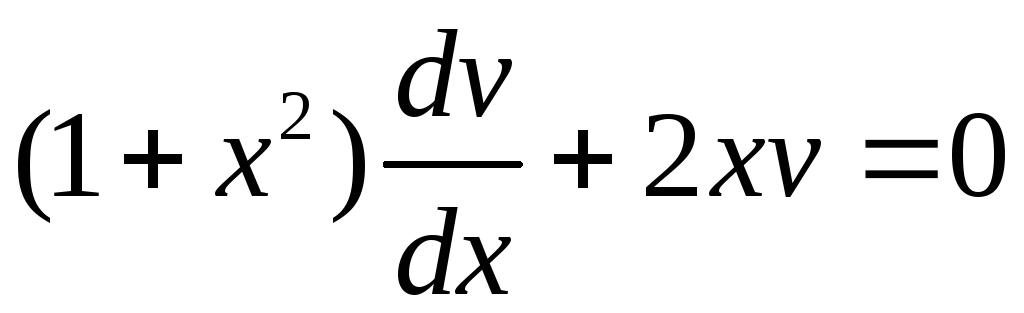 .
Уравнение для функции
.
Уравнение для функции
![]() является уравнением с разделяющимися
переменными. Найдем его решение:
является уравнением с разделяющимися
переменными. Найдем его решение:
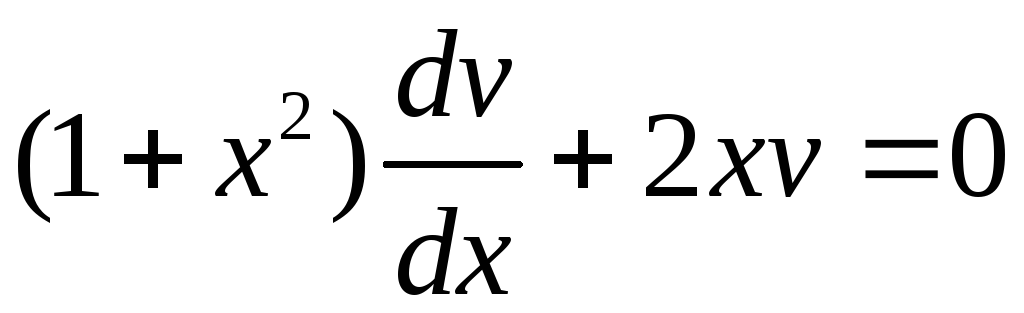 ,
,
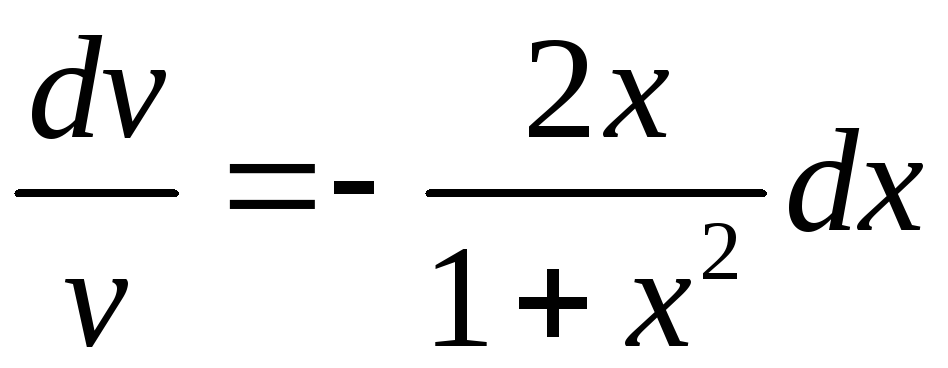 ;
;
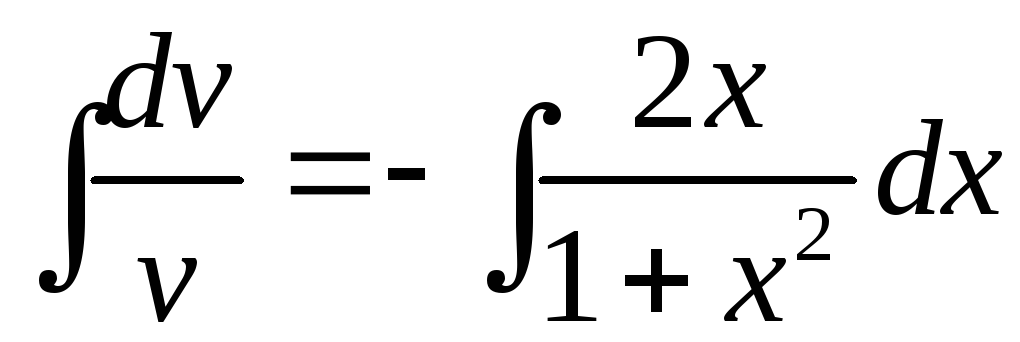 ;
;
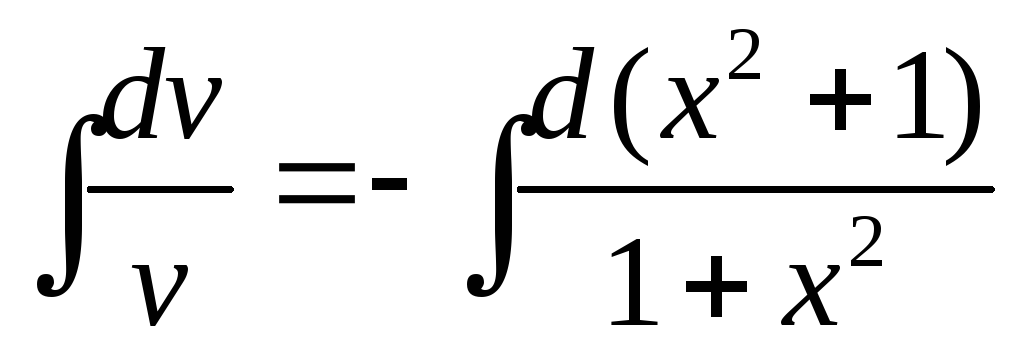 ;
;
![]() ,
,
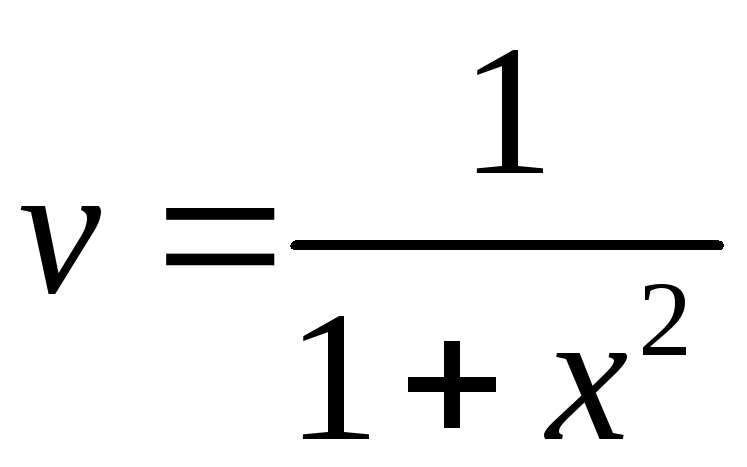 .
.
Найдем функцию
![]() :
:
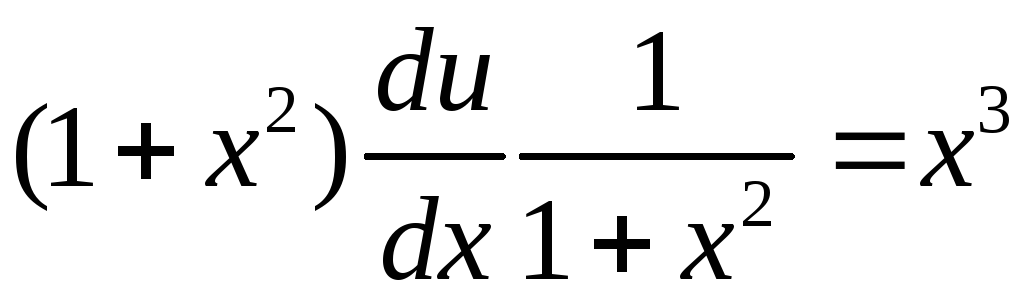 ;
;
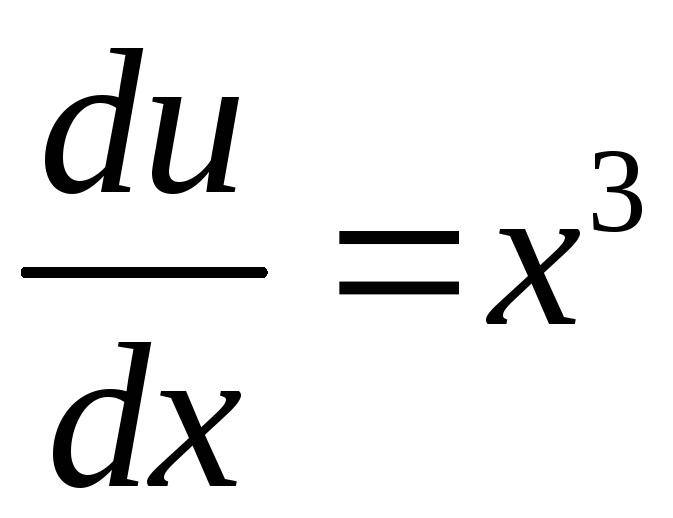 ;
;
 .
.
Тогда
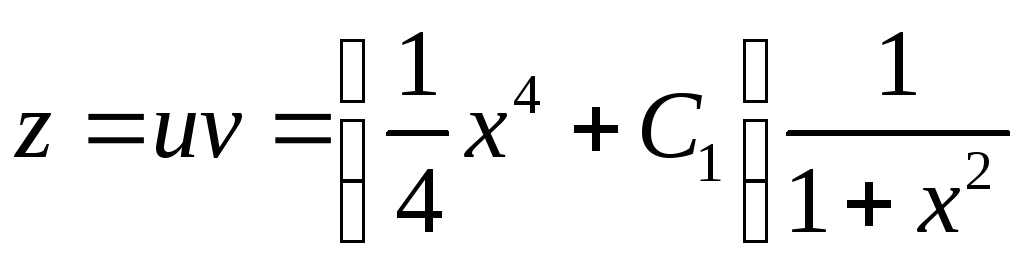 =
=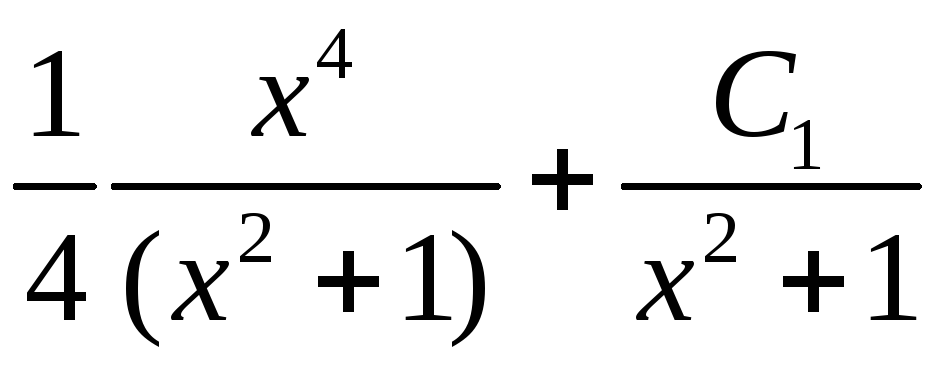 .
.
Определим
![]() .
.
![]()
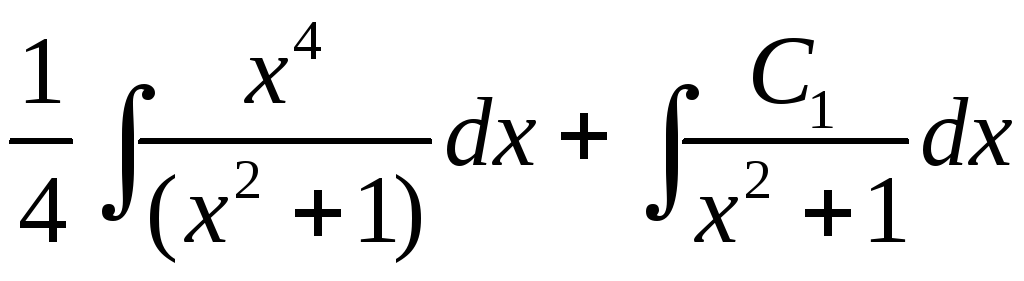 =
=
=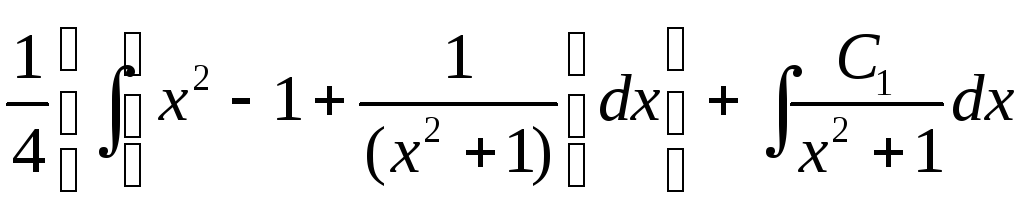 =
=
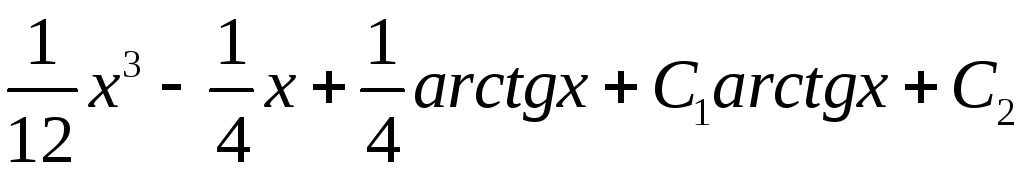 .
.
Так как
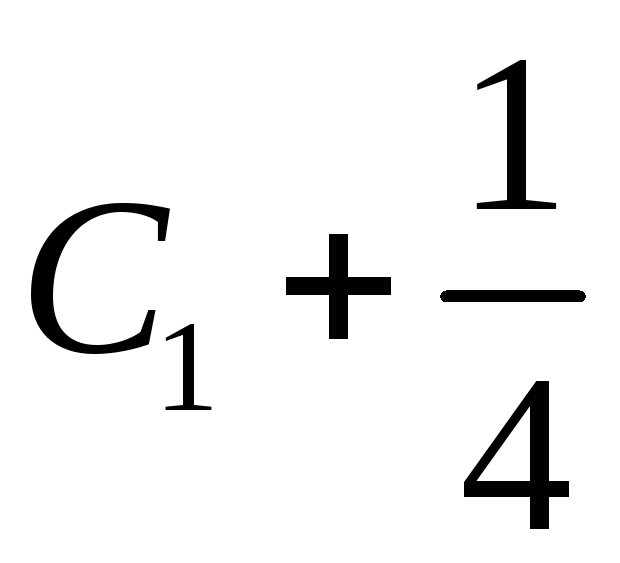 является так же произвольной постоянной,
то окончательный ответ может быть
записан в виде
является так же произвольной постоянной,
то окончательный ответ может быть
записан в виде
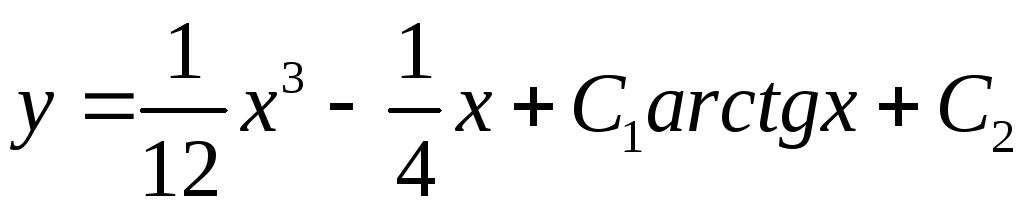 .
.
Ответ:
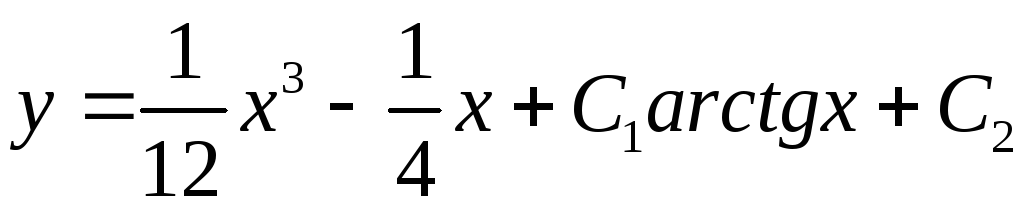 .
.
Второй тип
уравнений, допускающих понижение
порядка, - это уравнения, которые явно
не содержат независимую переменную
![]() .
(Мы будем рассматривать только уравнения
второго порядка, однако предложенный
метод применим и для уравнений более
высокого порядка.) Пусть дано уравнение
вида
.
(Мы будем рассматривать только уравнения
второго порядка, однако предложенный
метод применим и для уравнений более
высокого порядка.) Пусть дано уравнение
вида
![]() .
.
Будем искать
производную
![]() как
функцию
как
функцию
![]() в виде
в виде
![]() ,
где
,
где
![]() - неизвестная функция. Тогда
- неизвестная функция. Тогда
![]() =
=![]() =
=![]() =
=![]() .
.
Подставляя
![]() и
и
![]() в
исходное уравнение, получаем
в
исходное уравнение, получаем
![]() .
.
Полученное уравнение
является уравнением первого порядка
для функции
![]() .
Если нам удастся найти функцию
.
Если нам удастся найти функцию
![]() ,
то для определении
,
то для определении
![]() имеем уравнение
имеем уравнение
![]() ,
которое является уравнением с
разделяющимися пере6менными.
,
которое является уравнением с
разделяющимися пере6менными.
Замечание. При
изложенном методе могут быть потерянны
решения
![]() ,
то есть
,
то есть
![]() .
Поэтому такие решения рекомендуется
выписывать отдельно.
.
Поэтому такие решения рекомендуется
выписывать отдельно.
Задача 16. Найти решение задачи Коши:
![]() ,
,
![]() ,
,
![]() .
.
Будем искать
![]() в виде
в виде
![]() .
Тогда
.
Тогда
![]() .
Подставляя
.
Подставляя
![]() и
и
![]() в исходное уравнение, получаем
в исходное уравнение, получаем
![]() .
Полученное для
.
Полученное для
![]() уравнение является уравнением с
разделяющимися переменными. Найдем его
решение:
уравнение является уравнением с
разделяющимися переменными. Найдем его
решение:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Определим произвольную постоянную С.
Так как при
.
Определим произвольную постоянную С.
Так как при
![]() имеем
имеем
![]() ,
а
,
а
![]() ,
то
,
то
![]() при
при
![]() .
Тогда 32=32+С, С=0. Следовательно,
.
Тогда 32=32+С, С=0. Следовательно,
![]() или
. Знак плюс при извлечении корня выбран
потому, что
или
. Знак плюс при извлечении корня выбран
потому, что
![]() - положительное число. Неизвестную
функцию
- положительное число. Неизвестную
функцию
![]() определяем из уравнения
определяем из уравнения
![]() .
Найдем его решение:
.
Найдем его решение:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() ,
,
![]() .
Следовательно,
.
Следовательно,
![]() .
.
Ответ:
![]() .
.
Задача 17. Найти решение задачи Коши:
![]() ,
,
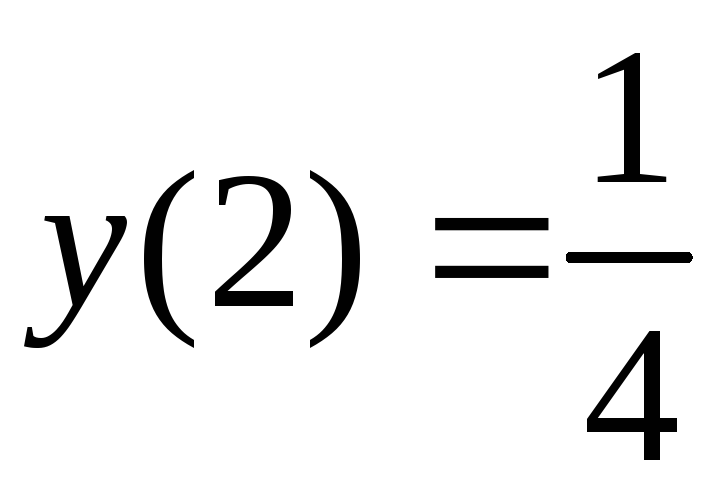 ,
,
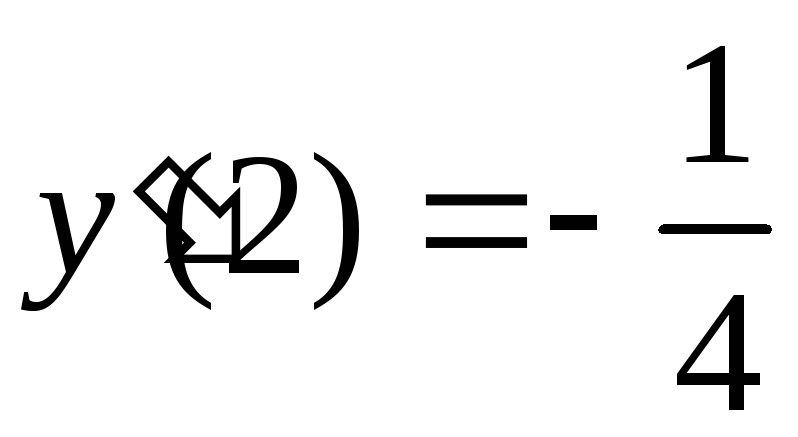 .
.
Будем искать
![]() в виде
в виде
![]() .
Тогда
.
Тогда
![]() .
Подставляя
.
Подставляя
![]() и
и
![]() в исходное уравнение, получаем
в исходное уравнение, получаем
![]() .
.
Полученное для
![]() уравнение является уравнением с
разделяющимися переменными. Найдем его
решение:
уравнение является уравнением с
разделяющимися переменными. Найдем его
решение:
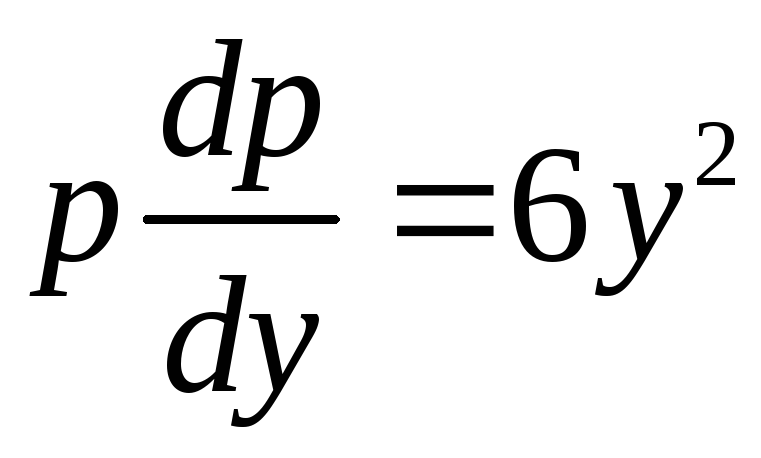 ,
,
![]() ,
,
![]() ,
,
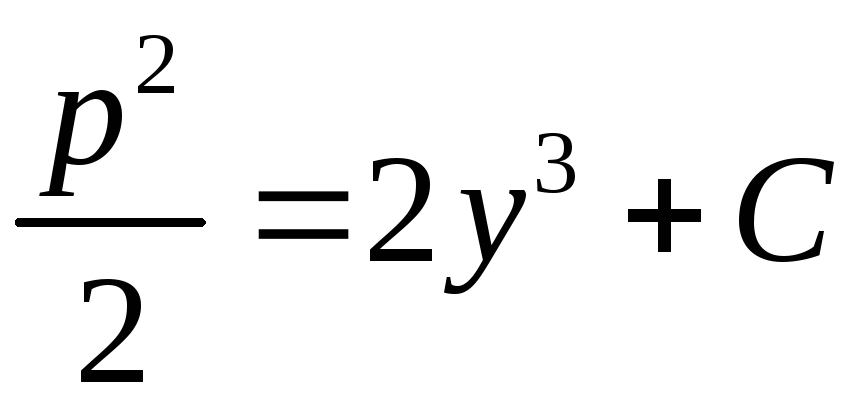 .
Определим произвольную постоянную С.
Так как при
.
Определим произвольную постоянную С.
Так как при
![]() имеем
имеем
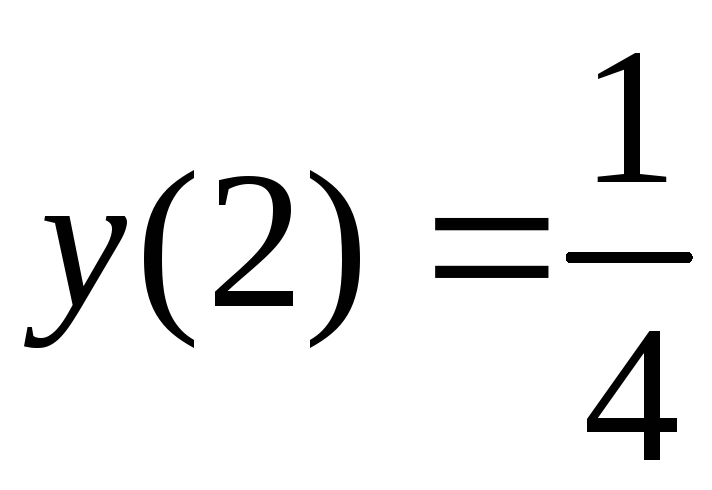 ,
а
,
а
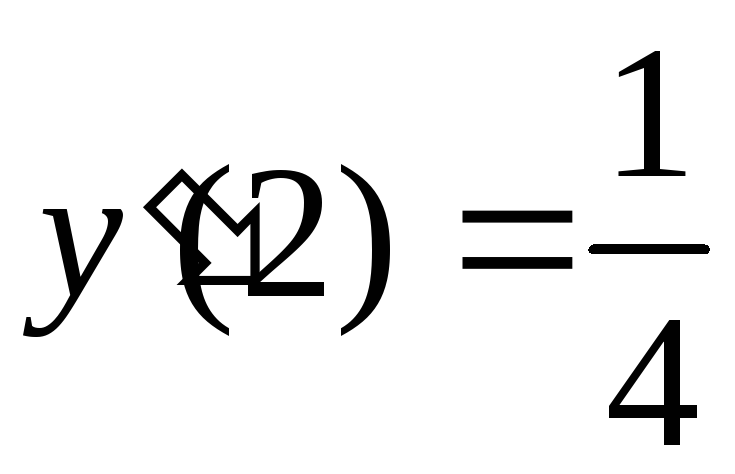 ,
то
,
то
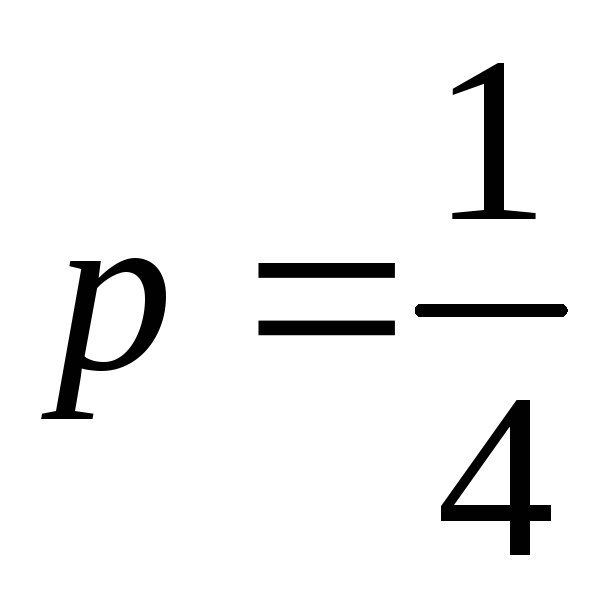 при
при
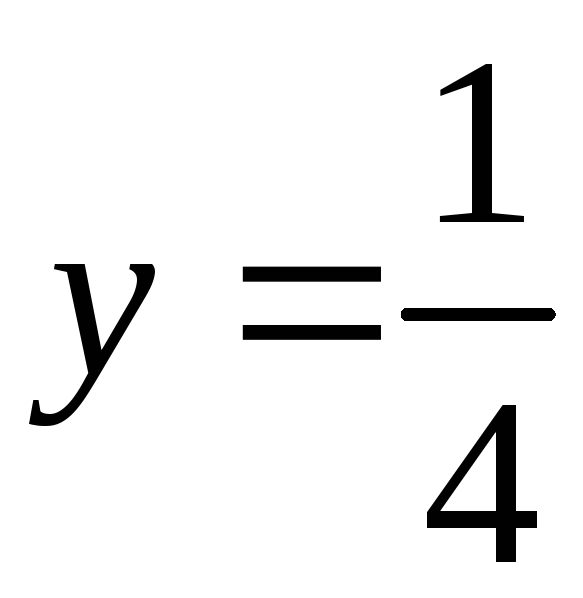 .
Тогда
.
Тогда
![]() =
=![]() +С,
С=0. Следовательно,
+С,
С=0. Следовательно,
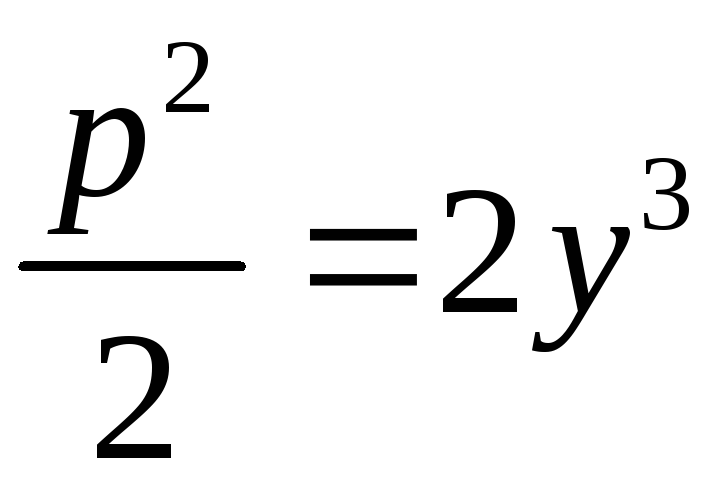 или
. Знак плюс при извлечении корня выберем
потому, что
или
. Знак плюс при извлечении корня выберем
потому, что
 - положительное число. Неизвестную
функцию
- положительное число. Неизвестную
функцию
![]() определяем из уравнения
определяем из уравнения
![]() .
Найдем его решение:
.
Найдем его решение:
 ,
,
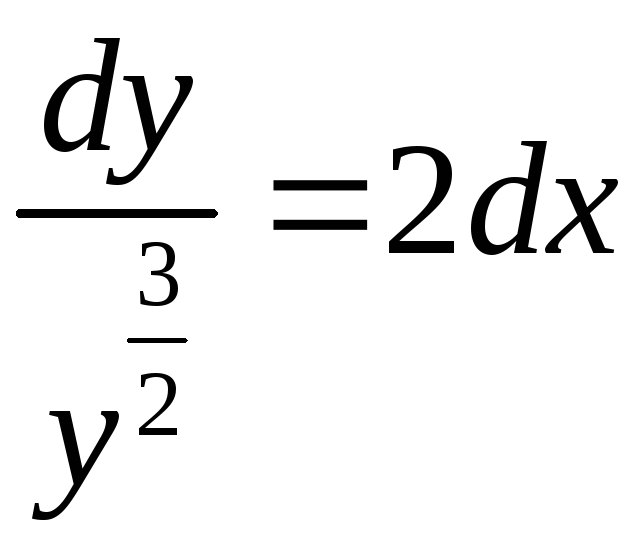 ,
,
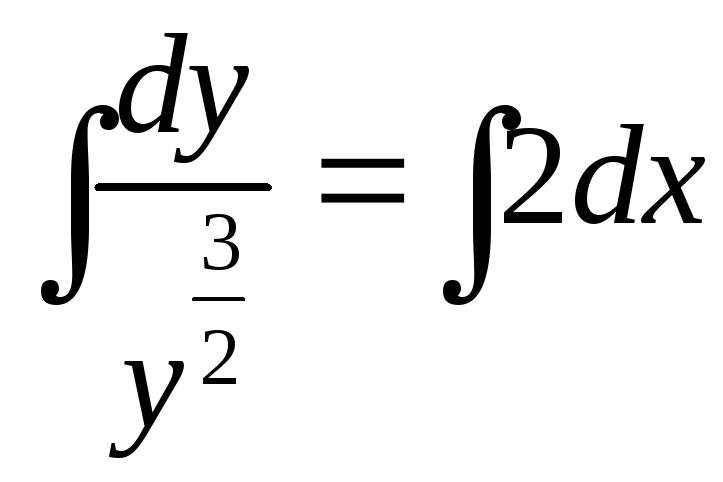 ,
,
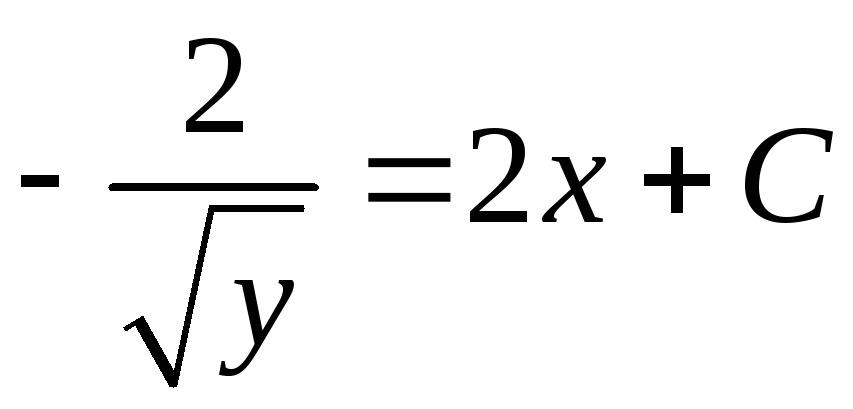 ,
,
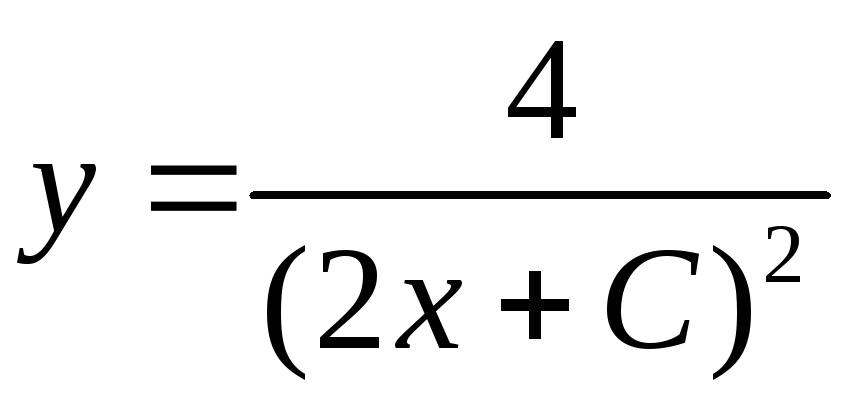 .
Так как
.
Так как
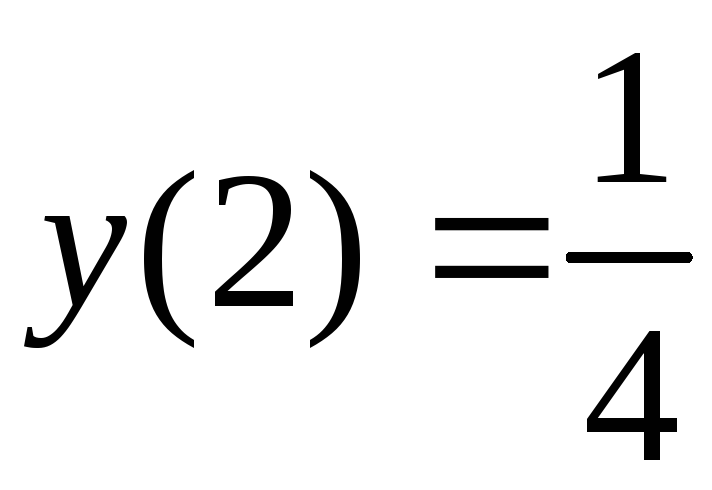 ,
то
,
то
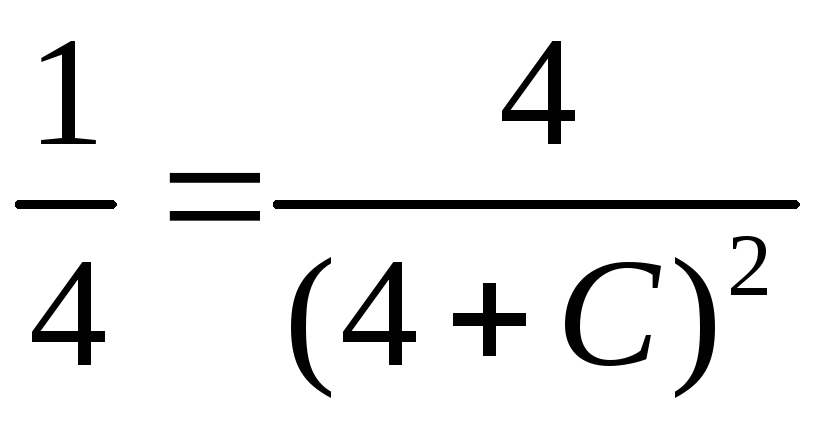 ,
,
![]() .
Следовательно,
.
Следовательно,
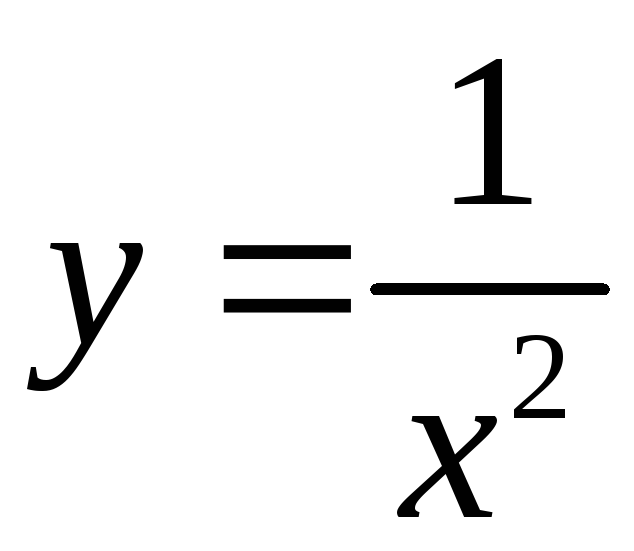 .
.
Ответ:
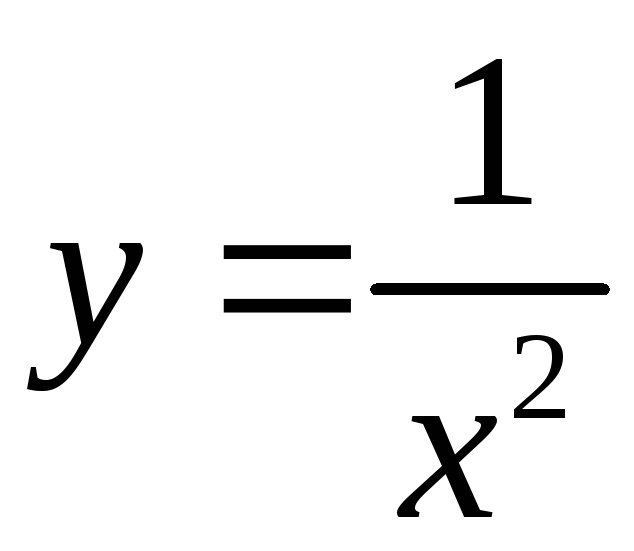 .
.
Задача 18. Решить задачу Коши
![]() ,
,
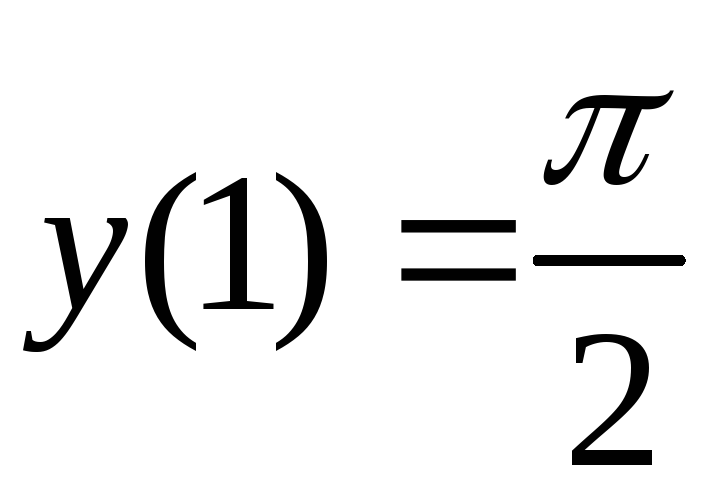 ,
,
![]() .
.
Будем искать
![]() в виде
в виде
![]() .
Тогда
.
Тогда
![]() .
Подставляя
.
Подставляя
![]() и
и
![]() в исходное уравнение, получаем
в исходное уравнение, получаем
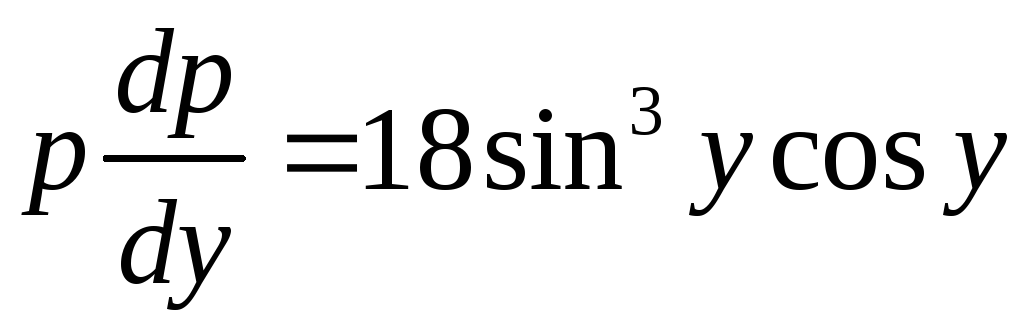 .
.
Полученное для
![]() уравнение является уравнением с
разделяющимися переменными. Найдем его
решение:
уравнение является уравнением с
разделяющимися переменными. Найдем его
решение:
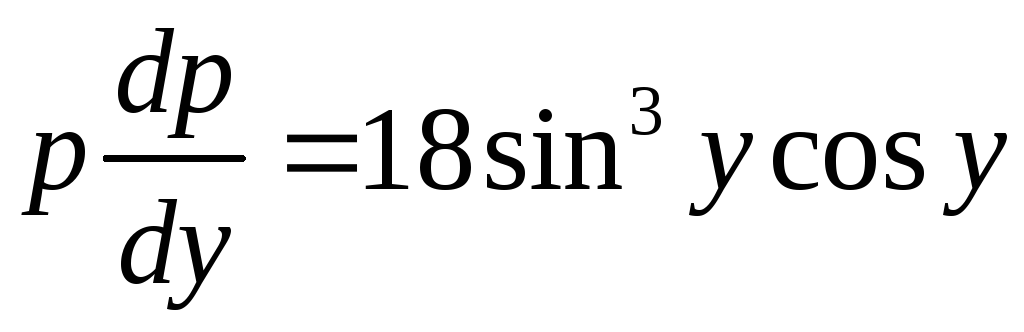 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
 .
Определим произвольную постоянную С.
Так как при
.
Определим произвольную постоянную С.
Так как при
![]() имеем
имеем
 ,
а
,
а
![]() ,
то
,
то
![]() при
при
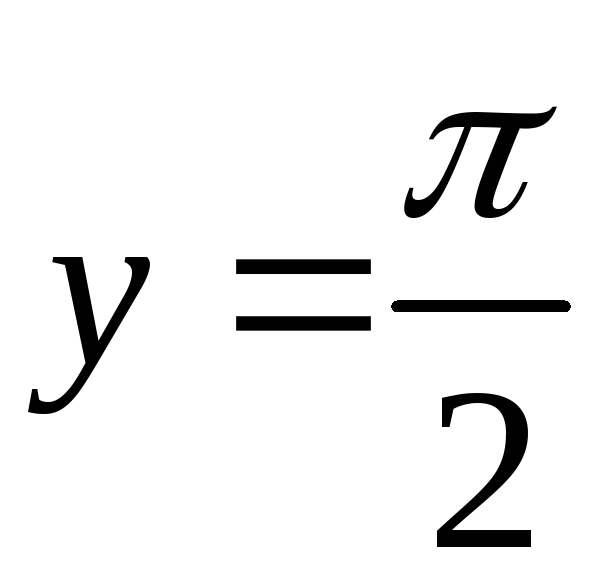 .
Тогда
.
Тогда
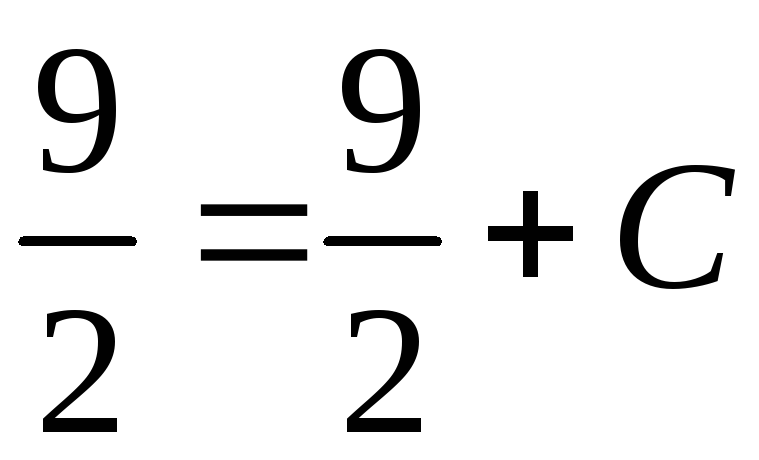 ,
С=0. Следовательно,
,
С=0. Следовательно,
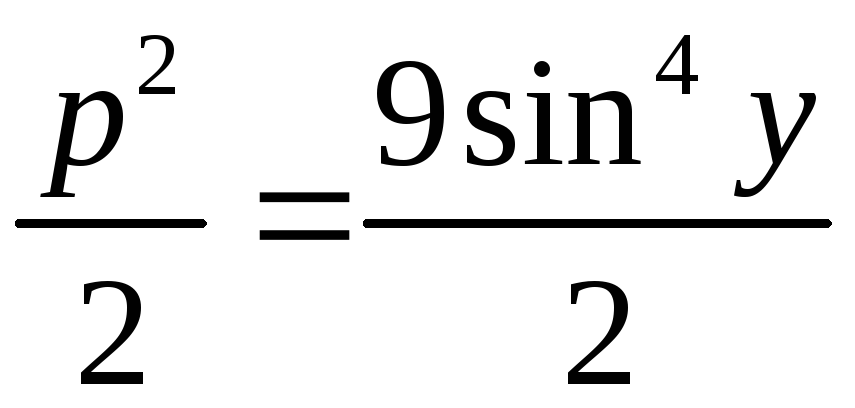 или
или
![]() .
Знак плюс при извлечении корня выберем
плюс потому, что
.
Знак плюс при извлечении корня выберем
плюс потому, что
![]() - положительное число. Тогда
- положительное число. Тогда
![]() .
Неизвестную функцию
.
Неизвестную функцию
![]() определяем из уравнения
определяем из уравнения
 .
Найдем его решение:
.
Найдем его решение:
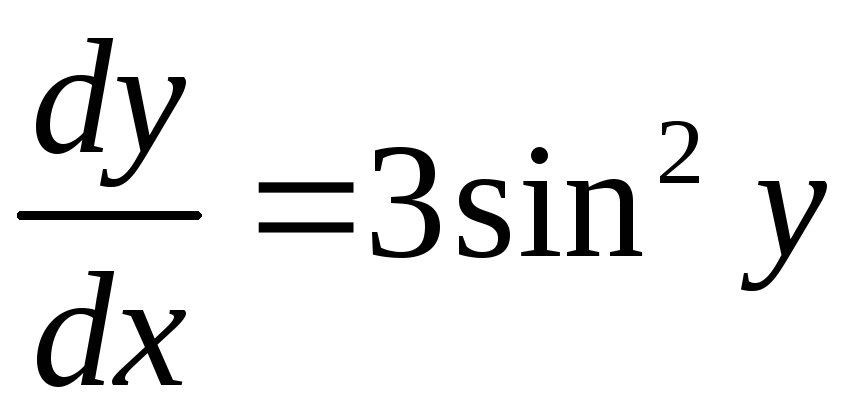 ,
,
 ,
,
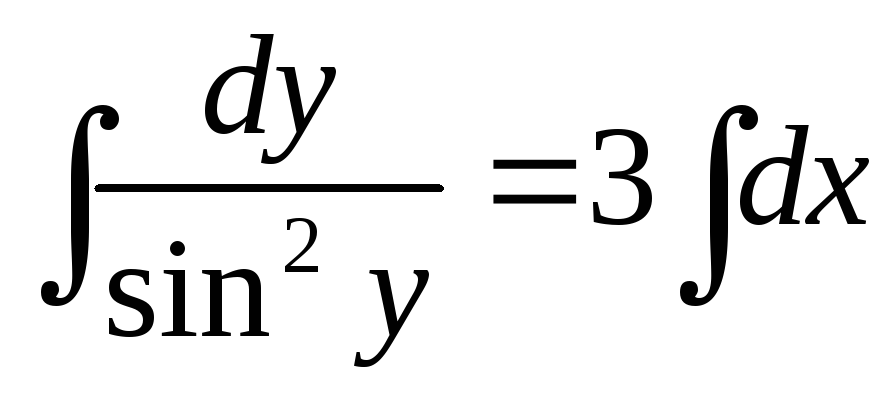 ,
,
![]() .
Так как
.
Так как
 ,
то
,
то
![]() ,
,
![]() .
.
Следовательно,
![]() .
.
Ответ:
![]() .
.
