
2ДУ
.doc
1.Дифференциальные уравнения первого порядка
Прежде чем перейти к решению конкретных типов задач, напомним некоторые общие положения, касающиеся дифференциальных уравнений первого порядка.
Дифференциальным уравнением первого порядка, разрешенным относительно производной, называется соотношение вида
 .
.
Частным решением
дифференциального уравнения называется
любая функция
![]() ,
при подстановке которой в дифференциальное
уравнение, оно превращается в тождество.
,
при подстановке которой в дифференциальное
уравнение, оно превращается в тождество.
Задачей Коши для дифференциального уравнения первого порядка называется задача отыскания решения дифференциального уравнения
 ,
,
удовлетворяющего
условиям,
![]() при
при
![]() .
.
Доказано, что если
в некоторой области функция
![]() непрерывна вместе со своей частной
производной
непрерывна вместе со своей частной
производной
![]() ,
то в этой области задача Коши имеет
решение и при том единственное.
,
то в этой области задача Коши имеет
решение и при том единственное.
Общим решением
дифференциального уравнения первого
порядка в некоторой области называется
совокупность функций
![]() (С – произвольная постоянная),
удовлетворяющая двум условиям:
(С – произвольная постоянная),
удовлетворяющая двум условиям:
1.При любом значении
произвольной постоянной С функция
![]() является частным решением дифференциального
уравнения;
является частным решением дифференциального
уравнения;
2. Для любых начальных
условий задачи Коши
![]() при
при
![]() найдется такое значение произвольной
постоянной
найдется такое значение произвольной
постоянной
![]() такое что
такое что
![]() .
.
Если общее решение
![]() неявно определятся соотношением вида
неявно определятся соотношением вида
![]() ,
то такое соотношение называется общим
интегралом дифференциального уравнения
первого порядка.
,
то такое соотношение называется общим
интегралом дифференциального уравнения
первого порядка.
Теперь перейдем к конкретным типам дифференциальных уравнений первого порядка
1.Уравнения с разделяющимися переменными.
Определение. Уравнением с разделяющимися переменными называется уравнение, которое может быть записано в виде:
![]() .
.
Можно предложить следующую схему решения этого уравнения. Разделяем переменные, то есть уравнение переписываем в виде:
![]() .
.
Интегрируя левую и правую части этого уравнения, получаем:
![]() ,
,
где С – произвольная постоянная.
Полученное соотношение является общим интегралом исходного дифференциального уравнения.
Замечание. Если
функция
![]() равна нулю в точках
равна нулю в точках
![]() ,
то функции
,
то функции
![]() ,
,
![]() ,….,
,….,
![]() являются решениями исходного уравнения.
При изложенном методе такие решения
могут быть потеряны, поэтому их
рекомендуется выписать отдельно.
являются решениями исходного уравнения.
При изложенном методе такие решения
могут быть потеряны, поэтому их
рекомендуется выписать отдельно.
Задача
1. Найти
общий интеграл дифференциального
уравнения. (Ответ представить в виде
![]() (x,y)=C).
(x,y)=C).
![]() .
.
Для того, что бы
убедиться, что данное уравнение
действительно является уравнением с
разделяющимися переменными, выразим
![]() .
Имеем
.
Имеем

Тогда
![]() ,
,
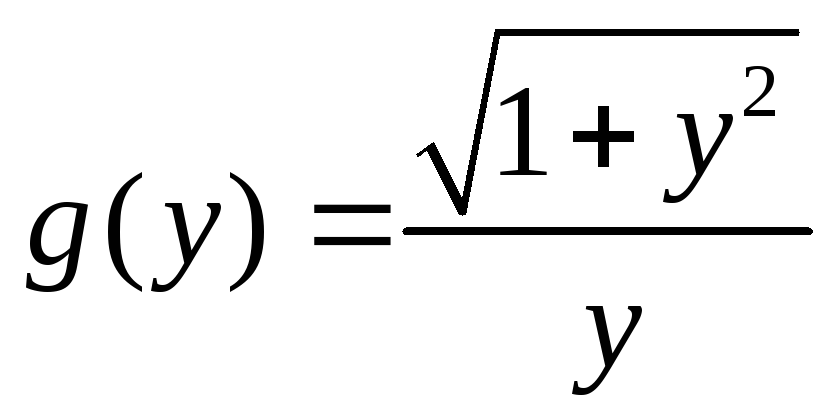 .
Заметим, что
.
Заметим, что
![]() .
Разделяем переменные:
.
Разделяем переменные:
![]() .
.
Интегрируя правую и левую части, получаем
![]() .
.
Приведем схему
вычисления интеграла:
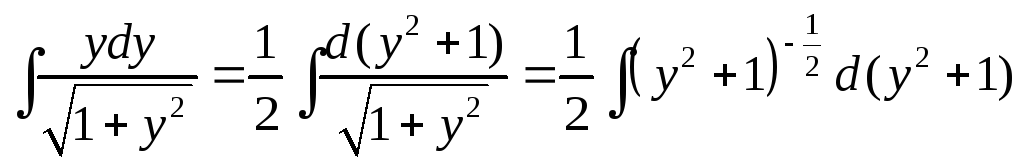 =
= .
.
После вычисления
интегралов имеем:
![]() .
.
Ответ:
![]() .
.
Задача 2. Найти общий интеграл дифференциального уравнения.
![]() .
.
Уравнение запишем в виде
 .
.
Тогда
 ,
,
![]() .
Заметим, что
.
Заметим, что
![]() при
при
![]() .
Следовательно, функция
.
Следовательно, функция
![]() является решением данного дифференциального
уравнения.
является решением данного дифференциального
уравнения.
В случае
![]() разделяем переменные:
разделяем переменные:
 .
.
Интегрируя правую и левую части, получаем
 .
.
Приведем схему вычисления интеграла
![]()
После вычисления
интегралов имеем:
![]() .
.
Потенцируя данное
выражение, получаем
![]() .
Отметим, что решение
.
Отметим, что решение
![]() содержится в полученном выражении
общего решения при С=0.
содержится в полученном выражении
общего решения при С=0.
Ответ:
![]() .
.
Задача 3. Найти общий интеграл дифференциального уравнения
![]() .
.
Тогда
![]() ,
,
![]() .
Заметим, что
.
Заметим, что
![]() .
Разделяем переменные:
.
Разделяем переменные:
![]() .
.
Интегрируя правую и левую части, получаем
![]() .
.
После вычисления
интегралов имеем:
![]() .
.
Ответ:
![]() .
.
Задача 4. Найти общий интеграл дифференциального уравнения
![]() .
.
Поясним, что такая
запись подразумевает под
![]() дифференциал независимой переменной,
под
дифференциал независимой переменной,
под
![]() - дифференциал неизвестной функции
(
- дифференциал неизвестной функции
(![]() =
=![]() ).
).
Перенесем
выражения, содержащие
![]() в левую часть уравнения, выражения,
содержащие -
в левую часть уравнения, выражения,
содержащие -
![]() в правую часть. После некоторых простых
преобразований, получаем
в правую часть. После некоторых простых
преобразований, получаем
![]() .
.
Разделяем переменные
 .
.
Интегрируя правую
и левую части, получаем  .
.
Приведем схему вычисления интеграла
 .
.
После вычисления интегралов имеем
 .
.
Потенцируя
полученное выражение, имеем
![]() .
.
Ответ:
![]() .
.
2. Однородные уравнения.
Определение. Однородным уравнением называется дифференциальное уравнение первого порядка, которое может быть записано в виде:
![]() .
.
Можно предложить
следующий метод его решения. Неизвестную
функцию
![]() будем искать в виде
будем искать в виде
![]() ,
где
,
где
![]() - неизвестная функция. Тогда
- неизвестная функция. Тогда
![]() .
Подставляя
.
Подставляя
![]() и
и
![]() в
исходное уравнение, получаем:
в
исходное уравнение, получаем:
![]() .
.
Данное уравнение представим в виде
![]() .
.
Полученное
уравнение является уравнением с
разделяющимися переменными для функции
![]() .
Метод его решения рассмотрен ранее.
.
Метод его решения рассмотрен ранее.
Задача 5. Найти общий интеграл дифференциального уравнения
![]() .
.
Данное уравнение
является однородным. Будем искать
неизвестную функцию
![]() в виде
в виде
![]() .
Тогда
.
Тогда
![]() .
Подставляя
.
Подставляя
![]() и
и
![]() в
исходное уравнение, получаем:
в
исходное уравнение, получаем:
![]() .
.
Полученное уравнение преобразуем к виду
![]() .
.
Разделяем переменные
![]() .
.
Интегрируем правую и левую части
![]() +
+![]() .
.
(В нашем случае
произвольную постоянную удобнее
обозначит не С, а
![]() ,
где
,
где
![]() .
Вычисляя интегралы в правой и левой
частях уравнения, получаем
.
Вычисляя интегралы в правой и левой
частях уравнения, получаем
![]() .
.
Потенцируя, имеем
![]() .
.
Избавляясь от знака модуля, получаем
![]() .
.
Поскольку
![]() ,
то полученное соотношение может быть
представлено в виде
,
то полученное соотношение может быть
представлено в виде
![]() .
.
Заметим, что в
уравнении
![]() ,
выражение
,
выражение
![]() при
при
![]() ,
,
![]() .
Следовательно, функции
.
Следовательно, функции
![]() и
и
![]() являются решениями дифференциального
уравнения для неизвестной функции
являются решениями дифференциального
уравнения для неизвестной функции
![]() ,
а значит, функции
,
а значит, функции
![]() и
и
![]() являются решениями исходного
дифференциального уравнения.
являются решениями исходного
дифференциального уравнения.
Решение
![]() содержится
в решении
содержится
в решении
![]() ,
если положить С=0.
,
если положить С=0.
Ответ:
![]() ,
,
![]() ,
где С – произвольная постоянная.
,
где С – произвольная постоянная.
Задача 6. Найти общий интеграл дифференциального уравнения.
![]() .
.
Поскольку данное
уравнение является однородным, то
неизвестную функцию
![]() будем искать в виде
будем искать в виде
![]() .
Тогда
.
Тогда
![]() .
Подставляя
.
Подставляя
![]() и
и
![]() в
исходное уравнение, получаем:
в
исходное уравнение, получаем:
![]() .
.
Полученное уравнение преобразуем к виду
![]()
Разделяем переменные
![]()
Интегрируем правую и левую части
![]() .
.
Вычисляя интегралы в правой и левой частях уравнения, получаем
![]() .
.
Поскольку
![]() ,
то полученное соотношение может быть
представлено в виде
,
то полученное соотношение может быть
представлено в виде
![]() .
.
Ответ:
![]() ,
где С – произвольная постоянная.
,
где С – произвольная постоянная.
Задача 7. Найти общий интеграл дифференциального уравнения
 .
.
Данное уравнение
является однородным. Будем искать
неизвестную функцию
![]() в виде
в виде
![]() .
Тогда
.
Тогда
![]() .
Подставляя
.
Подставляя
![]() и
и
![]() в исходное уравнение, получаем:
в исходное уравнение, получаем:
 .
.
Данное уравнение преобразуем к виду
 .
.
Поскольку правая
часть не равна нулю ни при каких значениях
![]() ,
то, разделяя переменные, получаем
,
то, разделяя переменные, получаем
 .
.
Интегрируя, имеем
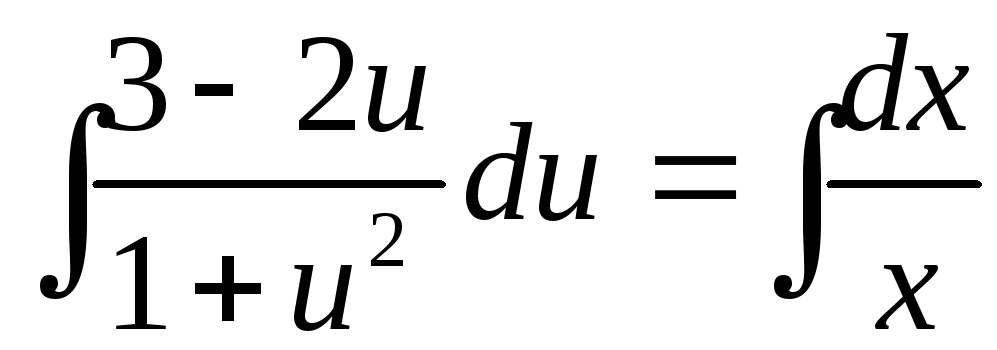 +С.
+С.
Приведем схему вычисления интеграла

![]() .
.
После вычисления интегралов получаем
![]() .
.
Поскольку
 ,
то выражение записываем в виде
,
то выражение записываем в виде
 .
.
Ответ:
 .
.
3. Линейные дифференциальные уравнения первого порядка.
Определение. Линейным дифференциальным уравнением первого порядка называется уравнение, которое может быть записано в виде
![]() ,
,
где Р(х) и Q(х) – известные функции.
Можно предложить
следующий метод решения этого уравнения.
Неизвестную функцию y(x)
будем искать в виде
![]() ,
где
,
где
![]() неизвестная
функция, а
неизвестная
функция, а
![]() - некоторая функция, выбранная специальным
образом. (Способ выбора
- некоторая функция, выбранная специальным
образом. (Способ выбора
![]() будет описан позже). Производная
будет описан позже). Производная
![]() равна:
равна:
![]() =
=![]() .
Подставляя
.
Подставляя
![]() и
и
![]() в исходное уравнение, получаем
в исходное уравнение, получаем
![]() +
+![]() .
.
Полученное уравнение преобразуем к виду
![]() .
.
Подберем функцию
![]() так, чтобы было выполнено:
так, чтобы было выполнено:
![]() .
.
(Это уравнение для
определения функции
![]() является уравнением с разделяющимися
переменными и нас интересует не его
общее решение, а какое либо частное
решение не тождественно равное нулю).
Тогда для определения
является уравнением с разделяющимися
переменными и нас интересует не его
общее решение, а какое либо частное
решение не тождественно равное нулю).
Тогда для определения
![]() имеем уравнение
имеем уравнение
![]() .
Из этого уравнения при известной функции
.
Из этого уравнения при известной функции
![]() находим
находим
![]() :
:
![]() =
=![]() ,
,
где С – произвольная постоянная.
Тогда общее решение
![]() имеет вид:
имеет вид:
![]()
Задача 8. Найти решение задачи Коши:
![]() ,
,
![]() .
.
Вначале найдем
общее решение этого уравнения. Будем
искать
![]() в виде
в виде
![]() .
Тогда
.
Тогда
![]()
![]() =
=![]() .
Подставляя
.
Подставляя
![]() и
и
![]() в исходное уравнение, получаем:
в исходное уравнение, получаем:
![]() +
+![]() ;
;
![]() .
.
Выберем функцию
![]() из условия
из условия
![]() .
Уравнение для функции
.
Уравнение для функции
![]() является уравнением с разделяющимися
переменными. Найдем его решение:
является уравнением с разделяющимися
переменными. Найдем его решение:
![]() ,
,
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Найдем функцию
![]() :
:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Тогда общее решение исходного уравнения имеет вид
![]() .
.
Произвольную
постоянную С определим из условия
![]() :
:
![]() ;
;
![]() .
.
Ответ:
![]() .
.
Задача 9. Найти общее решение дифференциального уравнения
![]() .
.
Данное дифференциальное
уравнение является линейным дифференциальным
уравнением первого порядка. Будем искать
![]() в виде
в виде
![]() .
Тогда
.
Тогда
![]()
![]() =
=![]() .
Подставляя
.
Подставляя
![]() и
и
![]() в исходное уравнение, получаем:
в исходное уравнение, получаем:
![]()
![]() ;
;
![]() .
.
Выберем функцию
![]() из условия
из условия
![]() .
Уравнение для функции
.
Уравнение для функции
![]() является уравнением с разделяющимися
переменными. Найдем его решение:
является уравнением с разделяющимися
переменными. Найдем его решение:
![]() ,
,
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Найдем функцию
![]() :
:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Тогда общее решение исходного уравнения имеет вид
![]() .
.
Ответ:
![]()
Задача 10. Найти решение задачи Коши
 ,
,
 .
.
Данное дифференциальное
уравнение является линейным дифференциальным
уравнением первого порядка. Будем искать
![]() в виде
в виде
![]() .
Тогда
.
Тогда
![]()
![]() .
Подставляя
.
Подставляя
![]() и
и
![]() в исходное уравнение, получаем:
в исходное уравнение, получаем:
 ;
;
 .
.
Выберем функцию
![]() из условия
из условия
 .
Уравнение для функции
.
Уравнение для функции
![]() является уравнением с разделяющимися
переменными. Найдем его решение:
является уравнением с разделяющимися
переменными. Найдем его решение:
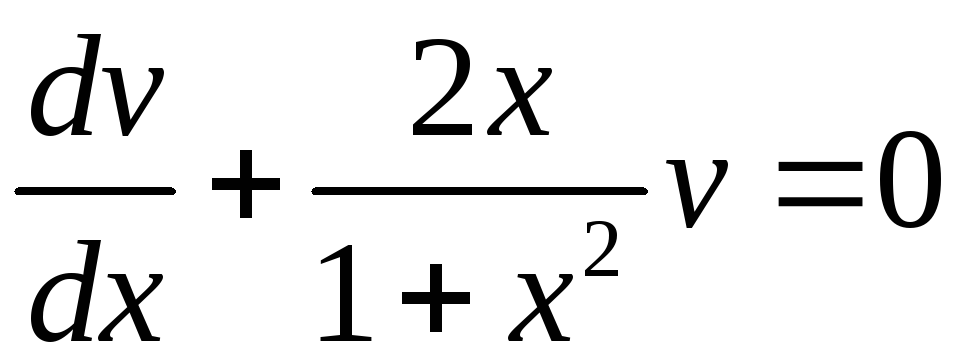 ,
,
 ;
;
 ;
;
 ;
;
![]() ,
,
 .
.
Найдем функцию
![]() :
:
 ;
;
 ;
;
 .
.
Тогда общее решение исходного уравнения имеет вид
 .
.
Определим произвольную постоянную С.
Так как
 ,
то имеем
,
то имеем
 ,
,

Ответ:

4. Уравнение Бернулли.
Определение. Уравнением Бернулли называется дифференциальное уравнение первого порядка, которое может быть записано в виде
![]() .
.
Можно предложить
следующий метод решения этого уравнения.
Неизвестную функцию y(x)
будем искать в виде
![]() ,
где
,
где
![]() -
неизвестная функция, а
-
неизвестная функция, а
![]() - некоторая функция, выбранная специальным
образом. (Способ выбора
- некоторая функция, выбранная специальным
образом. (Способ выбора
![]() будет описан позже). Производная
будет описан позже). Производная
![]() равна:
равна:
![]() =
=![]() .
Подставляя
.
Подставляя
![]() и
и
![]() в исходное уравнение, получаем
в исходное уравнение, получаем
![]() +
+![]() .
.
Полученное уравнение преобразуем к виду
![]() .
.
