IV. Контролируемая деталь как элемент разветвленной магнитной цепи

Магнитные цепи с последовательно-параллельным соединением нескольких элементов

Для обеспечения намагничивания, исключения пагубного влияния размагничивающего фактора коротких деталей проводят намагничивание одновременно нескольких последовательно составленных деталей.

Если в первом приближении можно не учитывать магнитные потоки рассеяния, ответвляющиеся в воздух от главной магнитной цепи, то расчет сложной магнитной цепи оказывается аналогичным расчету соответствующей сложной нелинейной электрической цепи.

В простейшем случае последовательного соединения всех участков магнитной цепи полная магнитодвижущая сила F = wi, определяемая током i в обмотке, имеющей w витков, равна сумме магнитодвижущих сил на отдельных учатках, т.е.:

_{Если можно пренебречь потоками рассеяния, то потоки Ф во всех последовательно соединенных участках, во всех сечениях sk данного участка будут одинаковы. Применяя закон магнитной цепи для всей магнитной цепи и для ее участков, будем иметь:}

_{RM – магнитное сопротивление всей магнитной цепи; RMk – магнитное сопротивление ее k-го участка, включая воздушные зазоры. Подставляя эти выражения в равенство F=∑Fk и сокращая на F, получаем:}

Если весь участок состоит из однородного материала, то:

где l_k — длина; μ_k — абсолютная магнитная проницаемость k-го участка, и соответственно:

Если известны значения индукции и материал, можно по кривым намагничивания найти для каждого участка значение напряженности поля H. Напряженность поля численно равна МДС, приходящейся на единицу длины. Поэтому МДС, необходимая для прохождения потока через данный участок цепи, равна произведению H_kl_k. В случае последовательного соединения большого числа элементов цепи полная искомая МДС, необходимая для образования заданного потока, равна сумме МДС:

wi = ∑H_kl_k = Н₁l₁ + Н₂l₂+ ...

Причем составляющая МДС, необходимая собственно для исследуемой детали, может быть существенно меньше общей МДС, определяемой зазорами, различными сечениями отдельных элементов магнитной цепи. Магнитный поток распределяется в отдельных местах неравномерно по сечению. Так, около краев детали происходит сгущение линий магнитной индукции. Соответственно эти места сильно насыщены и магнитная проницаемость их сравнительно невелика. Последнее обстоятельство учитывают соответствующими опытными коэффициентами.

Многие детали машин (см., например, рис. 54, а), могут быть представлены разветвленной магнитной цепью. Так как магнитные цепи нелинейны, то метод их расчета аналогичен методам расчета нелинейных электрических цепей. Пусть имеется деталь (рис 54, а), которую представим как разветвленную магнитную цепь, изображенную на рис. 54, б. При расчете необходимо использовать кривую намагничивания материала В = f(H), дающую зависимость магнитной индукции от напряжения магнитного поля (рис. 54, в).

Пользуясь кривой намагничивания, строим кривые Ф = f(F) для каждого участка в отдельности (кривые 1-3 на рис. 54, г). Для построения этих кривых необходимо умножить координаты кривой намагничивания, изображенной на рис. 54, в, на сечения участков и абсциссы - на длины участков. Например, кривую 1, дающую зависимость Ф₁ = f(F₁), получим умножением ординат кривой на рис. 54, в на s₁, и абсцисс на l₁. Так как

Ф₁ = Ф₂ + Ф₃ и F₂ = F₃ = F₂₃,

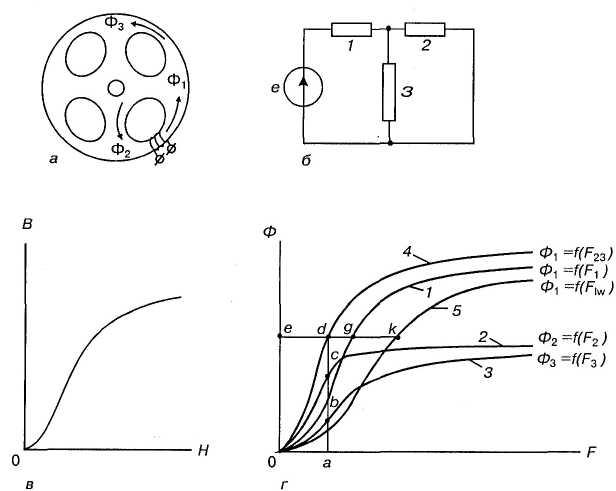
Рис. 54. К расчету намагничивания детали (а) со сложной геометрией; б — схема замещения; в — кривая намагничивания материала; г — кривые намагничивания отдельных частей одной и той же детали (а).то, складывая ординаты кривых 2 и 3 на рис. 54, г, определяющие зависимости , получим кривую 4, дающую зависимость . Например, точка d кривой 4 находится из суммы: ad = ab + ас.

Полная МДС iw равна сумме МДС F₁, и F₂₃, необходимых для проведения потока через первый участок и через параллельно соединенные второй и третий участки:

iw = F₁ + F₂₃.

Поэтому, складывая абсциссы кривых 1 и 4, определяющих зависимости Ф₁ = f(F₁) и Ф₁ = f(F₂₃) получаем кривую 5, дающую связь Ф₁ = f(iw). Например, точка k кривой 5 находится из суммы ek = ed + eg.

Видно, что метод расчета этой разветвленной магнитной цепи аналогичен методу расчета соответствующей, показанной на рис. 54, б электрической цепи. Учитывая потоки рассеяния, вносим поправки в значения магнитных потоков в различных сечениях каждого участка магнитной цепи. После этого требуется внести коррективы в значения потоков и МДС, чтобы удовлетворялись законы магнитной цепи. Новому распределению МДС будет соответствовать новая картина и новые значения потоков рассеяния. Продолжая действовать таким путем, можно приблизиться к истинной картине распределения потоков и МДС.

Расчет цепей с постоянными магнитами

Явление остаточного намагничивания, характерное для ферромагнитных веществ, широко используется при магнитопорошковой дефектоскопии. Намагничивающие устройства на основе мощных постоянных магнитов из редкоземельных металлов вытесняют электромагниты.

Расмотрим постоянный магнит с воздушным зазором (рис. 55, а).

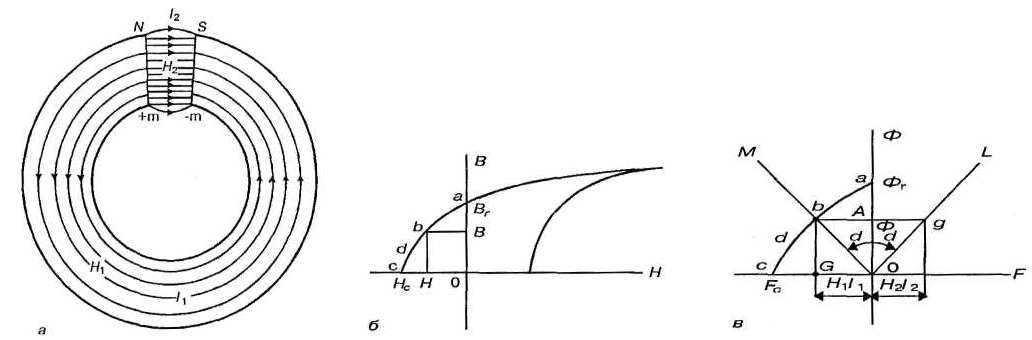
Рис. 55. К расчету цепи: а – цепь с постоянным магнитом; б – часть петли гистерезиса, снятой при большом насыщении; в – зависимость магнитного потока Ф от магнитодвижущей силы F.

Форма магнита не имеет принципиального значения. Будем обозначать все величины, относящиеся к зазору, индексом 2, и величины, относящиеся к телу магнита, индексом 1. Физически поле магнита создается элементарными токами в теле магнита. Однако напряженность поля Н, которой мы пользуемся при технических расчетах, определяется так, что равен только макроскопическим токам, протекающим в проводниках, охватываемых контуром интегрирования, и в его величину не входят элементарные токи в намагниченных телах. В случае постоянного магнита, так как макроскопических токов нет, имеем всюду . В частности, этот интеграл также равен нулю вдоль пути по оси магнита и зазора. Следовательно, имеем:

_т.е.

где l₁ и l₂ — длины осей магнита и зазора; H₁ и H₂ — напряженности поля в теле магнита и в зазоре. Для упрощения примем поле однородным и в магните, и в зазоре. Заметим, что в последних равенствах и дальше в настоящем параграфе под Н мы подразумеваем не модуль вектора Н, который всегда положителен, а алгебраическую величину, которая может быть положительной или отрицательной в зависимости от того, совпадает направление вектора Н с направлением положительного обхода или ему противоположно.

В общем случае неоднородного поля следует написать: F₁ = - F₂, где F₁ и F₂ — магнитодвижущие силы вдоль оси магнита и вдоль оси зазора.

На рис. 55, б изображена часть гистерезисной петли, снятая при большом магнитном насыщении для замкнутого кольца, т.е. при отсутствии зазора, и характеризующей материал магнита; В_r — остаточная индукция; Н_с — коэрцитивная сила. Ветвь abс называется кривой размагничивания. На рис. 55, в эта ветвь перестроена п координатах F и Ф, причем F — МДС вдоль оси магнита, при однородном намагничивании равная H₁l₁, Ф — поток в нейтральной зоне магнита, при однородном намагничивании равный B₁s₁, где s₁ — поперечное сечение магнита.

При отсутствии зазора В = В_r, Ф = Ф_r и Н всюду равно нулю. При наличии зазора на проведение магнитного потока через зазор, имеющий магнитное сопротивление R_M2, требуется МДС F₂ = R_м2Ф₂.

Если считать приближенно поле в зазоре однородным, то

На рис. 55, в прямая OL изображает связь между F₂ и Ф. Так как F₁=-F₂, то прямая ОМ, дающая связь между F₁ и Ф₁; является зеркальным отражением прямой OL относительно оси ординат.

Очевидно, точка b пересечения луча ОМ с кривой размагничивания аbс и определяет магнитное состояние вещества магнита при наличии воздушного зазора.

Энергия магнитного поля в зазоре магнита определяется выражением: ФF₂/2, которое для однородного поля приобретает вид:

где V₂ — объем зазора.

Эта энергия пропорциональна половине площади прямоугольника AbGO на рис. 55, в. Необходимо так проектировать намагничивающее устройство, чтобы эта площадь была максимальной. Соответственно точка b должна занимать на кривой размагничивания в координатах H и В (рис. 55, б) такое положение, чтобы произведение получилось наибольшим.

Трудность расчета таких цепей заключается в вычислении магнитного сопротивления R_m2 пути потока по воздуху с учетом неоднородности поля, учета потока рассеяния, выходящего через боковые поверхности магнита, и определение магнитного состояния при неоднородном намагничивании.

Если в воздушный зазор магнита внести деталь из магнитомягкого вещества, которое легко намагничивается в сравнительно слабых полях, то можно пренебречь магнитным сопротивлением детали и утверждать, что внесение такого тела эквивалентно уменьшению зазора и магнитного сопротивления зазора. Соответственно вместо прямой ОМ будем иметь прямую ОМ' (рис. 56). Однако магнитное состояние магнита не переходит в точку b' по кривой размагничивания, а переходит в точку k по кривой bmk, и магнитный поток увеличивается до значения Ф_k. Если вновь удалить деталь из воздушного зазора, то магнитное состояние вернется в точку b по кривой knb. Петля bmknb носит наименование частной петли гистерезиса.

Если учесть конечное магнитное сопротивление детали, то вместо прямых ОМ и ОМ' будем иметь кривые ON и ON' (рис. 56, б).

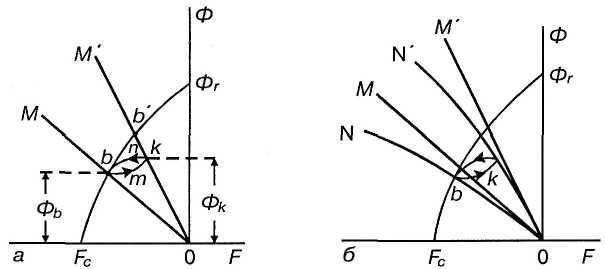
Рис. 56. К оценке магнитного состояния ферромагнитной детали в постоянном магнитном поле.

Отрезки, параллельные оси OF, между кривыми ON и ОМ и между кривыми ON' и ОМ' представляют в масштабе по оси абсцисс значения МДС вдоль намагничиваемой детали при соответствующих значениях магнитного потока. Их можно получить из кривых намагничивания деталей. Вершины b и k частной петли гистерезиса лежат при этом на кривых ON и ON'. Магнитостатика деталей с разветвленной конфигурацией

Часто детали, подвергаемые магнипорошковому контролю, имеют сложную геометрию, поэтому намагничивание отдельных частей зависит от формы тока, материала, взаимного расположения элементов детали и т.п.

Для любого узла разветвленного магнитопровода в установившемся магнитном состоянии справедлив первый закон Кирхгофа

т.е. алгебраическая сумма магнитных потоков в любом узле магнитной цепи равна нулю. Другими словами, суммарная величина магнитных потоков, входящих в узел, равна суммарной величине магнитных потоков, выходящих из узла детали:

Если из этого равенства исключить значение магнитной индукции, то, оказывается, можно сравнивать не магнитные потоки, а величины сечений объемов, в которых магнитный поток имеет противоположные направления.

Для симметричной детали суммарная величина сечений всех объемов, по которым магнитный поток входит в узел, равна суммарной величине сечений всех объемов, по которым магнитный поток выходит из узла (рис. 57, 58).

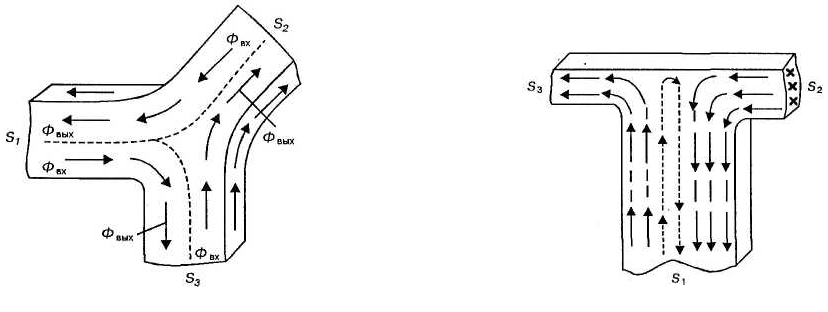
Рис. 57. Узел детали, образованный Рис. 58. Узел детали, образованный

перемычками неравного сечения. перемычками равного сечения.

От соотношения между величинами сечений перемычек, образующих узел детали и от их числа во многом зависит картина магнитного состояния. При образовании узла несколькими перемычками величина сечения одной из них S_i может быть больше суммы сечений всех остальных:

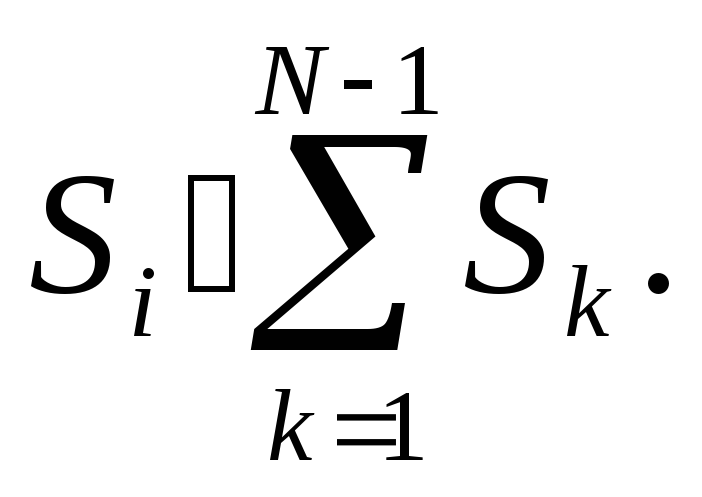
В этом случае эта перемычка в установившемся магнитном состоянии никогда не будет полностью намагниченной (рис. 58) и не может быть проконтролирована хорошо.

Для того чтобы сечение исследуемой перемычки узла было бы полностью намагничено, необходимо выполнение неравенства:

т.е. величина сечения исследуемой перемычки детали должна быть равна или меньше суммы сечений всех остальных перемычек детали.

В случае узла детали, образованного тремя перемычками, что наиболее часто встречается в деталях машин, это равенство при любых величинах сечений S₁, S₂, S₃ может быть преобразовано к виду:

|S₂ - S₃| ≤ S₁ ≤ S₂ + S_3.

Если это условие выполняется, то любая из перемычек этой структуры может находиться в одном из двух полностью намагниченных состояний (+Ф_r или –Ф_r).

В зависимости от конфигурации, условий механического нагружения магнитной структуры, от ее магнитной предыстории в установившемся магнитном состоянии могут иметь место несколько противоположно намагниченных объемов с различными величинами магнитных потоков, замыкающихся по различным путям (рис. 57...59). Все сказанное выше в равной мере может быть отнесено как к плоским, так и к объемным деталям. При реальных магнитных материалах ширина границы между противоположно намагниченными слоями (рис. 60) детали может иметь довольно ощутимую величину, часто соизмеримую с шириной перемычек, что требует первый закон Кирхгофа для магнитных цепей.

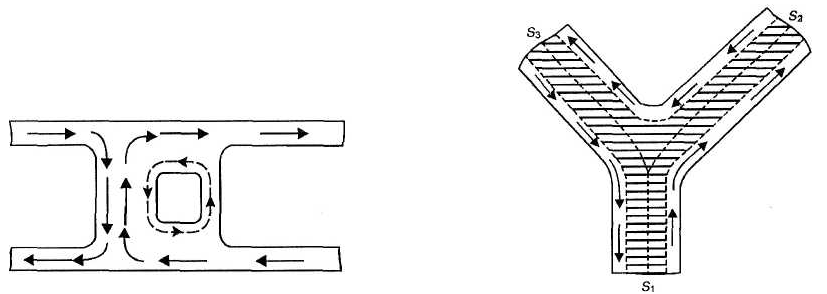
Рис. 59. Картина магнитных потоков Рис. 60. Картина состояния узла,

в разветвленном магнитопроводе. послойное намагничивание.

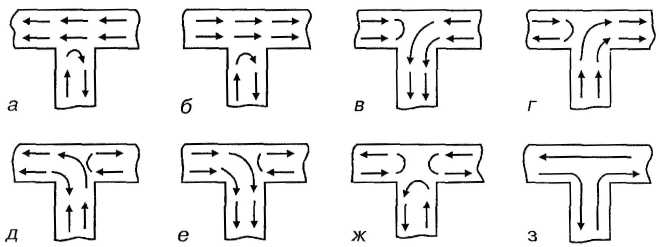
Рис. 61. Устойчивые магнитные состояния симметричного троичного узла.

Поэтому детали в ниде разветвленных конструкций перед выполнением дефектоскопии должны рассматриваться с учетом распределения магнитного потока.

О статической картине распределения магнитного потока в разветвленной детали можно судить на основании измерения ЭДС, наводимых в измерительных катушках, навиваемых на эти части детали.

Узлы, образованные тремя ветвями (рис. 61, 62), наиболее часто встречаются в исследуемых деталях. При симметричном троичном узле две ветви находятся в намагниченном состоянии, третья обязательно в размагниченном.

При несимметричном троичном узле детали сечения ветвей могут иметь различные величины. Встречаются такие троичные несимметричные узлы, сечения двух ветвей которых равны между собой, а сечение третьей равно сумме первых двух. Такие узлы могут иметь два рабочих установившихся магнитных состояния. Узлы четвертичные также могут быть симметричными и несимметричными и магнитное состояние отдельных ветвей может иметь как минимум три варианта.

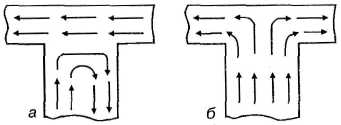
Рис. 62. Устойчивые магнитные состояния несимметричного троичного узла.

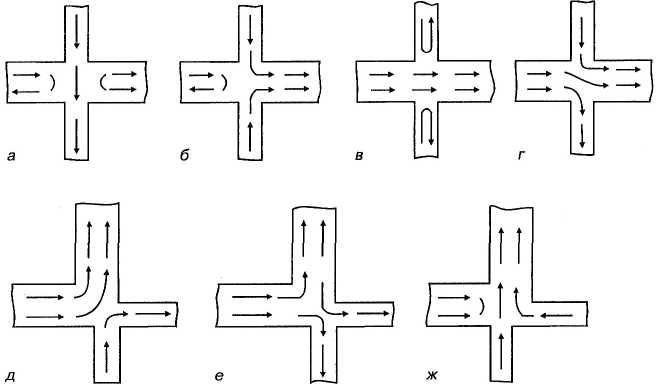
Рис. 63. Некоторые возможные магнитные состояния распределения противопотоков в несимметричных узлах.

На рис. 63 показано семь возможных вариантов распределения магнитных потоков в четвертичном несимметричном узле сложной детали с одним источником МДС.

Картина магнитного состояния узла определяется не только его конструкцией, но и режимом намагничивания.

Перемагничивание от одной МДС

разветвленной детали

Перемагничивание такой детали проходит в определенной последовательности, зависящей от ее конфигурации и размеров по кратчайшему из возможных путей. Однако в зависимости от магнитного состояния отдельных перемычек детали этот путь магнитного потока может быть не самым коротким. Если отдельные пути насыщены, то перемагничивание вначале будет проходить по одному контуру, а затем будет продолжаться по какому-то другому из возможных кратчайших путей перемагничивания. Причем максимальная суммарная величина изменения магнитного потока по сечениям всех контуров не может быть больше изменения магнитного потока в потокозадающей перемычке. Если же величина потокозадающей МДС недостаточно большая, то процесс перемагничивания может закончиться раньше, не изменив магнитного состояния части детали. Создаваемая величина напряженности магнитного поля в этом случае будет недостаточно большой для перемагничивания по самым длинным контурам. При изменении местоположения и величины сечения потокозадающей пермычки условия иеремапгачивания, контуры и величины объемов перемаг-мичивания изменятся.

При рассмотрении режимов перемагничиваиия необходимо также учитывать, какой характер имеет потокозадающая МДС: однополярный или двухполярный. При диухполярной импульсной МДС характер процессов перемагничивания, пути и величины объемов могут изменяться, то будет касаться второго и последующих импульсов потокозадающей МДС. Для первого импульса или постоянного намагничивания все рассмотренные выше положения остаются в силе до появления обратной намагничивающей МДС (рис. 64).

Таким образом, при намагничивании сложной детали для расположения источника МДС следует выбирать места, имеющие самое большое сечение. Величина МДС должна быть регулируемой. Последовательность магнитного контроля отдельных элементов этой детали определяется анализом магнитного состояния этих элементов.

Рассмотрим процесс перемагничивания трехдырочной детали (рис. 65, а) с учетом нелинейности намагничивания. По мере роста МДС граница начала перемагничивания, как и в тороидальной детали, постепенно перемещается от внутренних слоев к наружным. Вслед за этой границей от внутренних слоев к наружным начинает перемещаться граница процесса перемагничивания. Ширина перемагничивающейся области в этом случае определяется качеством магнитного материала, т.е. коэффициентом вертикальности β = H_s / H_p.

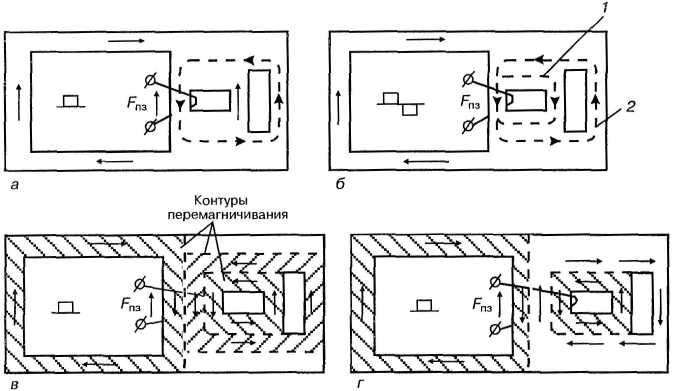
Рис. 64. Коммутация магнитного потока при одной перемагничивающей МДС: 1— путь перемагничивания от второго и последующих импульсов; 2—путь перемагничивания от первого импульса.

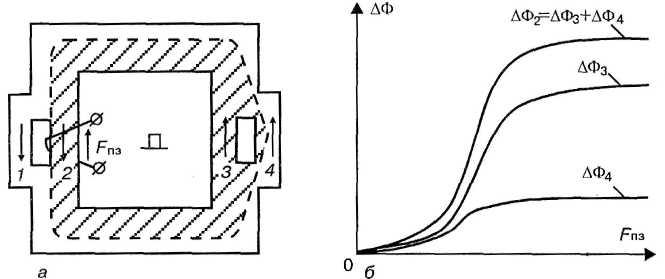
Рис. 65. Картина распределения магнитного потока в разветвленном магнитопроводе с учетом нелинейности кривой намагничивания.

В рассматриваемой конструкции детали в виде разветвленного магнитопровода границы начала и конца области перемагничивания достигают в первую очередь края самых узких участков, т.е. края потокозадающей перемычки 2 и края перемычки 3 (рис. 65). Объем перемагничивания в этом случае становится асимметричным: с одной стороны, ширина зоны перемагничивания ограничена сечением потозадающей перемычки 2, а с другой — ширина зоны перемагничивания не ограничивается только сечением перемычки 3. Однако величина изменения магнитного потока в перемагничиваемом объеме на всех его участках одна и та же. На рис. 65, б показан характер изменения магнитного потока в перемычках 2, 3 и 4 в зависимости от величины потокозадающей МДС F_из. Величина изменения магнитного потока в перемычке 4 будет тем меньше, чем меньше коэффициент вертикальности магнитного материала β = H_s/H_р и чем больше различие в длинах путей перемагничивания 2-3-2 и 2-4-2.

Таким образом, импульсное намагничивание деталей сложной геометрии должно просчитываться с учетом магнитных свойств, геометрических размеров отдельных элементов магнитной цепи, частоты следования импульсов.