I. Общие представления о магнетизме

Суммарный магнитный поток, пронизывающий все витки, называется потокосцеплением контура.

Если все витки одинаковы, то суммарный магнитный поток, т.е. потокосцепление:

где — магнитный поток через один виток; — число витков. Поэтому, потокосцепление соленоида, например, при индукции В=0,2 Т, количестве витков соленоида и сечении окна соленоида дм² будет Вб.

Абсолютная магнитная проницаемость измеряется в единицах «генри на метр» .

Магнитная проницаемость вакуума в системе единиц СИ принята равной Гн/м.

Отношение абсолютной магнитной проницаемости к магнитной проницаемости вакуума называется относительной магнитной проницаемостью .

Соответственно значению  все материалы делятся на три группы:

• диамагнитные, у которых 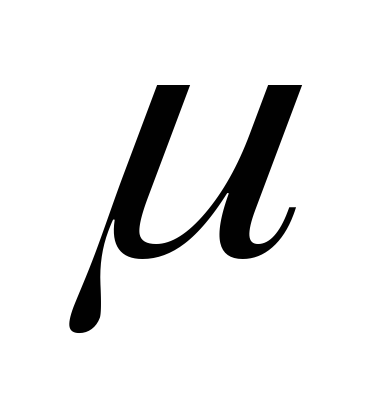на несколько тысячных долей меньше 1. К ним относятся: висмут, цинк, свинец, медь, серебро, золото, воск, большая часть солей;

• парамагнитные, у которых  на несколько тысячных долей больше 1. К таким материалам относятся: марганец, хром, платина, алюминий и др.;

• ферромагнитные, у которых  велико, выражается сотнями и изменяется в зависимости от величины магнитного поля. К таким веществам принадлежат железо, никель, кобальт, гадолиний и некоторые сплавы металлов.

Если диа- и парамагнитное вещества поместить в однородное магнитное поле, то в диамагнитном — поле будет ослабляться, а в парамагнитном — усиливаться. Это объясняется тем, что в диамагнитном веществе поля элементарных токов направлены навстречу внешнему полю, а в парамагнитном — согласно ему.

В табл. 1 приведены значения относительной магнитной проницаемости некоторых материалов. Видно, что значения относительной магнитной проницаемости диамагнитных и парамагнитных материалов очень мало отличается от единицы, поэтому для практики принимают их магнитную проницаемость, равной единице.

• Магнитный контроль применим только для деталей из ферромагнитных материалов, имеющих (ГОСТ 21105-87).

• МП контролю подвергаются конструкционные стали, относительная магнитная проницаемость которых составляет 70... 16000.

Размерность напряженности поля Н (табл. 2):

.

1 А/м — это напряженность такого магнитного поля, индукция которого в вакууме равна Тл.

Таблица 1. Относительная магнитная проницаемость некоторых материалов

Парамагнитные		Диамагнитные		Ферромагнитные
Воздух	1,00000036	Висмут	0,999825	Сталь Армко	7000
Олово	1,000001	Графит	0,999895	Пермаллой	75000
Алюминий	1,000023	Сурьма	0,999937	Ст. Э1ААБ	15400
Платина	1,000364	Серебро	0,999981	Электротехническая сталь	14400
Марганец	1,0037	Медь	0,999991	Никель	1120
Палладий	1,00069	Ртуть	0,999975	Кобальт	174
		Цинк	0,999981	Чугун	620

Иногда напряженность поля измеряют также в

• «эрстедах» (Э),

• «амперах на сантиметр» (А/см),

• «килоамперах на метр» (кА/м).

Соотношение между этими величинами следующее:

1 А/см = 100 А/м; 1 Э = 0,796 А/см; 1 кА/м = 10 А/см;

1 А/см = 0,1 кА/м; 1 Э = 79,6 А/см; 1 кА/м = 12,56 Э;

1 А/см = 1,256 Э; 1 Э = 0,0796 кА/см; 1 кА/м = 1000 А/м.

Интересно знать значения напряженности некоторых магнитных полей.

• Напряженность поля Земли в районе Москвы составляет 0,358 А/см.

• Напряженность поля для намагничивания деталей из конструкционных сталей составляет 100...200 А/см,

• на полюсах постоянного магнита — 1000...2000 А/см.

Иногда пользуются так называемым магнитным моментом контура с током . Он равен произведению силы тока на площадь , ограниченную контуром (рис. 4).

При делении магнита на части каждая из них представляет собой магнит с двумя полюсами. Это видно из рис. 5. По данным табл. 2 можно определить, что одна единица магнитного момента равна 1м² = 1. Эта единица называется «ампер-квадратный метр». Амперквадратный метр — это магнитный момент контура, по которому течет ток силой 1 А и который ограничивает площадь, равную 1 м².

Рис. 4. Контур (1) с током ; Рис. 5. Деление постоянного магнита на части.

2 — источник тока:

— магнитный момент;

— напряженность поля.

Таблица 2. Основные и производные единицы измерений системы СИ, применяемые в неразрушающем контроле

Основные единицы СИ
Величина		Размерность		Единица
				наименование		обозначение
						русское		международное
Длина		L		метр		м		m
Масса		М		килограмм		кг		kg
Сила электрического тока		I		ампер		А		A
Количество вещества		N		моль		моль		mol
Сила света		J		кандела		кд		cd
Производные единицы СИ, имеющие собственные наименования
Величина	Единица
	наименование		обозначение				Величина производной единицы через основные единицы СИ
			русское		международное
Частота	герц		Гц		Hz
Сила	ньютон		Н		N
Давление	паскаль		Па		Ра
Энергия	джоуль		Дж		J
Мощность	ватт		Вт		W
Поток магнитной индукции	вебер		Вб		Wb
Магнитная индукция	тесла		Тл		T
Индуктивность	генри		Гн		H
Количество электричества	кулон		Кл		C
Электрическое напряжение	вольт		Е		V
Электрическая емкость	фарад		Ф		F
Электрическое сопротивление	ом		Ом		Ω
Электрическая проводимость	сименс		См		S
Световой поток	люмен		лм		lm
Активность радионуклида	беккерель		Бк		Bg
Поглощенная доза излучения	грэй		Гр		Gy
Эквивалентная доза излучения	зиверт		Зв		Sv

Магнитный момент электрона равен , так как , а _, .

Относительно недавно взаимодействие полюсов магнитов объясняли наличием особого вещества — магнетизма. С развитием науки было показано, что никакого вещества не существует. Источником магнитных полей являются электрические токи. Поэтому при делении постоянного магнита в каждом куске электронные токи создают магнитное поле (рис. 5). Магнитный заряд рассматривают только как некоторую математическую величину, не имеющую физического содержания.

Единицу магнитного заряда можно получить по формуле:

_{, ,}

где — работа по обводу магнитного полюса вокруг проводника током .

Одна условная единица магнитного заряда будет _.

В системе Гаусса за единицу магнитного заряда принимают такую величину, которая действует на равный магнитный заряд на расстоянии 1 см в вакууме с силой, равной 1 дине.

Способность материалов намагничиваться объясняется существованием в них токов:

• вращение электрона вокруг ядра в атоме,

• вокруг собственных осей (спин электрона) и

• вращение орбит электронов (прецессия электронных орбит) (рис. 6).

Ферромагнитный материал состоит из малых областей (с линейными размерами около 0,001 мм), в которых элементарные токи направлены самопроизвольно. Эти области самопроизвольной намагниченности называют доменами. В каждом домене образуется результирующее поле элементарных токов.

В размагниченном материале магнитные поля доменов направлены хаотично и компенсируют друг друга так, что результирующее поле в детали практически равно нулю.

В результате внешнего воздействия поля отдельных областей (доменов) устанавливаются по направлению внешнего поля и таким образом образуется сильное поле намагниченной детали.

Следовательно, намагниченность — это степень согласованной ориентировки магнитных полей доменов в металле, или иначе, это индукция, создаваемая элементарными токами.

Поскольку элементарные токи обладают магнитными моментами, то намагниченность также определяют как отношение суммарного магнитного момента тела к его объему, т.е.:

.

Намагниченность измеряется в «амперах на метр» (А/м).

Знакопеременное нагружение структуры металла, например в продолжительно работающих турбинных лопатках, в болтах и т.п. деталях приводит к определенному упорядочению внутреннего магнитного поля в зоне иагружения, к появлению следов этого поля на поверхности детали. Это явление используется для оценки остаточного ресурса, определения механических напряжений.

Намагниченность проверяемой детали зависит от напряженности поля , действующего на эту деталь. Ферромагнитные свойства материала зависят также от температуры. Для каждого ферромагнитного материала существует температура, при которой области спонтанной намагниченности под действием теплового движения разрушаются и ферромагнитный материал становится парамагнитным. Эта температура называется точкой Кюри. Точка Кюри для железа равна 753⁰С. При снижении этой температуры ниже этой точки магнитные свойства восстанавливаются.

Рис. 6. Виды элементарных токов:

• а — движение электрона 1 вокруг ядра 4;

• б — вращение электрона вокруг своей оси;

• в — прецессия электронной орбиты;

2 — направление тока;

3 — направление движения;

5 — электронная орбита;

6 — плоскость электронной орбиты;

7 — направление вращения электрона;

8 — траектория прецессионного движения электронной орбиты.

Индукция результирующего поля детали может быть определена по известной формуле:

,

где — намагниченность, т.е. индукция, создаваемая молекулярными токами; — напряженность внешнего поля. Из приведенной формулы видно, что индукция в детали представляет сумму двух составляющих: — определяемой внешним полем и - намагниченностью, которая также зависит от .

На рис. 7 показаны зависимости _{, и} ферромагнитного материала от напряженности внешнего поля.

Рис. 7. Зависимость магнитной индукции и намагниченности от намагничивающего поля .

Кривая показывает, что при относительно слабых полях намагниченность растет весьма быстро (участок а-б). Затем рост замедляется (участок б-в). Далее рост снижается, кривая переходит в прямую линию в-д, имеющую малый наклон к горизонтальной оси . При этом величина постепенно приближается к своему предельному значению . Составляющая изменяется пропорционально напряженности поля . На рис. 7 эта зависимость показана прямой линией о-е.

Чтобы получить кривую зависимости магнитной индукции от напряженности внешнего поля, необходимо сложить соответствующие ординаты кривых и . Эта зависимость изображается кривой , называемой кривой первоначального намагничивания. В отличие от намагниченности магнитная индукция растет до тех пор, пока растет величина , так как по прекращении роста намагниченности величина продолжает увеличиваться пропорционально .

Перемагничивание детали происходит переменным или периодически изменяющимся по направлению постоянным полем.

На рис. 8 показана полная магнитная характеристика образца — петля гистрезиса. В исходном состоянии образец размагничен. Ток в обмотке увеличивают по прямой 0-8. Напряженность поля, создаваемого этим током, изменяется по прямой 0-1. При этом индукция и намагниченность в образце будут увеличиваться по кривым первоначального намагничивания 16 и 17 до точек 16' и 17', соответствующим магнитному насыщению, при котором все магнитные поля доменов направлены по внешнему полю.

При уменьшении тока по прямой 8-9 напряженность поля уменьшается по 1-0 (рис. 8, а). При этом индукция и намагниченность изменяются до значения .

При увеличении тока в отрицательном направлении по 9-10 напряженность поля также увеличивается в отрицательном направлении по 0-2, перемагиничивая образец.

В точке 6 индукция , так как , т.е. . Напряженность поля, соответствующая точке 6, называется коэрцитивной силой по индукции.

В точке 4 намагниченность _{, а .}

Напряженность поля, соответствующая точке 4, называется коэрцитивной силой Н_си по намагниченности. При магнитном контроле считают коэрцитивную силу .

При дальнейшем увеличении напряженности поля до точки 2 индукция и намагниченность достигают наибольших отрицательных значений и (точки 16" и 17"), соответствующих магнитному насыщению образца. При уменьшении тока по прямой 10-11 индукция и намагниченность примут значения, соответствующие .

Таким образом, в результате изменения внешнего поля по 0-1, 1-0, 0-2, 2-0 (рис. 8), а магнитное состояние образца изменяется по замкнутой кривой — петле магнитного гистерезиса.

Рис. 8. Зависимость индукции и намагниченности от напряженности (а), изменение тока в обмотке намагничивания (б).

По петле магнитного гистерезиса определяют следующие характеристики, используемые при магнитном контроле:

Н_т — максимальная напряженность магнитного поля, при которой достигается состояние насыщения образца;

В_r — остаточная индукция в образце после снятия поля;

Н_с — коэрцитивная сила — это напряженность магнитного поля, которое нужно приложить встречно намагниченности образца, чтобы его полностью размагнитить;

В_т — индукция технического насыщения. Принято считать В_т=0,95B_max, где B_max — теоретически возможная индукция насыщения первоначального намагничивания.

Если ферромагнитное тело подвергается действию полей одного знака, то петля гистерезиса, которая в этом случае несимметрична относительно начала координат, называется частной (рис. 9).

Различают статическую и динамическую петли гистерезиса.

Статической петлей гистерезиса называется петля, полученная при медленном изменении Н, при котором можно пренебречь действием вихревых токов.

Динамической петлей гистерезиса называется петля, полученная при периодическом изменении Н с некоторой конечной скоростью, при которой влияние вихревых токов становится значительным. Это приводит к тому, что динамическая петля имеет значительно большую ширину, чем статическая. С увеличением амплитуды приложенного напряжения ширина динамической петли гистерезиса увеличивается.

На рис. 10 показана зависимость . При Н=0 магнитная проницаемость равна ее начальному значению.

Рис. 9. Несимметричные петли гистерезиса 1-3 — промежуточные петли; 4 — предельная петля; 5 — кривая начального намагничивания.

По кривой намагничивания В(Н) абсолютная магнитная проницаемость в заданном поле Н определяется как , а относительная как .

Часто упоминают дифференциальную магнитную проницаемость:

_.

Первая из них равна тангенсу наклона линии 1, а вторая — тангенсу наклона касательной 2.

Магнитодвижущая сила (МДС) равна F = Iw, произведению тока I в обмотке на ее число витков.

Магнитный поток равен:

где F — МДС, измеряемая в ампер-витках; l_ср — длина средней линии магнитопровода, м; S — сечение магнитопровода, м².

Величина определяет магнитное сопротивление R_m.

Рис. 10. Магнитные проницаемости , и индукция В в зависимости от напряженности поля : _{, ;} .

Магнитный поток прямо пропорционален току I и обратно пропорционален магнитному сопротивлению R_m. Допустим, надо определить силу тока в тороидной обмотке из 10 витков кабеля для намагничивания кольца подшипника при индукции 1 Тл.

• Сечение кольца 5 см²,

• наружный диаметр 200 мм,

• внутренний диаметр 170 мм,

• Гн/м.

Используя формулу Ф = F/R_m, найдем:

1. 

2. 

3. 

4. 

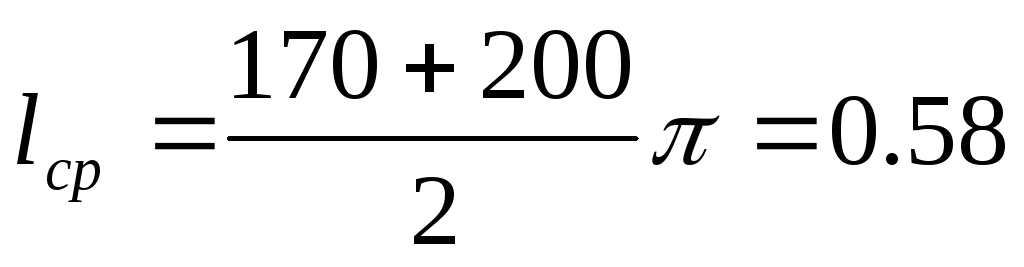
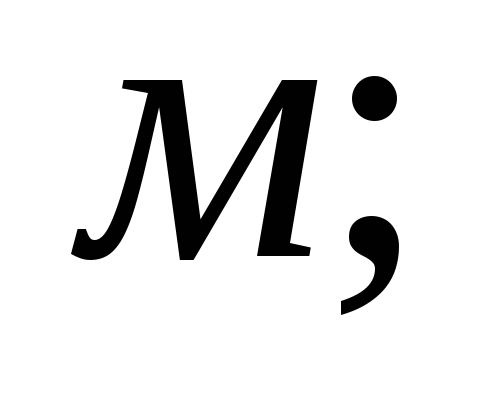
5. Для намагничивания кольца подшипника до индукции 1 Тл (10000 Гс) необходим ток силой 461,7 А, если число витков 10.

Картина поля вокруг проводника представляет собой концентрические окружности с центрами на оси проводника (рис. 11).

Рис. 11. Картина распределения порошка (а) и индукции вокруг проводника с током (б)

Направление поля вокруг проводника или созданного витками кабеля соленоида может быть определено по правилу буравчика.

Если расположить штопор вдоль оси проводника и вращать его по часовой стрелке так, чтобы его поступательное движение совпало с направлением тока в проводнике, то направление вращения ручки штопора укажет направление поля.

Изменение напряженности поля Н внутри и вне проводника 3 при прохождении по нему постоянного тока от расстояния от точки измерения до оси проводника радиусом показано на рис. 12.

Рис.12. Распределение напряженности поля Н внутри (1) и вне (2) проводника с током.

Откуда видно, что поле на оси проводника равно нулю, а внутри проводника (при > ) оно изменяется по линейному закону:

_,

а вне его (при > ) по гиперболе , где — расстояние от оси проводника до точки измерения, м; — ток в проводнике, А.

Если задана напряженность поля H в точке, находящейся на расстоянии от оси провода, то для получения этой напряженности силу тока определяют, используя формулу:

,

где H [А/м], [м].

Если проводник с током проходит через полую деталь, например, кольцо подшипника, то в отличие от предыдущего случая резко растет индукция в зоне ферромагнитной детали (рис. 13).

Рис. 13- Индукция при намагничивании детали при пропускании тока по центральному проводнику.

Поле изменяется на участках: 0-1 по закону Н =0; 1-2 по закону _{; 2-3 по закону .}

Магнитная индукция B изменяется: на участке 0-2 по закону _{; на участках 2-3; 6-7 по закону .}

Скачки индукции В на участках 3-4; 5-6 обусловлены ферромагнетизмом детали 8 ( — радиус проводника; — расстояние от центра проводника).

Допустим, что цилиндрическую полую деталь намагничивают центральным проводником. Определить силу тока в проводнике для получения индукции В = 12,56 мТл на внутренней поверхности детали диаметром 80 мм.

Силу тока в проводнике определим по формуле:

Распределение поля внутри и вне полой детали 4, намагничиваемой пропусканием по ней тока, показано на рис. 14. Видно, что поле внутри детали радиусом R₁ равно нулю. Поле на участке 1-2 (внутри материала детали) изменяется по закону

а на участке 2-3 — по закону . По этой формуле определяют напряженность поля на внешней поверхности детали или на некотором расстоянии от нее.

Рис. 14. Распределение поля Н внутри и вне детали.

Если по цилиндрической детали диаметром 50 мм пропускают ток силой 200,0 А и надо определить напряженность поля в точках, находящихся от поверхности детали на расстоянии 100 мм. Напряженность поля на расстоянии 100 мм от поверхности детали определяется по формуле:

_.

Напряженность поля на поверхности детали составит:

_.

На рис. 15 показана схема магнитного поля вокруг и внутри соленоида. Из рисунка видно также, что магнитные силовые линии внутри соленоида направлены вдоль его продольной оси. У выходных окон соленоида образуются магнитные полюсы N и S.

Напряженность поля в центре на оси у края соленоида определяют по приведенным формулам.

Напряженность поля в центре витка радиусом R определяют по формуле H = I/R, А/м, где I — ток в витке проводника, А.

Если надо определить напряженность поля в центре приставного соленоида с током 200 А, и при этом число витков w = =-6, длина 210 мм, диаметр 100 мм, то напряженность поля будет:

_.

Если в соленоиде ток равен 200 А, а длина соленоида 400 мм, диаметр 100 мм, число витков 8, , (см. рис. 15), то можно вычислить напряженности в отдельных точках соленоида.

Распределение напряженности поля внутри соленоида складывается:

а — в центре соленоида:

_,

где Н — напряженность поля в центре соленоида, А/см; l, с — длина и радиус соленоида, см; w — число витков;

б — на оси соленоида:

_,

где l — длина соленоида, см;

в — у края соленоида:

_,

где l , с — длина и радиус соленоида, см; w — число витков.

Напряженность поля, создаваемая током в тороидной обмотке: , А/см; I — ток, А; l — длина средней линии обмотки, см; w — число витков. В данном примере:

а) напряженность Н₁, в центре на оси соленоида:

б) напряженность поля в точке А — Н₂:

в) напряженность поля у края соленоида — Н₃:

Если диаметр витка равен 160 мм при общем токе, равном 180,0 А, то напряженность поля в центре витка будет:

Рис. 15. Магнитное поле соленоида и распределение напряженности в его центре (а), на оси (б) и у края (в).