Конспект по ТАУ / My laboratory work po TAY / Губеня а

Мета роботи: навчитись моделювати електричні машини і інші електротехнічні пристрої в якості типових динамічних ланок лінійних автоматичних систем.

В якості математичних моделей електромеханічних об’єктів були дослідженні:

1. Генератор постійного струму (ГПС), який має таку математичну модель:

В режимі неробочого ходу для ГПС вхідним сигналом даної моделі є напруга збудження (Uзб), а вихідним – ЕРС обмотки якоря (Еа).

;

;

;

;

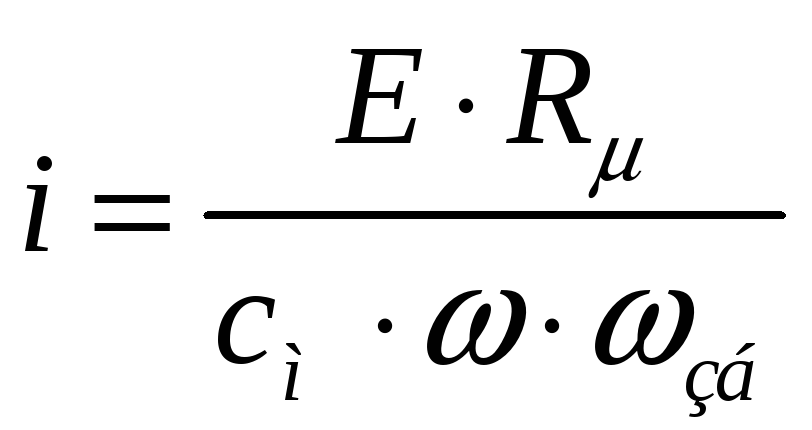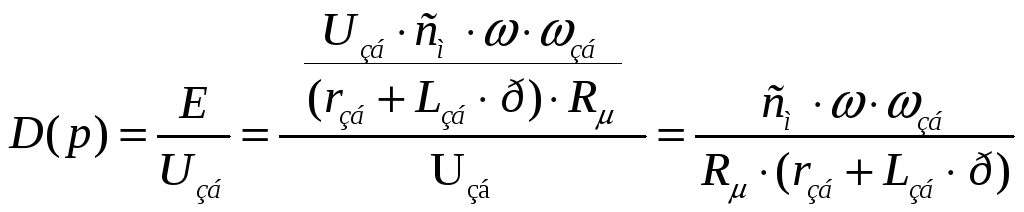
Структурна схема матиме вигляд аперіодичної ланки 1-го порядку:

Рис.1 реакція ланки на функцію Хевісайда

Рис.2 амплітудно-фазо-частотна характеристика для заданого ГПС

2.Автономний синхронний генератор.

У вихідному рівнянні рівноваги кола збудження

1)

Повне потокозчеплення обмотки збудження

Враховуючи що

Множимо обидві частини рівняння на

2)

Розглянемо що становлять складові цього рівняння

та

,

Де коефіцієнт підсилення

Якщо коефіцієнт при похідній у рівнянні 2) помножити та поділити на ,то одержимо р-ння

3)

Із векторної діаграми можемо отримати такі рівняння

тобто

З іншого боку

З урахуванням, що одержимо вираз похідної

Поділимо обидві частини рівняння на

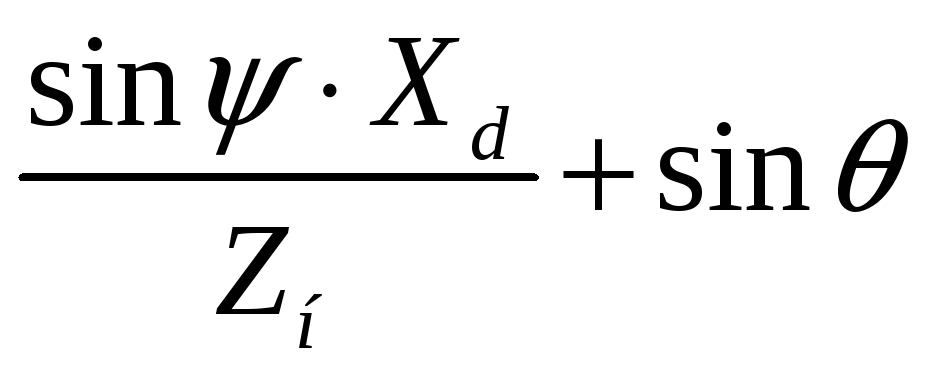
Оскільки це теж аперіодична ланка, то характеристики вона має такі ж як і ГПС

3. ДПС. Розглянемо базову систему рівнянь рівноваги по всім силовим колам:

- коло якоря

- магнітне коло

- механічне коло

- коло збудження

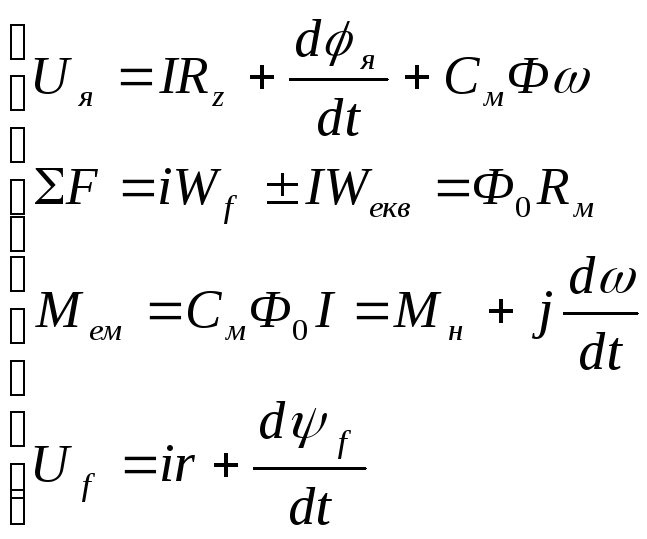
В системах безперервного керування найбільш поширені 2 методи: якірне, у якому керуючим вхідним сигналом є напруга на якорі, та полюсне, у якому керуючим сигналом є напруга на обмотці збудження. Розглянемо побудову моделей для обох варіантів.

При якірному керуванні:

При умові, що Мн прямує до 0, або Мн =const, та розглядаючи струм якірного кола як суму статичної та динамічної складової струму ія, а також потокозчеплення якірної обмотки як , можемо згорнути вироджену с-му р-нянь:

та одержати математичну модель у канонічній формі:

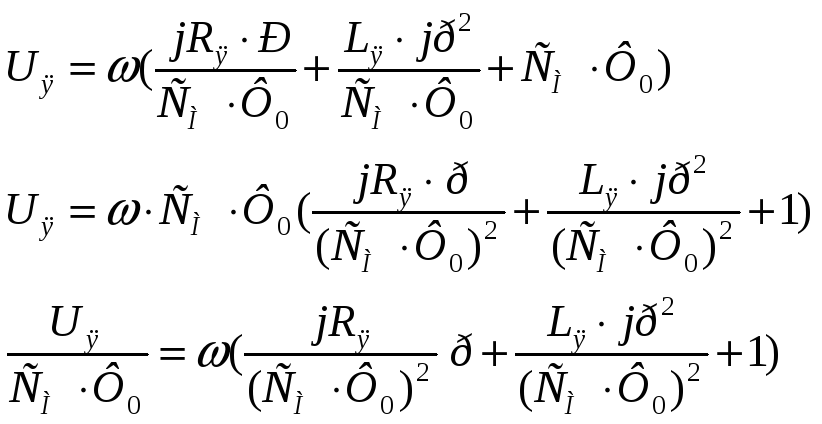
де коефіцієнт передачі (підсилення);

, , с- електромеханічна та електромагнітна стала часу.

Подібний вузол, як відомо має потенційно-коливалний характер перехідноо процесу і відповідає типовій коливальній елементарній ланці, але ланці з типовою не лінійністю типу зони не чуттєвості і тільки за умови нехтуванням впливом напруги зрушення Uзр=ІстRя лінійну найпростішу S-модель двигуна використовуючи блок передавальної ф-ції:

При якірному керуванні:

Головна позитивна якість цього методу це зменшена потужність системи керування і відповідні техніко-економічні переваги.

Загальна систем рівноваги у цьому разі структурно-нелінійна, оскільки окрім змінних коефіцієнтів, у першу чергу магнітного опору Rµ, у рівняння входять співмножники невідомих змінних типу CмФІ та CмФ. Тому лінеаризація системи за умов максимального спрощення можлива тільки при розгляді малих прирощень, що дозволяє згорнути систему до передавальної функції:

де у якості вхідних і вихідних сигналів розглядаються малі прирощення напруги збудження ∆Uf та частоти обертання ∆ відносно заданого усталеного режиму.

Приймемо k=4; T1=0.05; T2=0.08; T3=0.1;; Тоді передавальна функція: D=k./(T1*T2*T3*jw.^3+(T1*T2+T2*T3)jw.^2+(T1+T2)*jw+1);

Структурна схема матиме вигляд аперіодичної ланки 1-го порядку:

Рис.1 реакція ланки на функцію Хевісайда

Рис.2 амплітудно-фазо-частотна характеристика для заданого ДПС

Висновки:

В даній лабораторній роботі ми змоделювали генератор постійного струму в якості аперіодичної ланки, автономний синхронний генератор,в якості аперіодичної ланки і двигун постійного струму в якості диференціюючої ланки. Визначили систему рівнянь рівноваги. За допомогою пакету Simulink побудували реакції передавальних функцій досліджуваних об’єктів на ступінчасту вхідну дію. Обчислили та побудували 6 амплітудно-фазо-частотні характеристики досліджуваних об’єктів.

Отже можна зробити висновок, що за допомогою типових динамічних ланок лінійних автоматичних систем можна легко моделювати електричні машини та інші електротехнічні пристрої.