Червоно-чорні дерева
Додавання вершини
Додавання вершини в червоно-чорне дерево проводиться за час O(logn). Спочатку, як це робилося для двійкових дерев пошуку, ми застосовуємо процедуру insertNode, і фарбуємо нову вершину в червоний колір. Після цього треба відновити RB-властивості, для чого потрібно перефарбувати деякі вершини і виконати обертання. При цьому можливі різні ситуації. Розглянемо їх.
Червоно-чорні дерева
Додавання вершини
RB-INSERT(T, x) |
|
|
|
11 |
|
|
|
||
1. |
insertNode ( x–>key); |
|
|
2 |
|
|
|
|
14 |
2. |
x–>color = RED; //фарбуємо у червоний колір |
1 |
7 |
|
|
y |
|
||
3. |
while( x != root[T] && x–>p–>color = = RED) |
|
5 |
8 |
|
|
|
||
4. |
{ |
|
|
x 4 |
|
|
|
|
Випадок 1 |
|
|
|
|
|
|
||||
5. |
if (x–>p == x–>p–>p–>left)//якщо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6. |
{//батько вершини х є лівою дитиною свого батька |
11 |
|
||||||
7. |
у = x–>p–>p–>right; |
|
|
|
y |
||||
|
|
2 |
|
|
|
|
|||
8. |
if (y–>color = = RED) |
|
|
|
x |
14 |
|||
|
|
1 |
|
|
|||||
9. |
{ |
|
|
7 |
|
|
|
||
|
|
5 |
|
|
|
|
8 |
||
10. |
x –>p–>color = black; //Випадок 1 |
|
|
|
|
|
|||
|
4 |
|
|
|
|
|
|||
11. |
y–>color = black; //Випадок 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
12. |
x–>p–>p–>color = RED; //Випадок 1 |
|
|
|
|
|
|
Випадок 2 |
|
13. |
x = x–>p–>p //Випадок 1 |
|
|
|
11 |
|
|
|
y |
14. |
} |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
x |
7 |
|
|
|
|
14 |
||
15. |
else if( x = = x–>p–>right) |
|
8 |
|
|
|
|
15 |
|
|
2 |
|
|
|
|
||||
16. |
{ |
1 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
||||
17. |
{ x = x–>p; //Випадок 2 |
|
4 |
|
|
|
Випадок 3 |
||
18. |
rotateLeft (Т,x); } //Випадок 2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
19. |
x –>p–>color = black; //Випадок 3 |
|
|
|
7 |
|
|
|
|
20. |
x–>p–>p–>color = RED; //Випадок 3 |
x |
|
|
|
|
|
11 |
|
21. |
rotateRight (T, x–>p–>p) //Випадок 3 |
2 |
8 |
|
|
14 |
|||
|
|
|
|||||||
22. |
} |
1 |
|
5 |
|
|
|
|
|
23. |
} |
|
|
4 |
|
|
|
|
|
15
15
15
Червоно-чорні дерева
Додавання вершини
RB-INSERT(T, x)
24.else
25.{
26.у = x–>p–>p–>left;
27.if (y–>color = = RED)
28. |
{ |
29. |
x –>p–>color = black; //Випадок 1 |
30. |
y–>color = black; //Випадок 1 |
31. |
x–>p–>p–>color = RED; //Випадок 1 |
32. |
x = x–>p–>p //Випадок 1 |
33. |
} |
34.else if( x = = x–>p–>right)
35.{
36. |
{ x = x–>p; //Випадок 2 |
37. |
rotateRigth (Т,x); }//Випадок 2 |
38. |
x –>p–>color = black; //Випадок 3 |
39. |
x–>p–>p–>color = RED; //Випадок 3 |
40. |
rotateLeft (T, x–>p–>p) //Випадок 3 |
41. |
} |
42.}
43.}
44.root[T]–>color = BLACK;
Червоно-чорні дерева
Додавання вершини
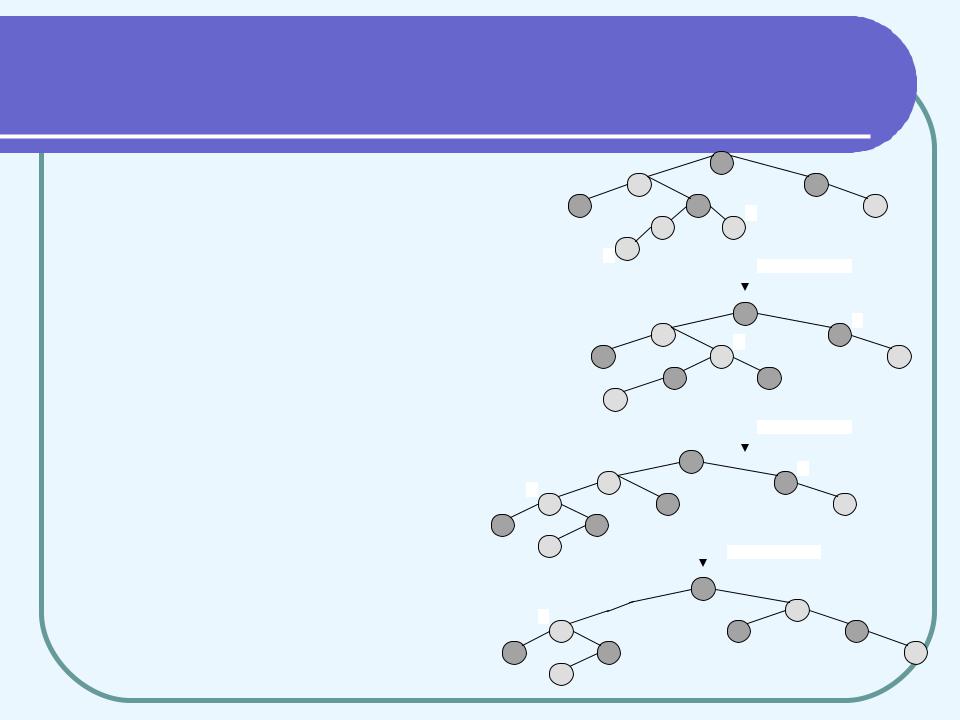
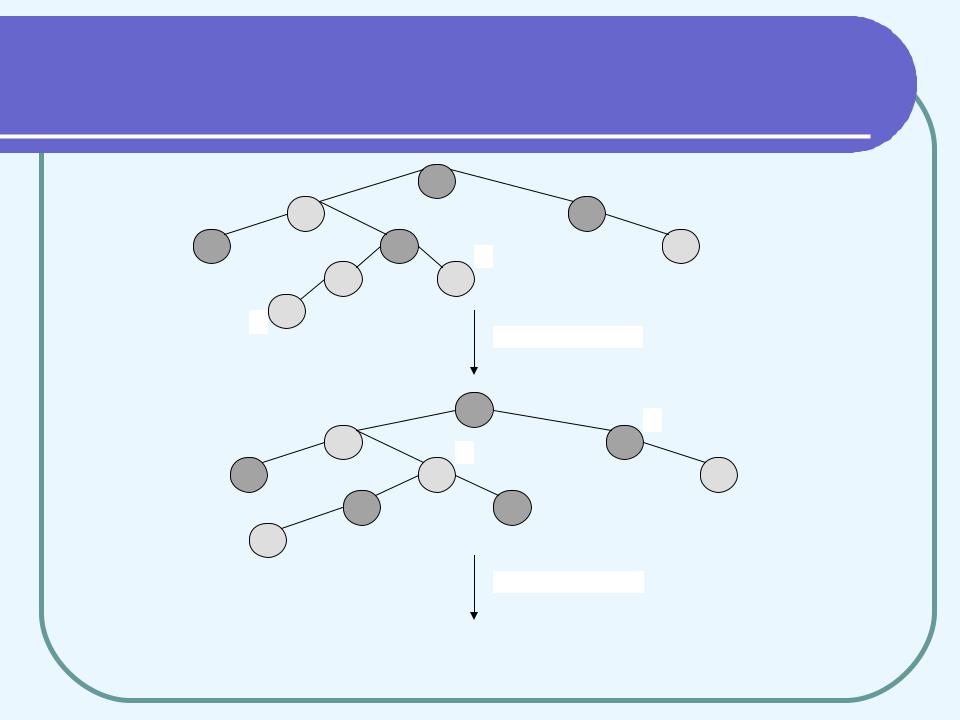
На рис. 4 наведений приклад застосування процедури RB-Insert. Після виконання рядків 1-2 виконуються всі RB-властивості, крім однієї: червона вершина х може мати червоного батька (рис. 4 а). Така ситуація буде зберігатися після будь-якого числа ітерацій циклу. Після кожної ітерації вершина х піднімається нагору по дереву (якщо тільки не вдалося усунути порушення цілком; у цьому випадку ми виходимо з циклу).
Усередині циклу розглядаються шість випадків, але три з них симетричні трьом іншим, розходження лише в тому, чи є батько вершини х лівою або правою дитиною свого батька. Ці випадки розділяються в рядку 5. Рядки 5-23 відносяться до випадку, коли x–>p - ліва дитина свого батька. (Симетричні випадки описуються, починаючи з рядка 24.)
Припускаємо, що всі розглянуті червоно-чорні дерева мають чорний корінь (це підтримується рядком 44). Тому в рядку 5 червона вершина x–>p не може бути коренем (x–>p–>p існує).
Червоно-чорні дерева
Додавання вершини
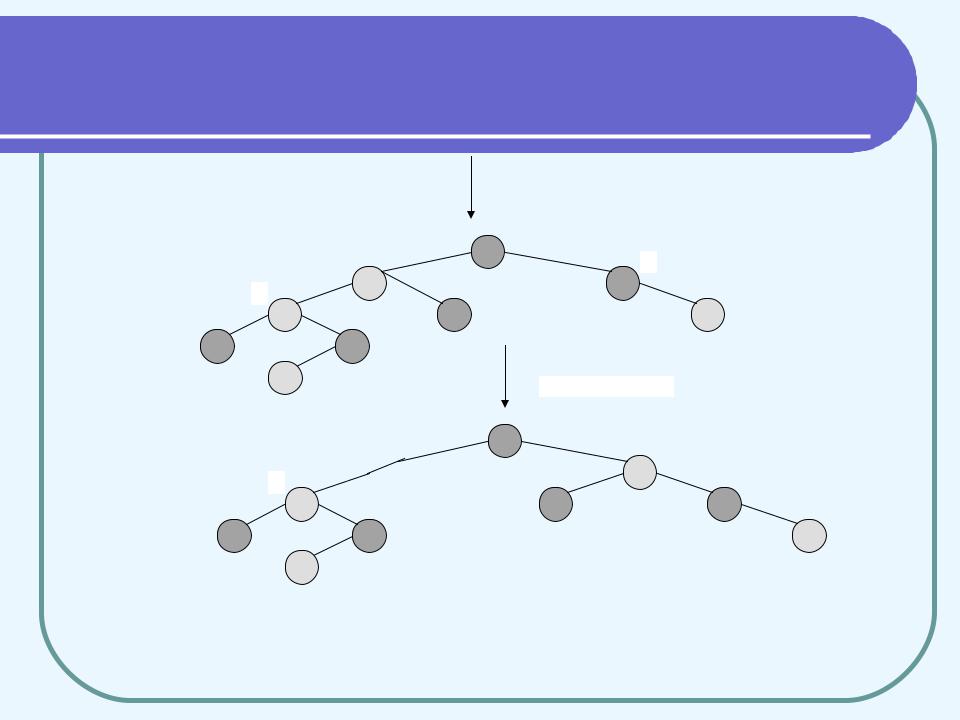
Операції усередині циклу починаються з пошуку вершини y, яка є «дядьком» вершини х (має того ж батька, що і вершина x–>p). Якщо вершина y червона, має місце випадок 1, якщо чорна - то один з випадків 2 або 3. В усіх випадках вершина x–>p–>p чорна, тому що пара x - x–>p була єдиним порушенням RB-властивостей. На рис. 4 а додана вершина х, при цьому порушилася властивість 4: x і її батько червоні. Вершина y - дядько вершини х - червона, тому має місце випадок 1. Після перефарбування вершин одержуємо дерево (б). Нова вершина x і її батько червоні, але дядько y чорний. Так як х - права дитина, має місце випадок 2. Виконується ліве обертання, що дає дерево (в). Тепер уже х є лівою дитиною і це - випадок 3. Після правого обертання одержуємо коректне червоно-чорне дерево (г).
Червоно-чорні дерева
Додавання вершини
а)
б)
|
|
|
11 |
|
|
|
2 |
|
14 |
1 |
|
7 |
y |
15 |
|
|
|
|
|
|
|
5 |
8 |
|
|
x |
4 |
|
|
|
|
|
Випадок 1 |
|
|
|
|
|
|
|
11 |
y |
|
|
|
|
|
2 |
x |
14 |
|
|
|
|
1 |
7 |
|
15 |
|
5 |
|
8 |
|
4 |
|
|
Випадок 2
Рис. 4 Робота процедури RB-Insert
Червоно-чорні дерева
Додавання вершини
в)
г)
|
|
11 |
y |
|
|
|
|
x |
7 |
|
14 |
|
|
|
|
2 |
8 |
|
15 |
1 |
5 |
|
|
4 |
|
|
Випадок 3 |
|
|
|
|
|
|
7 |
|
x |
|
|
11 |
|
|
|
|
|
2 |
8 |
14 |
1 |
5 |
|
15 |
|
4 |
|
|
Рис. 4 Робота процедури RB-Insert
Червоно-чорні дерева
Додавання вершини
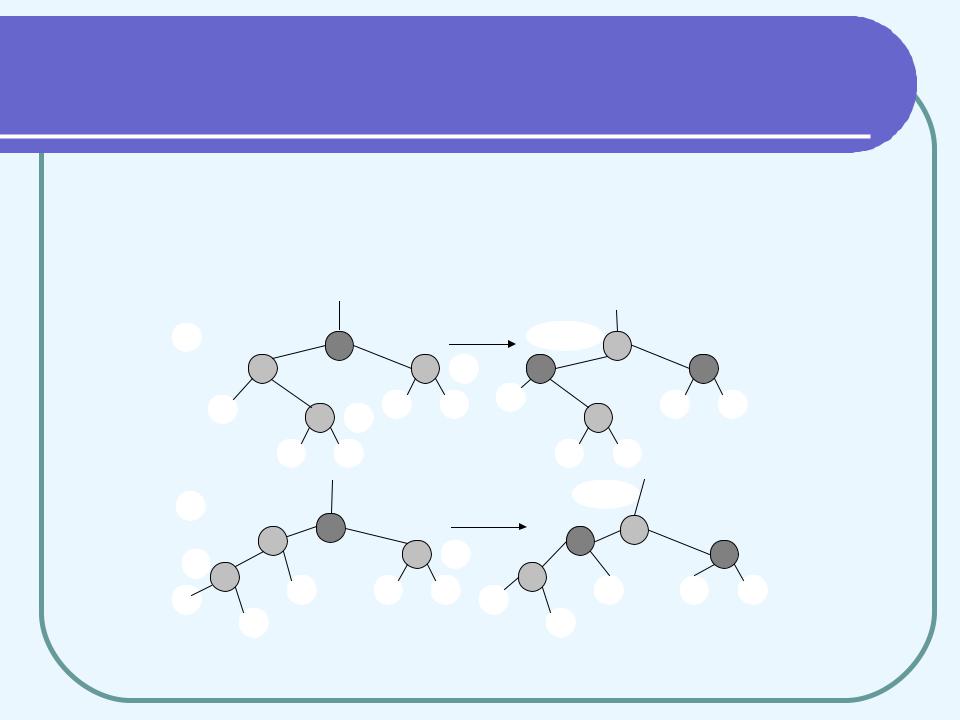
Випадок 1 (рядки 10 - 13) показаний на рис. 5(наші дії не залеж. від того чи х – правий син (а), чи – лівий (б)); обидві вершини x–>p і y червоні, а вершина x–>p–>p чорна. Перефарбуємо x–>p і y у чорний колір, а x–>p–>p - у червоний. При цьому число чорних вершин на будь-якому шляху з кореня до листків не зміниться. Порушення RB-властивостей можливе в єдиному місці нового дерева: у x–>p–>p може бути червоний батько. Тому треба продовжити виконання циклу, і дати х значення x–>p–>p.
(a) |
|
|
C |
|
нове x |
C |
|
|
|
|
|
|
|
|
|
||
|
|
A |
D |
y |
A |
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
B |
x |
|
|
B |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
(б) |
|
|
|
|
|
нове x |
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
C |
|
B |
C |
|
|
|
|
D |
y |
|
|
D |
||
|
x |
|
|
|
|
|||
|
|
|
|
A |
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Рис. 5. Ілюстрація випадку 1.
Червоно-чорні дерева
Додавання вершини
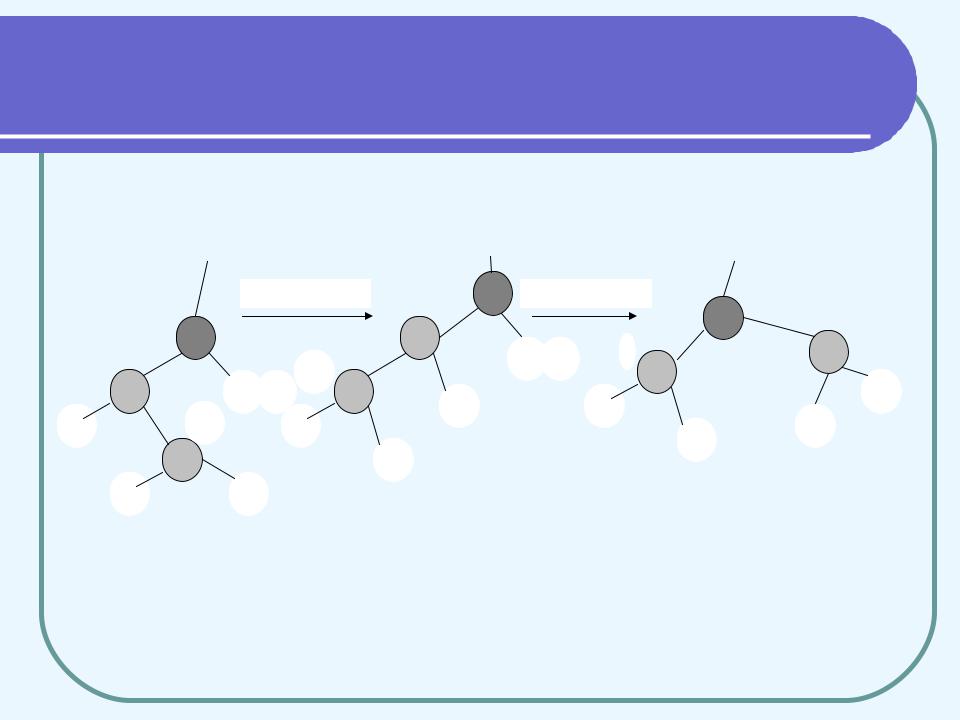
Увипадках 2 і 3 вершина y чорна. Якщо х є правою дитиною свого батька, виконуються
рядки 17-18 (випадок 2). У цьому випадку виконується ліве обертання, яке зводить випадок 2 до випадку 3, коли х є лівою дитиною (рис. 6). Так як і x, і x–>p червоні, після обертання кількості чорних вершин на шляхах залишаються незмінними.
|
Випадок 2 |
C |
Випадок 3 |
|
|
|
|
|
|
|
|
|
B |
|
C |
|
B |
|
x |
C |
|
|
|
|
y |
||
|
|
x |
|
A |
||
|
|
|
|
|
||
A |
y |
A |
|
|
|
|
|
x |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6. Ілюстрація випадків 2 і 3 процедури RB-Insert
Якщо червона вершина х є лівою дитиною червоної вершини x–>p, яка є лівою дитиною чорної вершини x–>p–>p, правою дитиною якої є чорна вершина y (випадок 3), виконується праве обертання вершини x–>p–>p і перефарбовуються дві вершини, щоб усунути порушення RB-властивостей. Цикл більше не виконується, тому що вершина x–>p тепер чорна.
Червоно-чорні дерева
Додавання вершини
Висота червоно-чорного дерева є O(logn), якщо в дереві n вершин, тому виконання RB-Insert вимагає часу O(logn). Цикл повторюється, тільки якщо ми зустрічаємо випадок 1, і при цьому х рухається вверх по дереву. Таким чином, цикл повторюється O(logn) раз, і загальний час роботи O(logn). При цьому виконується не більше двох обертань (після яких ми виходимо з циклу).