13.2.3. Діелектрична проникність та провідність іонізованого газу в реальних умовах

Без врахування зіткнень з важкими частинками, електрон повністю випромінює енергію, отриману від електромагнітної хвилі. Енергія переходить в інший вид та іонізований ідеальний газ.Проте у реальному газі відбуваються постійні зіткнення між зарядженими частинками. Під час кожного зіткнення втрачається частина енергії. Тому відбуваєтьсяпоглинаннярадіохвиль у реальному іонізованому газі. Цей процес можна описати так: під час зіткнення з важкими частинками електрон віддає їм енергію, отриману від електромагнітної хвилі, ця енергія переходить в енергію теплового руху важких частинок. Це можна трактувати як активний опір, що розсіює енергію поля.

Кількісно поглинання можна оцінити через провідність іонізованого газу:

, (13.13)

де – маса електрона,

– частота коливань,

– кількість контактів (зіткнень) носіїв в одиницю часу.

Відносна діелектрична проникність іонізованого газу:

. (13.14)

З цього співвідношення можна зробити висновок, що значення діелектричної проникності іонізованого газу завжди менше від одиниці й залежить від робочої частоти.

Якщо підставити у формули (13.12) та (13.13) значення заряду, маси електрона та діелектричної проникності вільного простору отримаємо:

, (13.15)

. (13.16)

Для високих частот (13.5) та (13.6) проведемо заміну, тоді формули:

, (13.17)

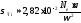. (13.18)

Якщо, то:

, (13.19)

. (13.20)

В цьому випадку електричні параметри іонізованого газу не залежать від частоти.

Частоту, за якої відносна діелектрична проникність дорівнює нулю, називають власною частотою іонізованого газу, абочастотою Ленгмюра:

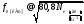. (13.21)

Якщо зіткнень немає, тобто – діелектричну проникність визначає формула (13.17), а питома провідність дорівнює нулю. За відсутності зіткнень іонізований газ можна трактувати як ідеальний діелектрик.

Отже, на основі з’ясованого вище, можемо зробити такі висновки:

– відносна діелектрична проникність іонізованого газу – величина менша за одиницю;

– відносна діелектрична проникність іонізованого газу залежить від частоти;

– відносна діелектрична проникність іонізованого газу залежить від концентрації електронів в одиниці об’єму;

– іонізований газ є дисперсним середовищем, оскільки швидкість поширення хвилі визначає співвідношення:

, де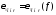. (13.22)

Зауважимо, що за частот, менших , коефіцієнт заломлення – величина уявна. Фізичний зміст такого стану – відсутність коливань. В такому середовищі електромагнітні коливання швидко згасають.

13.3. Заломлення та відбивання радіохвиль в іоносфері

13.3.1. Траєкторія променя в іоносфері

Реальна іоносфера – це неоднорідний іонізований газ. Із висотою змінюється 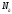, отже, відповідно і(коефіцієнт заломлення), таким чином, що промінь переходить із середовища однієї густини в середовище з меншою густиною. Тобто за неоднорідності іоносфери радіохвилі поширюються не за прямолінійною траєкторією, а за криволінійною. Радіохвиля, що зазнає повне внутрішнє відбиття від іоносфери, повертається на Землю (рис. 13.8):

(13.23)

Рисунок 13.8. Заломлення радіохвилі в іоносфері

Застосування до кожної границі шарів в іоносфері другого закону Снеліуса:

,

надає:

(13.24)

За умови =90° та=1:

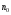. (13.25)

Промінь вертається на Землю, якщо :

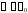. (13.26)

Визначимо граничну частоту, за якої промінь відбивається від іоносфери та повертається на Землю:

(13.27)

Нерівність (13.27) – умова повернення променя за даних та.