
ОПІР
МАТЕРІАЛІВ
Семестр - 2
Лекція - 15
Тонкостінні оболонки

Зміст лекції
Розрахунок осесиметричних тонкостінних оболонок
Визначення напружень
Розрахунок оболонок на міцність
Окремі випадки
Сферичний резервуар під тиском
Циліндричний резервуар під тиском
проф. С.М. Шукаєв |
Опір матеріалів, Лекція №13, |
2 |
2008 р. |

Розрахунок
осесиметричних
тонкостіннихВ різних галузях техніки широко використовуються
деталі і елементи конструкцій, які можна віднести до тонкостінних оболонок. Це резервуари для зберігання нафти, повітряні і газові балони, куполи будинків, корпуси ракет тощо.
проф. С.М. Шукаєв |
Опір матеріалів, Лекція №15, |
3 |
2013 р. |
Розрахунок
осесиметричних
тонкостіннихВизначення напружень
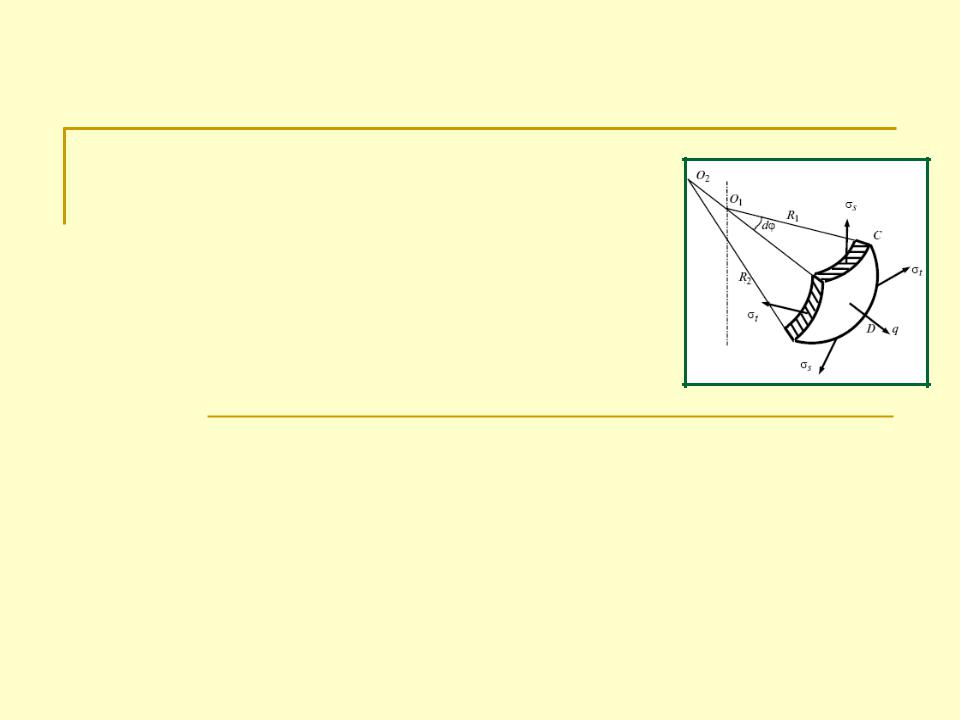
Розглянемо резервуар, що представляє собою осесиметричну оболонку з товщиною стінки h, навантажену внутрішнім тиском p.
Меридіональні перерізи оболонки представляють собою плавні криві без зламів. Перерізи, перпендикулярні осі, – кола. Край оболонки закріплено так, що в перерізі діють тільки нормальні напруження.
проф. С.М. Шукаєв |
Опір матеріалів, Лекція №15, |
4 |
2013 р. |
Розрахунок
осесиметричних тонкостінних оболонок
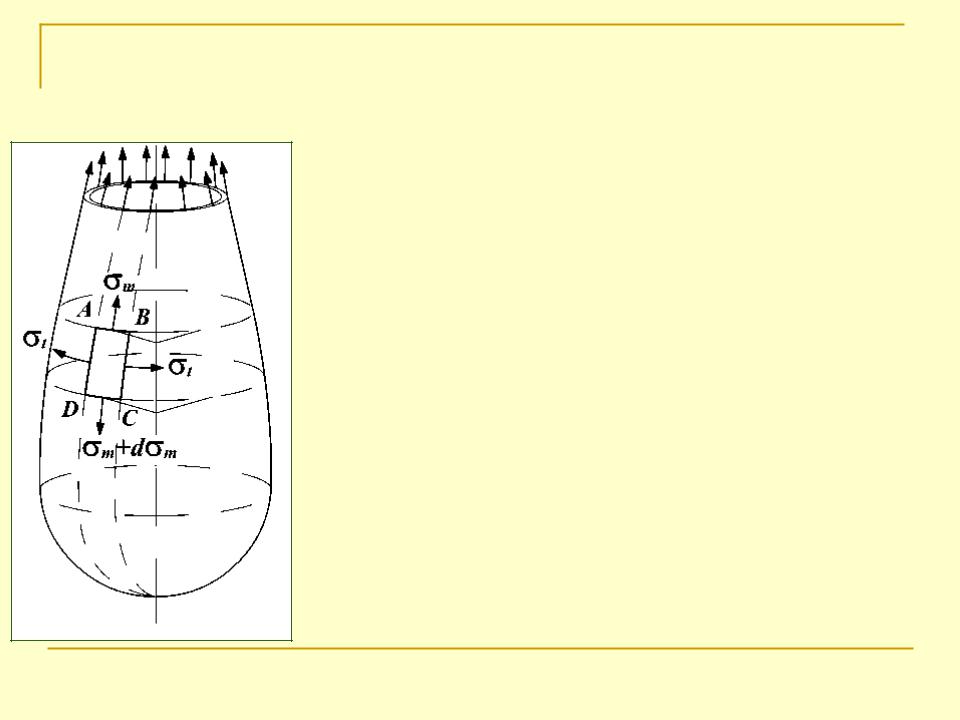
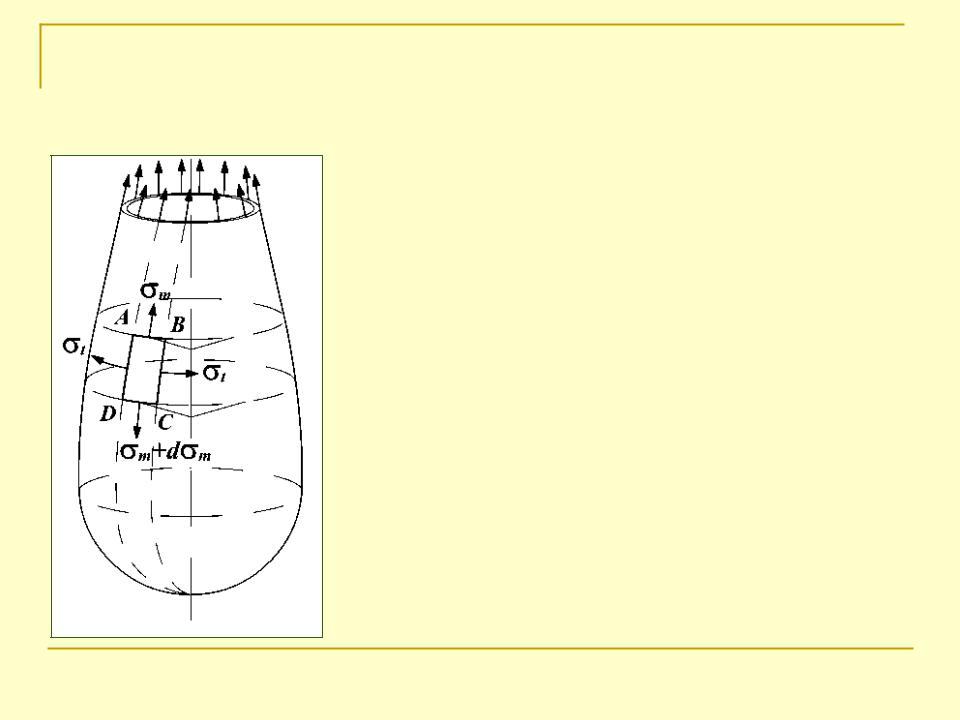
Зі стінки резервуара виділимо елемент ABCD двома площинами, що проходять через меридіани, і двома конічними поверхнями, що пересікають оболонку вздовж паралелей AB, CD.
проф. С.М. Шукаєв |
Опір матеріалів, Лекція №16, |
5 |
2009 р. |
Розрахунок
осесиметричних тонкостіннихПозначимо:оболонок
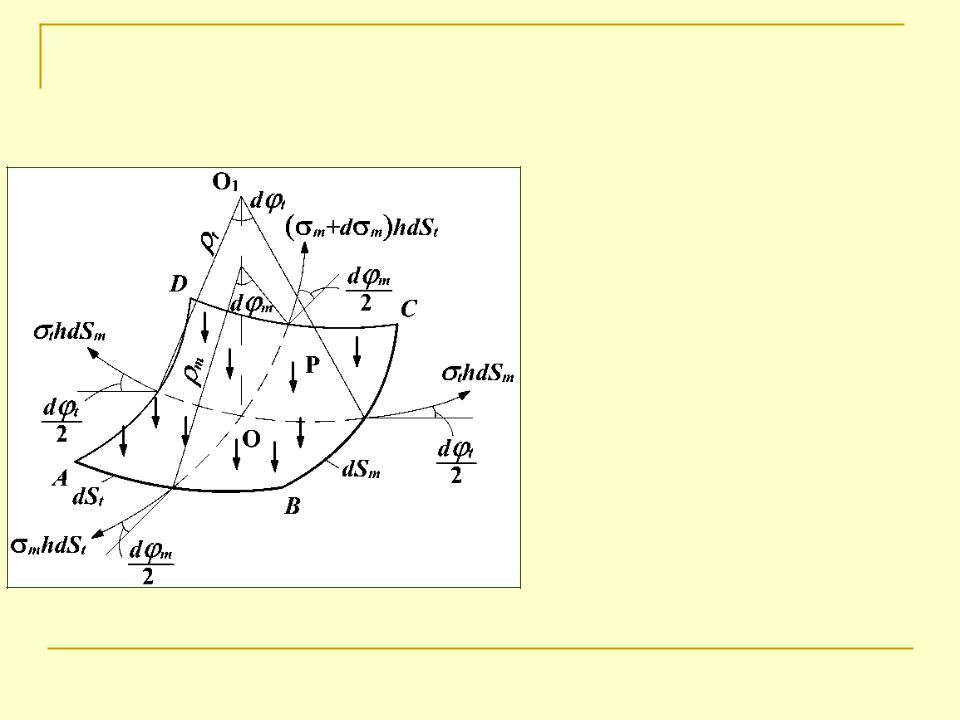
OO1 – нормаль до елемента;
O – центр елемента;
m, t – радіуси кривизни оболонки в меридіональному і тангенціальному напрямах.
проф. С.М. Шукаєв |
Опір матеріалів, Лекція №16, |
6 |
2009 р. |

Розрахунок
осесиметричних
Прикладемотонкостіннихдо елемента зовнішніоболонокі внутрішні сили
і запишемо рівняння рівноваги: сума проекцій сил на нормаль OO1 дорівнює нулю:
2 t hdSm sin d t |
mhdSt sin d m |
m d m hdSt sin d m dSmdSt p 0 |
|||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
Для малих |
sin |
d |
m |
|
d |
m |
|
sin |
d |
t |
|
|
d |
t |
|
d m |
|
dSm |
|
d t |
|
dSt |
|||||||||||
Кутів: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
m |
|
t |
||||||||||||||||||||
|
|
|
|
2 |
|
|
2 |
|
|
2 |
|
|
2 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Звідси: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
hdS |
dSt |
|
2 |
|
|
hdS |
dSm |
d |
|
hdS |
|
dSm |
|
dS |
|
dS |
p 0 |
|||||||||||||||
|
|
|
|
t 2 |
|
|
|||||||||||||||||||||||||||
t |
|
m 2 |
t |
|
|
|
m |
|
|
|
t 2 |
m |
|
|
|
|
m |
|
|
|
|
|
|
m |
t |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 442 4 43m |
|
|
|
|
|
|
|
|
||||||||||
нехтуємо
проф. С.М. Шукаєв |
Опір матеріалів, Лекція №16, |
7 |
2009 р. |
Розрахунок
осесиметричних
Поділившитонкостіннихна hdSmdSt, одержимооболонокрівняння Лапласа:
t m P
t m h
Рівняння містить два невідомихt, m. Меридіональні напруження
знаходять з умови рівноваги частини оболонки.
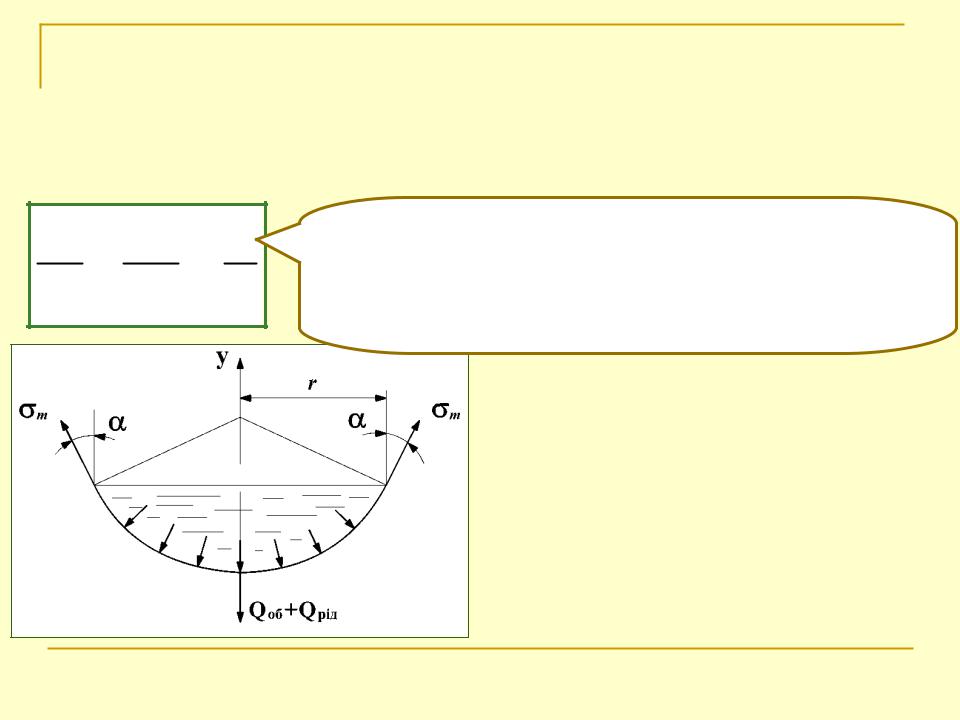
Розглянемо частину оболонки, відсічену конічною поверхнею, нормальною до поверхні оболонки, в якій міститься рідина під тиском.
проф. С.М. Шукаєв |
Опір матеріалів, Лекція №16, |
8 |
2009 р. |
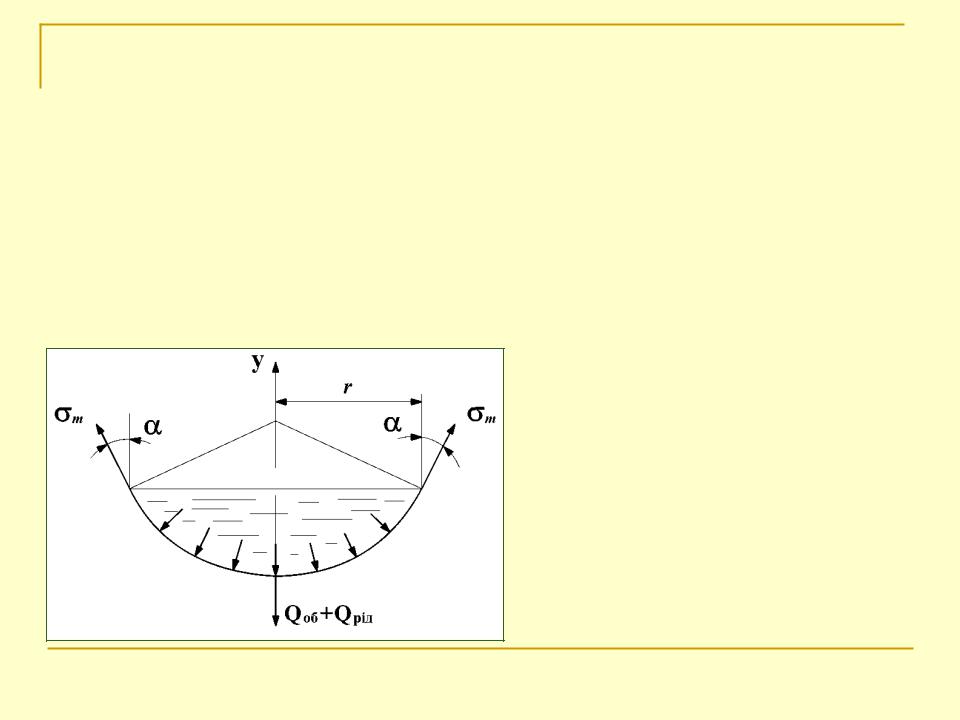
Розрахунок
осесиметричних тонкостіннихПозначимо: оболонок
– кут нахилу меридіональної кривої до осі
оболонки в точці, де визначаються напруження; Qоб,Qрід – вага розглядуваної частини оболонки і
рідини, що в ній міститься; r - радіус оболонки , де визначаємо напруження.
Запишемо умову рівноваги як суму проекцій усіх сил на вісь y:
проф. С.М. Шукаєв |
Опір матеріалів, Лекція №16, |
9 |
2009 р. |

|
|
|
|
|
|
|
|
|
|
||||
|
Розрахунок |
|
|
|
|
||||||||
|
осесиметричних |
||||||||||||
|
|||||||||||||
|
тонкостінних оболонок |
||||||||||||
|
|
|
2 rh cos |
p r2 Q Q |
|||||||||
|
|
mоб |
рід |
|
|
|
|
Qоб Qрід |
|
||||
|
|
Звідси: |
m |
pr |
|
|
|
||||||
|
|
2h cos |
2 rh cos |
||||||||||
|
|
|
|
|
|
|
|
||||||
|
|
Без урахування ваги оболонки і рідини: |
|||||||||||
|
|
|
|
|
|
|
|
|
|
Це рівняння ще |
|||
|
|
m |
|
pr |
|
|
|
|
|||||
|
|
|
|
|
називають рівнянням |
||||||||
|
|
|
|
|
|
|
|||||||
|
|
2h cos |
|
|
|||||||||
|
|
|
|
|
|
|
|
зони. |
|||||
Увага! Оскільки оболонка тонка, то в формули для напружень можна підставляти зовнішні, внутрішні або середні радіуси.
проф. С.М. Шукаєв |
Опір матеріалів, Лекція №16, |
10 |
2009 р. |

Розрахунок
осесиметричних
тонкостіннихРозрахунок оболонок на міцністьоболонок
Напруження t і m є головними, оскільки в перерізах оболонки, де вони діють, в силу симетрії відсутні дотичні напруження. Третє напруження r змінюється від 0 на зовнішній поверхні оболонки до p на внутрішній, але воно набагато менше m і t, тому ним нехтують і вважають, що оболонка знаходиться в умовах плоского напруженого стану.
проф. С.М. Шукаєв |
Опір матеріалів, Лекція №15, |
11 |
2013 р. |
