
- •Оглавление.
- •Микромир атомно-молекулярных масштабов и классическая физика
- •Волны де Бройля и соотношения неопределенностей. Атом Бора.
- •Основы квантовой теории
- •Барьерные задачи
- •Квантовомеханическая модель атома водорода
- •Электромагнитные переходы
- •Многоэлектронные атомы
- •Физика молекул
- •Макроскопические системы.
- •Справочные данные
Основы квантовой теории
Исходя из предположения, что свободной частице с импульсом
 соответствует плоская волна с волновым
вектором
соответствует плоская волна с волновым
вектором (гипотеза де Бройля) и частотой
(гипотеза де Бройля) и частотой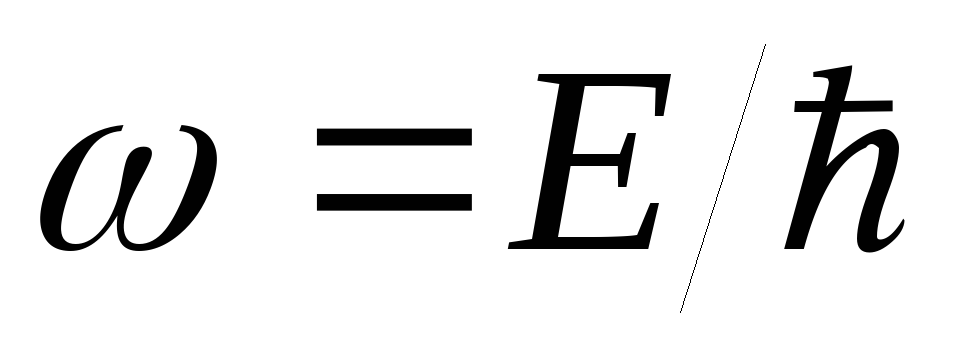 (
( ),
получить нерелятивистское волновое
уравнение, описывающее свободное
движение частицы.
),
получить нерелятивистское волновое
уравнение, описывающее свободное
движение частицы.Используя выражение для релятивистской связи энергии и импульса
 ,
в условиях предыдущей задачи найти
релятивистское волновое уравнение,
описывающее движение свободной частицы.
,
в условиях предыдущей задачи найти
релятивистское волновое уравнение,
описывающее движение свободной частицы.Волновая функция частицы в некоторый момент времени определяется выражением
 .
.
Определить средние значения и дисперсии координаты и импульса частицы в этом состоянии.
Определить средние значения кинетической и потенциальной энергии в основном состоянии а) линейного гармонического осциллятора, б) атома водорода.
Показать, что гауссов волновой пакет минимизирует соотношение неопределенностей.
Определить собственные значения и собственные функции операторов импульса
 ,
, кинетической
энергии
кинетической
энергии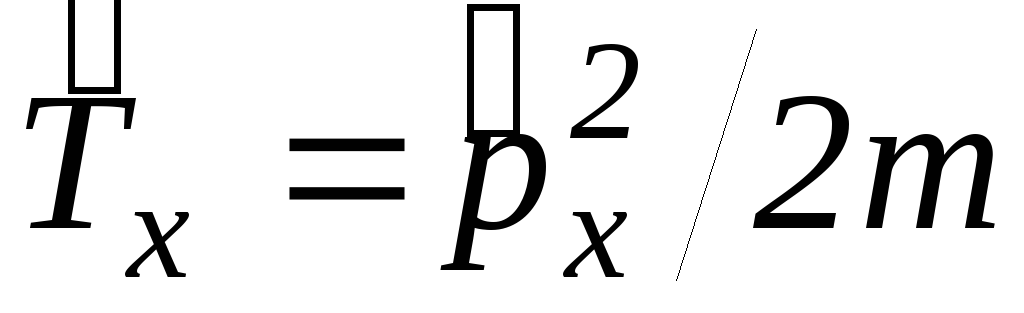 ,
, - проекции момента количества движения
- проекции момента количества движения .
.Может ли так быть, что в одном и том же состоянии импульс и полная энергия имеют точно определенные значения?
Состояние частицы определяется волновой функцией
 .
.
Определить
плотность вероятности распределения
импульса
![]() .
.
Волновая функция некоторой системы в сферических координатах определяется выражением
![]() .
.
Какие
значения z-
проекции момента количества движения
и с какой вероятностью могут быть
измерены в этом состоянии? Каковы среднее
значение и дисперсия величины ![]() ?
?
Волновая функция некоторой системы в сферических координатах определяется выражением
![]() .
.
Какие
значения квадрата момента количества
движения и с какой вероятностью могут
быть измерены в этом состоянии? Каковы
среднее значение и дисперсия величины
![]() ?
?
Частица массы
 находится в одномерной бесконечно
глубокой прямоугольной потенциальной
яме шириной
находится в одномерной бесконечно
глубокой прямоугольной потенциальной
яме шириной .
Написать волновые функции хотя бы двух
состояний, в которых среднее значение
энергии частицы равно
.
Написать волновые функции хотя бы двух
состояний, в которых среднее значение
энергии частицы равно .
.Частица массы
 находится в одномерной бесконечно
глубокой прямоугольной потенциальной
яме шириной
находится в одномерной бесконечно
глубокой прямоугольной потенциальной
яме шириной .
Найти значения
.
Найти значения ,
которые могут быть измерены в этом
состоянии. Какова вероятность их
измерения и среднее значение величины
,
которые могут быть измерены в этом
состоянии. Какова вероятность их
измерения и среднее значение величины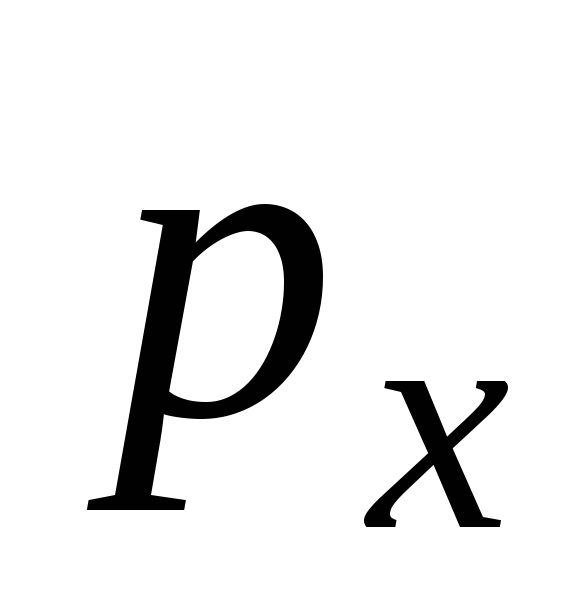 .
.Показать, что для частицы, движущейся в потенциальном поле
 ,
справедливо утверждение (теорема
Эренфеста)
,
справедливо утверждение (теорема
Эренфеста)
![]() .
.
Здесь скобки означают усреднение по квантовому состоянию.
Показать, что для частицы, движущейся в гармоническом потенциале
 ,
изменение во времени среднего значения
координаты
,
изменение во времени среднего значения
координаты
 определяется классическим законом
движения.
определяется классическим законом
движения.Показать, что для частицы, движущейся в потенциальном поле
 ,
среднее по квантовому состоянию
значение импульса удовлетворяет
соотношению
,
среднее по квантовому состоянию
значение импульса удовлетворяет
соотношению .
Здесь
.
Здесь - среднее значение координаты,
- среднее значение координаты, - масса частицы.
- масса частицы.Волновая функция частицы, находящейся в гармоническом потенциале, в момент времени
 определяется выражением
определяется выражением
![]() ,
,
где
![]() .
Определить среднее значение координаты
частицы, как функцию времени.
.
Определить среднее значение координаты
частицы, как функцию времени.
Частица находится в бесконечно глубокой прямоугольной потенциальной яме в состоянии
 ,
, и
и - волновые функции нижних стационарных
состояний,
- волновые функции нижних стационарных
состояний, .
Определить среднее значение и дисперсию
координаты частицы как функцию времени.
.
Определить среднее значение и дисперсию
координаты частицы как функцию времени.Определить энергию нижнего стационарного состояния частицы в одномерной прямоугольной потенциальной яме конечной глубины в случаях: а)
 ,
б)
,
б)  (
(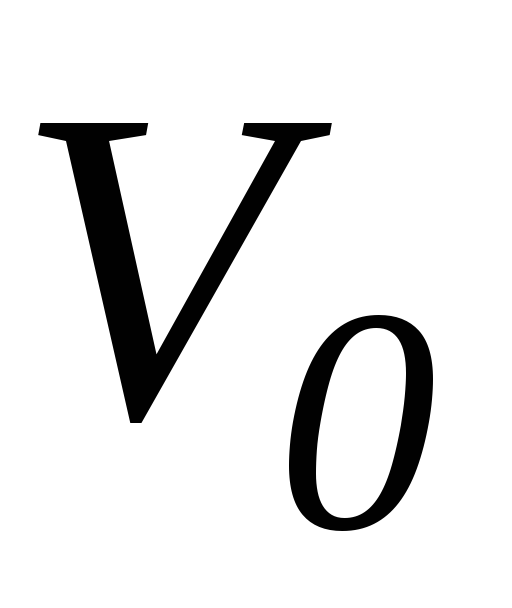 - глубина потенциальной ямы,
- глубина потенциальной ямы,  - ее ширина).
- ее ширина).Частица массы
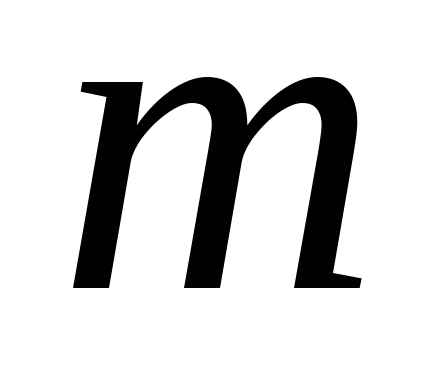 находится в одномерном потенциале
находится в одномерном потенциале
 Определить, сколько связанных состояний
находится в яме в следующих случаях:
а)
Определить, сколько связанных состояний
находится в яме в следующих случаях:
а)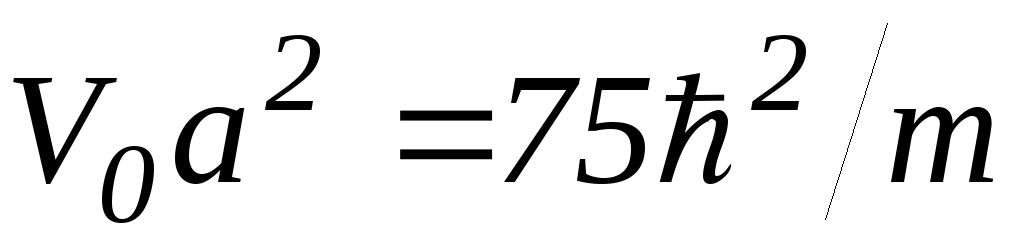 ,
б)
,
б) .
.Показать, что волновая функция системы из двух взаимодействующих частиц может быть представлена в виде произведения волновых функций, описывающих относительное движение частиц и движение центра масс.
Дейтрон имеет энергию связи
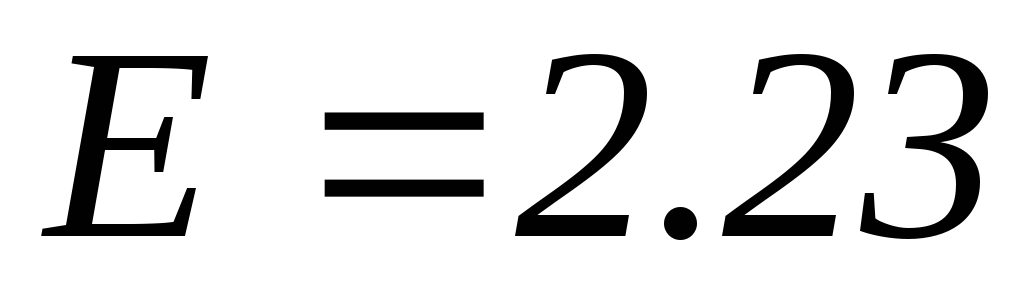 МэВ, среднее расстояние между протоном
и нейтроном
МэВ, среднее расстояние между протоном
и нейтроном см, возбужденного состояния у дейтрона
нет. Используя эти данные, оценить
глубину потенциальной ямы поля ядерных
сил.Указание:
Яму считать прямоугольной, а ее размер
положить равным расстоянию
см, возбужденного состояния у дейтрона
нет. Используя эти данные, оценить
глубину потенциальной ямы поля ядерных
сил.Указание:
Яму считать прямоугольной, а ее размер
положить равным расстоянию
 .
.Определить энергетический спектр и волновые функции стационарных состояний трехмерного изотропного гармонического осциллятора
 .
.Определить энергетический спектр и волновые функции стационарных состояний системы связанных линейных гармонических осцилляторов с гамильтонианом
 ,
где
,
где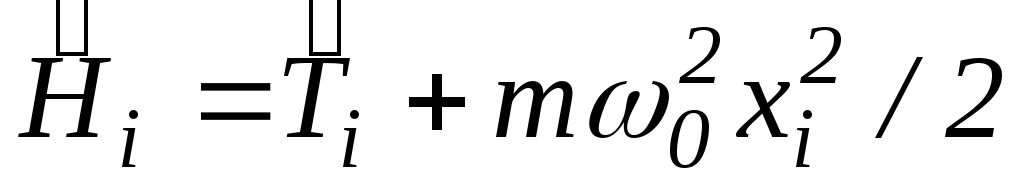 - гамильтониан гармонического осциллятора
с частотой
- гамильтониан гармонического осциллятора
с частотой ,
, - константа связи.
- константа связи.Определить уровни энергии одномерного ангармонического осциллятора
 .
Ангармоническую добавку считать малой.
.
Ангармоническую добавку считать малой.Определить энергии стационарных состояний заряженной частицы, находящейся в гармоническом потенциале
 ,
в присутствие внешнего однородного
постоянного электрического поля.
,
в присутствие внешнего однородного
постоянного электрического поля.Используя теорию возмущений, найти энергию и волновую функцию основного состояния системы из двух связанных линейных осцилляторов, описываемую гамильтонианом
 .
Результат сравнить с точным решением
(см. задачу 3.23).
.
Результат сравнить с точным решением
(см. задачу 3.23).Ядро атома трития
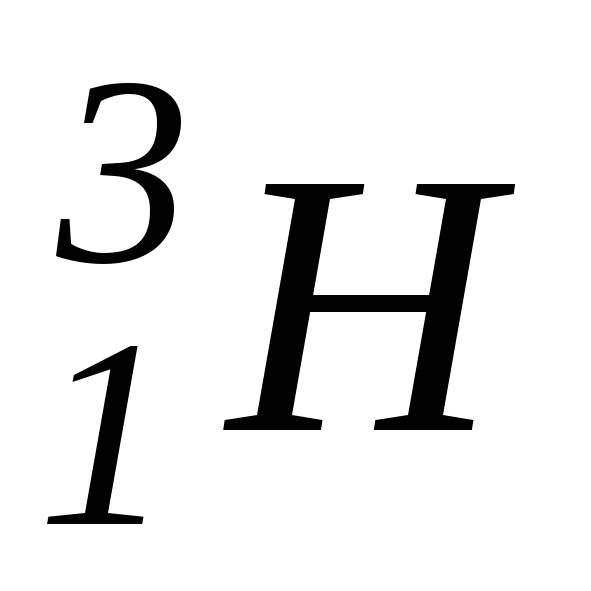 испытывает
- распад с образованием ядра
испытывает
- распад с образованием ядра
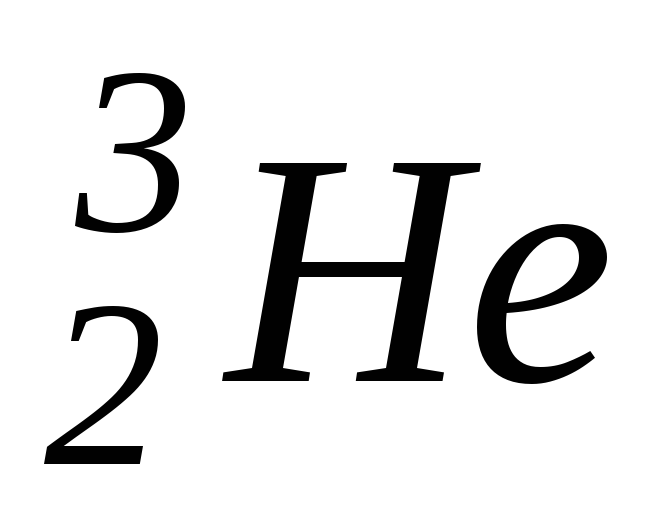 .
Определить вероятность того, что
образующийся водородоподобный ион
гелия будет находиться в основном
состоянии.Указание:
Поскольку образующийся при
- распаде электрон является релятивистским,
изменение заряда можно считать
мгновенным.
.
Определить вероятность того, что
образующийся водородоподобный ион
гелия будет находиться в основном
состоянии.Указание:
Поскольку образующийся при
- распаде электрон является релятивистским,
изменение заряда можно считать
мгновенным.
