
1.2 Отображение Пуанкаре
Существует множество методов исследования нелинейных систем. В данной задаче для исследования применялся один из самых эффективных и информативных методов - отображение Пуанкаре на фазовой плоскости. С помощью отображения Пуанкаре можно отличить друг от друга движения качественно различающихся типов, например: периодические, квазипериодические, хаотические и т.д.
Одним из видов математических моделей динамики является разностное уравнение, иначе называемое отображением. Дадим также другое, более точное, определение понятия отображения при математическом исследовании динамических систем.
Отображением
называют временную выборку данных
{x(t![]() ),x(
),x(![]() ),…x(
),…x(![]() )},для
которой вводят обозначение
)},для
которой вводят обозначение
![]() =
x(
=
x(![]() ).
В простом детерминированном отображении
величину x(n+1)
можно
найти по значению
).
В простом детерминированном отображении
величину x(n+1)
можно
найти по значению
![]() :
:
![]() =f(
=f(![]() ).
(4)
).
(4)
Мы
будем рассматривать отображение Пуанкаре
для систем с вынужденными колебаниями,
тогда если
![]()
![]() x(
x(![]() )и
)и
![]()
![]()
![]() (
(![]() ),то
последовательность точек фазового
пространства будет представлять собой
двумерное отображение:
),то
последовательность точек фазового
пространства будет представлять собой
двумерное отображение:
![]() =
f(
=
f(![]() ,
,![]() )
)
![]() =
g(
=
g(![]() ,
,
![]() )
(5)
)
(5)
Если
моменты выборки
![]() подчиняются
правилу:
подчиняются
правилу:
![]() =
n*T+
=
n*T+![]() (6)
(6)
Где Т - период вынуждающего движения, то это отображение называется отображением Пуанкаре. Перечислим классы структур, встречающиеся в отображениях Пуанкаре:
а) Конечный набор точек - периодическое или субгармоническое колебание.
б) Замкнутая кривая - квазипериодическое движение в присутствии несоизмеримых частот.
в) Фрактальный набор точек - "странный" аттрактор в трехмерном фазовом пространстве.
г) Бесформенный набор точек – Возможны четыре случая:
1) Динамическая система со слишком сильным случайным сигналом или шумом на входе.
2) "Странный" аттрактор, но диссипация в системе очень слаба.
3) "Странный" аттрактор в фазовом пространстве с более чем тремя измерениями.
4) Квазипериодическое движение с тремя или большим числом доминирующих несоизмеримых частот. [4]
Постановка задачи
Дано уравнение движения маятника с колеблющейся точкой подвеса (1).
За начальные условия, приняты следующие величины:
![]() =0,
=0,
![]() =
=![]()
Также начальным параметрам, которые в ходе исследования оставались неизменными, были следующие значения:
![]() =0.25,
=0.25,
![]() =1,
=1,
![]() =1.56
=1.56
Задача
состояла в изучении поведения маятника
при различных значениях амплитуды (![]() )
колебания точки подвеса. Значение
)
колебания точки подвеса. Значение![]() изменялось на интервале[0,3]
с
шагом d
изменялось на интервале[0,3]
с
шагом d![]() = 0.001, от 3 до 5 с шагом 0.1, и
далее от 5 до 8 с шагом 0.3, от 8 до 10 с шагом
0.5.
Исследование
проводилось при помощи фазового портрета
системы и построения отображения
Пуанкаре на фазовой плоскости.
= 0.001, от 3 до 5 с шагом 0.1, и
далее от 5 до 8 с шагом 0.3, от 8 до 10 с шагом
0.5.
Исследование
проводилось при помощи фазового портрета
системы и построения отображения
Пуанкаре на фазовой плоскости.
Физической
моделью данной системы является обычный
физический маятник, точка подвеса
которого совершает гармонические
колебания с амплитудой 2![]() .
Уравнение движения данной системы
представляет собой дифференциальное
уравнение второго порядка. Существует
два способа его решения: аналитический
и численный. Аналитическое решение
(если оно, конечно, существует) очень
сложно, и поэтому задача решалась только
численно. В качестве численного метода
решения задачи использовался метод
Рунге - Кутта четвертого порядка. Алгоритм
решения уравнения этим методом:
.
Уравнение движения данной системы
представляет собой дифференциальное
уравнение второго порядка. Существует
два способа его решения: аналитический
и численный. Аналитическое решение
(если оно, конечно, существует) очень
сложно, и поэтому задача решалась только
численно. В качестве численного метода
решения задачи использовался метод
Рунге - Кутта четвертого порядка. Алгоритм
решения уравнения этим методом:
Сначала
уравнение (1) представляется в виде
системы двух уравнений первого порядка:
![]() =
=![]()
![]() =
=
![]() (7)
(7)
Или
![]() =
=![]() (
(![]() )
)
![]() =
=
![]() (
(![]() )(8)
)(8)
где:
![]() (
(![]() )
=
)
=![]()
![]() (
(![]() )
=
)
=![]()
Далее
по методу Рунге-Кутта вводятся
![]() для
для![]() :
:
![]() =
=
![]() (
(![]() )
)![]()
![]() =
=
![]() (
(![]() )
)![]()
![]() =
=
![]() (
(![]() )
)![]() (9)
(9)
![]() =
=
![]() (
(![]() )
)![]()
и
для
![]() :
:![]() =
=![]() (
(![]() )
)![]()
![]() =
=
![]() (
(![]() )
)![]()
![]() =
=
![]() (
(![]() )
)![]() (10)
(10)
![]() =
=
![]() (
(![]() )
)![]()
Далее
определяем
![]() и
и![]() по формулам:
по формулам:
![]() =
=
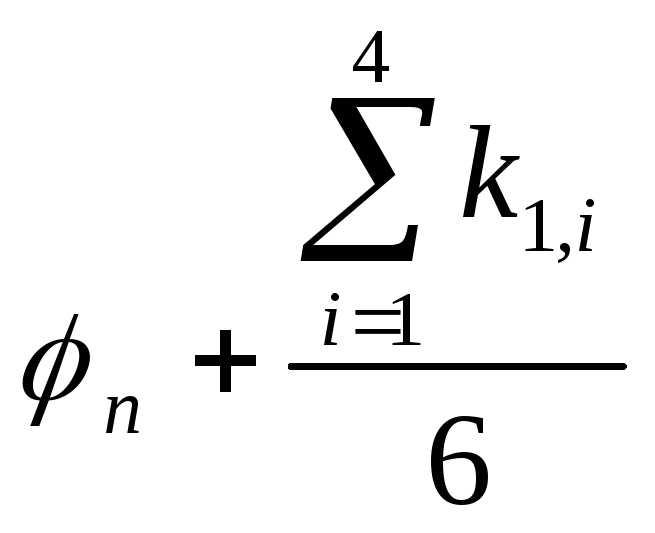 ,
,![]() =
= (11)
(11)
Обсуждение результатов
Анализ
результатов показывает, что при малых
значениях
![]()
![]() [0,
0.354]
колебания являются затухающими. На рис.
1 изображен фазовый портрет таких
колебаний при
[0,
0.354]
колебания являются затухающими. На рис.
1 изображен фазовый портрет таких
колебаний при
![]() =0.15.
=0.15.

рис.1.
![]() =
0.15 – Затухающие колебания
=
0.15 – Затухающие колебания
Далее
при
![]()
![]() [0.
355,0.423]
колебания принимают субгармонический
характер (удвоение периода). Пример
фазового портрета таких колебаний
изображен на рисунке 4.
[0.
355,0.423]
колебания принимают субгармонический
характер (удвоение периода). Пример
фазового портрета таких колебаний
изображен на рисунке 4.
При
![]()
![]() [0.424,0.478]
наблюдаются затухающие колебания.
[0.424,0.478]
наблюдаются затухающие колебания.
При
![]()
![]() [0.479,0.536]
колебания становятся гармоническими.
[0.479,0.536]
колебания становятся гармоническими.
Затем
при
![]()
![]() [0.537,0.587]
вновь наблюдается бифуркация (удвоение)
периода.
На отображении Пуанкаре две точки,
изображенные на Рис. 2, которые означают,
как уже говорилось, удвоение периода.
[0.537,0.587]
вновь наблюдается бифуркация (удвоение)
периода.
На отображении Пуанкаре две точки,
изображенные на Рис. 2, которые означают,
как уже говорилось, удвоение периода.

Рис.
2.
![]() =0.56
– Бифуркация
Периода
=0.56
– Бифуркация
Периода
При
![]()
![]() [0.
588,0.595]
колебания принимают квазипериодический
характер (утроение, учетверение периода).
[0.
588,0.595]
колебания принимают квазипериодический
характер (утроение, учетверение периода).
При
![]()
![]() [0.
596,1.265]
колебания принимают характер странного
аттрактора, отображение Пуанкаре для
которого при
[0.
596,1.265]
колебания принимают характер странного
аттрактора, отображение Пуанкаре для
которого при
![]() =0.65
изображено на рис 3.
=0.65
изображено на рис 3.

рис.3.
![]() =
0.65 - "Странный" аттрактор
=
0.65 - "Странный" аттрактор
В
точке
![]() =
0.
780 наблюдается особое явление переходного
хаоса: при вырождении на отображении
Пуанкаре
восемь
точек. Фазовый портрет системы и
отображение Пуанкаре
для данного случая
изображены на рис. 4,1 и Рис. 4,2.
=
0.
780 наблюдается особое явление переходного
хаоса: при вырождении на отображении
Пуанкаре
восемь
точек. Фазовый портрет системы и
отображение Пуанкаре
для данного случая
изображены на рис. 4,1 и Рис. 4,2.

Рис. 4,1 Отображение Пуанкаре Рис. 4,2 Фазовый портрет
![]() =0.78
- Восьмикратный период
=0.78
- Восьмикратный период
При
![]()
![]() [1.265,
2.159]
колебания становятся периодическими
- на отображении Пуанкаре
-
одна точка.
[1.265,
2.159]
колебания становятся периодическими
- на отображении Пуанкаре
-
одна точка.
При
![]()
![]() [2.160,
2,847]
наблюдаются субгармонические колебания
с двойным периодом.
[2.160,
2,847]
наблюдаются субгармонические колебания
с двойным периодом.
При
![]()
![]() [2.848,
2.885]
наблюдаются квазипериодические колебания
с четверным периодом.
[2.848,
2.885]
наблюдаются квазипериодические колебания
с четверным периодом.
При
![]()
![]() [2.887,
2.888]
наблюдаются квазипериодические колебания
с восьмерным периодом.
[2.887,
2.888]
наблюдаются квазипериодические колебания
с восьмерным периодом.
При
![]()
![]() [2.889,
3]
вновь наблюдался "странный"
аттрактор.
[2.889,
3]
вновь наблюдался "странный"
аттрактор.
Далее
исследования проходили с шагом d![]() = 0.1, отметить можно:
= 0.1, отметить можно:
![]() =3.4
- затухающие колебания.
=3.4
- затухающие колебания.
![]()
![]() [3.5,
5.5]
- субгармонические колебания с двойным
периодом.
[3.5,
5.5]
- субгармонические колебания с двойным
периодом.
![]() ={10.0}
- периодические колебания, Фазовый
портрет показан на рис. 5.
={10.0}
- периодические колебания, Фазовый
портрет показан на рис. 5.
![]() ={9.9;
8.3}
- хаос; динамическая система со слишком
сильным сигналом или шумом на входе.
={9.9;
8.3}
- хаос; динамическая система со слишком
сильным сигналом или шумом на входе.

рис.5.
![]() =10.0
- Периодические колебания
=10.0
- Периодические колебания
Выводы
В
результате выполнения задачи мы
исследовали зависимость характера
колебаний маятника
с колеблющейся (в вертикальной плоскости)
точкой подвеса в зависимости от амплитуды
вынуждающей силы. Были подтверждены
распределения областей
значений нарастающих / затухающих
изображенные на Рис. 1 – при
![]()
![]() [0,
0.354]
и,
затем при
[0,
0.354]
и,
затем при
![]()
![]() [0.424,0.478]
колебания затухающие.
[0.424,0.478]
колебания затухающие.
Были так же получены и определенны различные виды хаотических и не детерминированных движений системы:
а)
Гармонического осциллятора (![]()
![]() [0.479,0.536]
[0.479,0.536]
![]() [1.265,
2.159]).
[1.265,
2.159]).
б)
Субгармонический осциллятор (![]()
![]() [0.
355,0.423]
[0.
355,0.423]![]() [2.160,
2,847]
[2.160,
2,847]
![]() [3.5,
5.5]).
[3.5,
5.5]).
в)
Квазипериодический осциллятор (![]()
![]() [0.
588,0.595]
[0.
588,0.595]
![]() {0.
780}
{0.
780}![]() [2.848,
2.888]).
[2.848,
2.888]).
г) Хаотический осциллятор (Все остальное множество значений, подробно проанализированное по классам движений в нелинейных детерминированных системах в п. “ Обсуждение результатов ”).
