Представлення інформація в пам’яті пк
Основним об'єктом обробки в ПК є дані. Дані розрізняються типами, що пов'язано з різною їхньою природою (числа, символи, графічні зображення, звуки, тощо).
Для автоматизації роботи з різнотипними даними важливо уніфікувати їхню форму представлення. Для цього використовуються різноманітні прийоми кодування, зокрема, вираження даних одного типу через дані іншого типу.
Позиційні системи числення
В питаннях організації обробки інформації за допомогою ПК важливе місце займають системи числення.
Під системою числення розуміють спосіб представлення числа за допомогою обмеженої кількості цифр і літер та правила виконання арифметичних дій над цими числами.
Розрізняють позиційні та непозиційні системи числення. В непозиційнійсистемі числення число визначається тільки набором цифр (літер), які в нього входять (наприклад,римськасистема числення - ХХІ). Впозиційнійсистемі числення значення числа визначається як набором цифр (літер), так і їх позицією в числі. В інформатиці використовуються тільки позиційні системи числення.
Представлення числа в такій системі числення визначається формулою:
де q–основа системи числення;
X(q) – запис числа в системі числення з основою q;
хі – значення цифри на і-позиції (ціле число, менше за q);
i –розряд числа;
n – число розрядів (позицій) в цілій частині числа;
m – число розрядів в дробовій частині числа;
qі – вага цифри на і-позиції.
Наприклад: 4295, 6731(10) = 4 103 +2102+ 9101 +5100 +610-1 + 710-2+ 110-4.
Тип системи числення визначається її основою – кількістю символів (цифр та літер), що служать для представлення числа. Найбільш розповсюдженими в інформатиці, окрім десяткової і двійкової систем числення, є вісімкова та шістнадцяткова системи:
в вісімковій для представлення чисел використовується 8 цифр: 0,1 ... 7 (q = 8)
в шістнадцятковій алфавіт включає 16 символів: 0, 1 ... 9,А,В,С,D,Е,F(q = 16)
Співвідношення чисел в найбільш розповсюджених системах числення:
-
10
2
8
16
10
2
8
16
0
0
0
0
12
1100
14
С
1
1
1
1
13
1101
15
D
2
10
2
2
14
1110
16
E
3
11
3
3
15
1111
17
F
4
100
4
4
16
10000
20
10
5
101
5
5
17
10001
21
11
6
110
6
6
18
10010
22
12
7
111
7
7
19
10011
23
13
8
1000
10
8
20
10100
24
14
9
1001
11
9
21
10101
25
15
10
1010
12
A
22
10110
26
16
11
1011
13
В
...
...
...
...
Правила переведення чисел із однієї системи числення в іншу
Переведення чисел із десяткової системи числення в інші системи числення. Виконується за правилами ділення-множення: для переведення цілої частини числа використовується правило ділення; дробової - правило множення.
Правило ділення. Ціле десяткове число ділиться на основу тієї системи числення, в яку воно переводиться, доки частка не стане меншою за основу. Число в новій системі числення записується у вигляді останньої частки і всіх залишків від ділення, починаючи з останнього.
Наприклад,
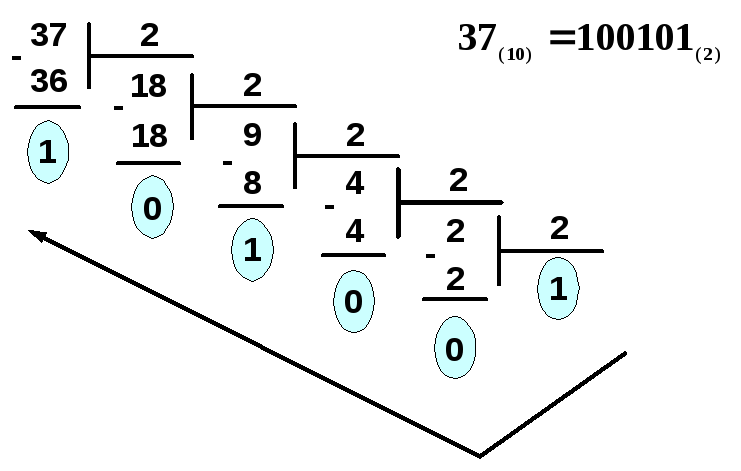
Правило множення. Дробова частина десяткового числа послідовно перемножується на основу тієї системи числення, в яку переводиться число. Число в новій системі числення записується у вигляді цілих частин отриманих добутків, починаючи з першої.
Наприклад,
Для перетворення змішаних чисел використовується обидва правила (відповідно для цілої та дробової частин числа).
Переведення чисел в десяткову систему числення. Виконується за правилом заміщення, що реалізується на основіформули представлення числа в позиційній системі числення:
100101 (2) = 125 + 024 + 023 + l22 + 021 + l20 = 32 + 4 + 1 = 37(10)
0,1l011 (2) = 12-1 + 12-2 + 02-3 + l2-4 + l2-5 = 0,5 + 0,25 + 0,0625 + 0,03125 = 0,85(10)
100101,1l011 (2) = 125 + 024 + 023 + l22 + 021 + l20 + 12-1 + 12-2+ 02-3 + l2-4 + l2-5 =
32 + 4 + 1 + 0,5 + 0,25 + 0,0625 + 0,03125 = 37,85(10)
Скорочені правила переведення чисел.
При переведенні двійкового числа в вісімкове воно ділиться на тріади (відносно коми), які замінюються вісімковими числами:
111 001 101,010 (2)= 715,2(8).
При переведенні двійкового числа в шістнадцяткове воно ділиться на тетради (відносно коми), які замінюються шістнадцятковими цифрами:
0001 1100 1101,0111(2)= 1CD,7(16).
При переведенні вісімкового числа в двійкове кожна його цифра замінюється двійковою тріадою:
715,2(8)= 111 001 101,010 0(2).
При переведенні шістнадцяткового числа в двійкове кожна його цифра замінюється двійковою тетрадою:
1CD,7(16) = 0001 1100 1101,0111(2).
Якщо при розбитті двійкового коду в крайніх тріадах (тетрадах) недостатньо цифр, вони доповнюються нулями. Відповідно, «зайві» нулі, що не ввійшли в тріади (тетради) відкидаються.