36

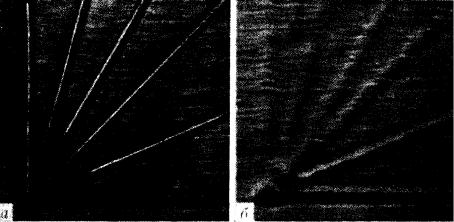
ориентирована параллельно им. Степень полноты залечивания убывает по мере перехода от первой к последней царапине (рис.25).

После того как мы поняли, что направленный поток атомов сопровождается движением ступеней (не макроскопических ступеней естественной шероховатости, а микроскопических атомных ступеней), легко понять, почему не все царапины веера залечиваются одинаково. От залечивающейся царапины должны разбегаться микроскопические атомные ступени. Не во всех направлениях им двигаться одинаково легко. Их путь пересекается ступенями естественной шероховатости. Атомные ступени, которые перемещаются в направлении, параллельном макроскопическим ступеням, испытывают наибольшее торможение. Видимо, в этом все дело.

Рис. 25. Веер царапин до (а) и после (б) отжига на поверхности кристалла золота, покрытой ориентированными ступенями «естественной шероховатости». Увеличение 300.

Канавки термического травлений

Явление, о котором я хочу рассказать, внешне выглядит диаметрально противоположным описанному в предыдущем очерке: при высокой температуре на полированной поверхности металлического образца происходит не сглаживание различных неровностей, а, наоборот, формируются канавки, которые сложным узором покрывают поверхность. Наблюдение следует уточнить: канавки располагаются на поверхности металлического образца не произвольно, а вдоль линий пересечения поверхности межзеренными границами. Очень удачный термин — «канавки». Они подобны земляным канавам, из которых землю выбрасывают на берега. По мере углубления канавок на поверхности металла на их берегах формируются выпуклости, объем которых в точности равен объему канавки.

Перед тем как приступить к обсуждению причины и механизма формирования канавок, утвердимся в мысли, что, хотя внешне явление как бы противоречит разумному Эффекту сглаживания поверхности, оно, как и упомянутый «разумный» эффект, должно сопровождаться уменьшением энергии. Если бы энергия в процессе формирования канавок самопроизвольно увеличилась, процесс не происходил бы. А он происходит. Следовательно, энергия понижается, «камень катится с горы».

Начнем с того, что в том месте, где межзеренная граница пересекает плоскую поверхность кристалла, гладкость, заданная ей полировкой, не должна и не может сохраниться. Мысленно рассечем поликристалл плоскостью, перпендикулярной к полированной поверхности, и рассмотрим точку пересечения поверхности границей в плоскости сечения. Очевидно, что в этой точке О крыловская ситуация «лебедь, рак и щука» не реализуется, так как силы поверхностного натяжения свободных поверхностей лежат в одной плоскости, а сила, обусловленная наличием границы, направлена перпендикулярно к этой плоскости. Или во всяком случае имеет перпендикулярную составляющую, если граница наклонена по отношению к свободной поверхности. Под влиянием этой некомпенсированной силы точка О должна опускаться до тех пор, пока не установится такая геометрия канавки, при которой все силы, приложенные к точке О, уравновесятся. Глядя на рис. 26, легко убедиться, что угол при вершине канавки определяется уравнением

cosϕ =α12 / 2α .

37

Итак, появление канавки оправдано условиями равновесия в точке О. Его следует оправдать и энергетически — надо найти тот выигрыш в энергии, который делает формирование канавки разумным. Источник возможного выигрыша явно есть: при формировании канавки исчезает часть межзеренной границы. С ней связана граничная энергия которая, следовательно, выделяется. Это явно выгодно. Есть, однако, и обстоятельство, обусловливающее проигрыш энергии. Оно заключается в том, что по мере углубления канавки увеличивается площадь ее берегов, а с ней и величина поверхностной энергии. Очень непростым расчетом можно было бы показать, что выигрыш немногим превосходит проигрыш. Мы не станем прослеживать этот расчет, а убедимся, что дело обстоит именно так, на следующем простом и, по-моему, доказательном примере.

Рис. 26. Схема сил, уравновешивающихся в вершине канавки термического травления.

Обсудим судьбу тонкой бесконечной пластины, состоящей всего из двух зерен, разделенных границей, которая расположена перпендикулярно обеим поверхностям пластинки. В процессе длительного отжига канавки будут формироваться с обеих сторон, двигаясь одна навстречу другой. Береговые холмы будут расти. Процесс завершится тогда, когда канавки встретятся, и пластина распадется на две. На торце каждой из них перед распадом формируется утолщение — бывшие берега канавок. Процесс завершится очевидно выигрышем энергии: межзеренная граница исчезнет, а энергия, связанная с цилиндрической кромкой, подбором радиуса цилиндра всегда может быть сделана такой, чтобы прирост энергии вследствие оголения торцов при распаде был заведомо скомпенсирован энергией, которая выделилась при исчезновении межзеренной границы.

Нам осталось обсудить вопрос о механизме формирования канавки. На начальном этапе, когда канавка еще мала, основным оказывается механизм поверхностной диффузии: из области вершины канавки атомы по поверхности диффундируют к ее берегам. Ограничимся именно этим этапом процесса.

Рис. 27. Последовательность интерферометрических снимков, полученных от поверхности развивающейся канавки термического травления. Увеличение 500.

Без особого труда можно выяснить закон, которому подчиняется изменение глубины (h) или ширины (l) канавки со временем. Изменяясь, канавка остается почти себе подобной,— то подтверждается экспериментом (рис. 27); поскольку h l ,то площадь сечения канавки

S h2 l 2 . Очевидно, эта площадь, образовавшаяся за время t вследствие ухода атомов из

38

вершины канавки к ее берегам, будет пропорциональна коэффициенту поверхностной диффузии DS , времени t и силе, определяющей поток. При данных значениях величин α12 и

αона, очевидно, обратно пропорциональна расстоянию от точки О до берега, т е. величине

~1 12 , и обратно пропорциональна тому пути, который атому надлежит проделать, т. е.S

из которого следует, что

S2 ~ DSt или l ~ h ~ (DSt)1/4.

Этот закон экспериментально подтверждается настолько точно, что данные о временной зависимости h и l широко используются для надежного определения коэффициента поверхностной диффузии. Это очень ценная возможность, так как коэффициент поверхностной самодиффузии при этом определяется без использования радиоактивных изотопов.

«Кристаллу не пристало терять черты кристалла»

У поэта Сергея Смирнова есть стихотворение, в котором точно передано одно из самых важных свойств кристалла.

Вот оно:

Не в ту среду попал кристалл, Но растворяться в ней не стал:

Кристаллу не пристало Терять черты кристалла.

Кристалл как бы борется за «право первородства», за сохранение своих черт в виде отчетливой огранки совершенной формы.

В кристалле, которому искусственно придана форма, отличная от естественной, равновесной, будут происходить процессы, ведущие к восстановлению равновесной формы. Причина этого обсуждалась уже несколько раз: камень, поднятый на гору, при первой же возможности скатится к ее подножию. Направленный перенос вещества, необходимый для формирования равновесной огранки, или, как говорят кристаллографы, равновесного габитуса, одновременно будет происходить всеми возможными способами или механизмами: диффузией через газовую фазу, диффузией в объеме, диффузией по поверхности. В этой конкуренции механизмов главенствовать будет тот, который с наибольшей скоростью осуществляет преобразование формы кристалла в равновесную. Количество вещества, перенесенное механизмом объемной диффузии через газовую фазу, пропорционально квадрату размера кристалла, так как с изменением размера кристалла изменяется площадь «фронта», через которую переносится вещество. Если размер кристалла l, то площадь этого «фронта» ~l2. A площадь «фронта» поверхностной диффузии в таком кристалле будет ~lδ, где величина б характеризует толщину слоя, в котором происходит поверхностная диффузия, и равна эта величина приблизительно межатомному расстоянию. Таким образом, очевидно, что с уменьшением размера кристалла относительная роль поверхностной диффузии будет увеличиваться и для очень маленьких кристалликов она будет определяющей при температурах, близких к температуре плавления. Оказывается, что кристаллики из золота, меди, платины, серебра, если их размер меньше 10 мк, будут «бороться» за свои черты с помощью механизма поверхностной диффузии.

39

Рис. 28. Микроскопические крупинки золота, сфотографированные в электронном микроскопе.

Великолепные фотографии микрокристалликов золота были получены исследователями с помощью электронного микроскопа. После напыления атомов золота на подложку атомы, сгруппировавшись, образовали крупинки неправильной формы. После отжига при высокой температуре эти крупинки обретали форму ограненных кристалликов. На рис. 28 приведены фотографии трех различно ориентированных ограненных крупинок золота. По времени, в течение которого бесформенная крупинка обретает огранку, можно оценить коэффициент поверхностной диффузии. Мы этого делать не станем, но если бы сделали, то убедились бы, что именно поверхностная диффузия восстановила черты кристалла золота, который изображен на приводимой фотографии.

А вот другой опыт, свидетельствующий все о том же. В этом опыте изучалось поведение не кристаллика, а «отрицательного полукристаллика», т. е. искусственно созданного на поверхности ограненного углубления. Опыт ставился так. На поверхности естественного скола монокристалла каменной соли вдавливанием четырехугольной пирамидки создавались два углубления. Во всем они были одинаковы, отличались только ориентацией. След одного укола был ориентирован так, что очерчивающие его линии были параллельны граням кристалла, а другой по отношению к ним был повернут на 45°. После длительного отжига оказалось, что первый след укола существенно уменьшился, не изменив при этом ориентации, а второй и уменьшился, и, переориентировавшись, расположился параллельно первому. В процессе переориентации существенную роль играла поверхностная диффузия

— в этом убеждают специальные контрольные опыты.

Уменьшение объема уколов мы обсуждать не станем. Ясно, что оно происходит именно потому, что при этом поверхность уменьшается. А вот поворот — это уже борьба за «черты кристалла». Первый укол ориентирован более благоприятно, а второй поворачивается, и оба следа, имевшие вначале острую вершину, становятся плоскодонными. Принудительно созданное и неблагоприятно ориентированное углубление в кристалле в конце концов ограняет себя поверхностями, параллельными естественным граням кристалла. Сказанное иллюстрирует рис. 29.