124

ках, точнее, в разобщенных маленьких островках. Такая крупинка под влиянием случайных толчков будет легко смещаться, подчиняясь законам хаотической броуновской миграции. Происхождение толчков может быть самым различным. В частности, они могут быть обусловлены флуктуационными перемещениями атомов соли под крупинкой или флуктуационным смещением части атомов в крупинке в одном направлении, вследствие чего вся крупинка получит толчок в противоположном.

По той или иной причине крупинки будут неупорядоченно мигрировать по поверхности и, следовательно, диффузионно смещаться в ту часть кристалла, где их прежде не было. В каждом последовательном скачке крупинка может изменить положение центра своей тяжести, но и немного повернуться, улучшив контакт с подложкой. Это стремление к укреплению силовой связи оправдано, так как при этом уменьшается поверхностная энергия границы раздела крупинка — соль. Очевидно, должен наступить момент, когда сила неупорядоченно действующих толчков окажется недостаточной для того, чтобы сместить крупинку, прочно связанную с солью. Это и будет означать, что «запас бодрости» крупинки исчерпан, ее участие в диффузионной миграции исключено.

Итак, Керн наблюдал физически совершенно оправданный эффект. При первом знакомстве он настораживает. Это, однако, объясняется не столько существом эффекта, сколько манерой нашего мышления: неожиданное всегда настораживает.

Вынужденное движение крупинок по поверхности кристаллов

О невынужденном движении металлических крупинок по поверхности ионного кристалла было рассказано в очерке об опытах профессора Керна. В этих опытах самопроизвольное метание крупинок завершалось их успокоением. После множества скачков-попыток они располагались так, чтобы лучшим образом приспособиться к структуре кристалла соли. Случайно возникающих сил становилось явно недостаточно для смещения удобно устроившейся крупинки.

Естественно предположить, что крупинка на поверхности, как и крупинка в объеме кристалла, должна направленно перемещаться под влиянием силы, приложенной к ней. Так же как и в объеме, движение крупинки на поверхности, видимо, должно происходить тем быстрее, чем выше температура. Попросту говоря, под влиянием силы крупинка должна не самопроизвольно, а вынужденно двигаться в направлении, которое указывается силой.

Ничего интересного нельзя было бы рассказать об этом движении, если бы сила была настолько большой, что могла бы попросту сорвать крупинку и как целое увлечь за собой. Разве лишь интересно было бы определить наименьшее значение силы, достаточное для того, чтобы сорвать крупинку с места, но рассказывать об этом в книге о диффузии вряд ли бы стоило. Для нас, интересующихся диффузией, надо разобраться в судьбе крупинки, на которую действует такая сила, которая недостаточна для того, чтобы сорвать крупинку с местa, но вполне достаточная для ее диффузионного перемещения.

Чтобы уяснить себе диффузионный механизм движения крупинки по поверхности, обсудим ее судьбу при двух различных положениях на кристалле. Будем предполагать, что в одном из положений крупинка подобна лепешечке на гладкой поверхности кристалла, или, лучше, капле воды на поверхности стекла. В другом положении крупинка как бы вдавливается в тело кристалла, на котором находится. Такое вдавливание вполне оправдано стремлением крупинки приобрести форму, при которой связанная с ней поверхностная энергия будет минимальной. Какое из двух возможных положений осуществляется в действительности, зависит от очень многих обстоятельств, а главным образом от того, из каких веществ изготовлены крупинка и кристалл, при какой температуре они находятся в контакте и как давно контакт установился. Чтобы разобраться в интересующем нас вопросе, надо обсудить и один, и другой случай.

Вначале о крупинке-лепешке. Продолжим аналогию с каплей воды на поверхности стекла. Если к капле приложить силу, например наклонив стекло, капля начнет по стеклу двигаться, не скользя, а как бы переливаясь, перенося часть жидкости из тыльной части в лобовую. Говоря о жидкой капле, мы нашли подходящее слово: она переливается. А в

125

кристаллической крупинке под влиянием внешней силы вещество будет диффузионно переноситься от лобовой к тыльной части.

Схематически все очень похоже на то, что рассказывалось о движении крупинок в объеме. В действительности, однако, в поверхностном варианте движения есть очень существенные отличия. Во-первых, при диффузионном механизме движения, когда крупинка движется не как целое, а вследствие поатомного переноса массы в ее лобовую часть, движение начнется лишь после того, когда будет преодолена некоторая сила трения. Реальность этой силы легко представить себе, вспомнив, что капелька воды, перетекая, поползет по стеклу лишь после того, когда стекло будет наклонено под углом, большим некоторого предельного; когда составляющая силы тяжести вдоль плоскости стекла станет больше силы, препятствующей перетеканию. Эта сила и имеет смысл силы трения. Возникает она в связи с тем, что для отрыва жидкости от стекла в тыльной части капли надо затратить энергию. До отрыва удельная энергия, связанная с границей жидкость — твердое, равнялась . После отрыва жидкости от твердого тела образуются две поверхности, одна из них — свободная поверхность жидкости с энергией , а вторая — свободная поверхность твердого тела с энергией . Таким образом, интересующая нас энергия отрыва в расчете на 1 см2 равна . Имея в виду каплю, которая с поверхностью твердого тела соприкасается по кругу диаметром , величину силы трения можно вычислить, следуя очевидной логике. Мысленно сместим каплю как целое на некоторое расстояние х. При этом будет выполнена определенная работа, равная произведению площади, на которой оголилось твердое тело, на величину . Легко сообразить, что эта площадь равна , и, следовательно, выполненная работа . А так как работа равна произведению силы на путь , то .

У читателя может возникнуть вопрос: почему учитывается затрата энергии на отрыв тыльной части капли от поверхности твердого тела и не учитывается выигрыш энергии вследствие «набегания» лобовой части капли на эту поверхность? Он появляется в связи с тем, что переливающаяся капля закроет собой часть твердой поверхности, у которой велика удельная поверхностная энергия. Выигрыш энергии вследствие «набегания» лобовой части в точности равен проигрышу вследствие отрыва тыльной части. Дело в том, что энергия, выигранная при «набегании», не используется для облегчения отрыва. Она просто рассеивается и немного нагревает каплю. Здесь ситуация подобна той, в которую попадает идущий по болоту: левую ногу не легче вытаскивать из трясины от того, что правая легко тонет в трясине. Кстати заметим, что идущий по болоту нагревается! Очень! Итак, диффузионное движение частицы начнется лишь после того, как приложенная сила превзойдетсилу трения.

Вторая особенность движения крупинки-лепешки по поверхности заключается в том, что, как показывают расчеты, наиболее эффективный перенос массы осуществляется вследствие диффузии вдоль границы раздела крупинка—кристалл. Приграничный слой оказывается как бы в роли смазки, по которой лепешка может легко скользить как целое.

Теперь о случае, когда крупинка немного вдавливается в тело кристалла. Если ее движение происходит до занными с ней. Эта связь обусловлена тем, что смещение границы под крупинкой от зерна 1 к зерну 2 может привести к увеличению граничной энергии, если ее величина на границе крупинка — зерно 1 больше, чем на границе крупинка — зерно 2. Благодаря этой связи движущаяся граница может увлекать за собой крупинки. Именно это в описываемом опыте и наблюдалось. Наблюдалась еще одна любопытная особенность процесса. Межзеренная граница, пересекающая поверхность образца, в процессе рекристаллизации движется скачкообразно. Об этом ранее было рассказано в специальном очерке. Оказывается, вначале скачка сила, с которой граница действует на крупинку, превосходит силу связи с ними; граница отрывается от крупинок, оставляя их за собой, а затем где-то перед очередной остановкой, когда связь между границей и крупинкой сохраняется, граница их увлекает за собой. В этом многократно повторяющемся процессе на поверхности кристалла образуется полосчатая структура, в которой зоны, свободные от крупинок, чередуются с зонами, где крупинок много.

126

Результаты одного и другого опыта могут быть использованы для вычисления коэффициентов диффузии, которые определяют перенос массы, необходимой для движения крупинок. Этим вычислениям место в специальных статьях и книгах, а здесь удовлетворимся качественной иллюстрацией того, что под влиянием силы крупинки могут вынужденно перемещаться по поверхности кристалла.

127

Коалесценция в режиме «подметания»

С движением крупинок по поверхности кристалла, увлекаемых границей или подталкиваемых ступенькой, мы уже встречались: крупинка перемещается как целое, диффузионно скользя по поверхности. Далее для определенности я все время буду иметь в виду ступеньки, движущиеся вдоль поверхности. Именно для определенности, так как все рассказанное о движущейся ступеньке может иметь прямое отношение и к движущимся в объеме дислокации или межзеренной границе.

Если крупинка на поверхности не одинока, а принадлежит ансамблю ей подобных, перед движущейся ступенькой будут накапливаться крупинки, ступенька их статочно медленно для того, чтобы под крупинкой формировалась ямка, движущаяся вследствие диффузионного переноса массы в объеме кристалла, закономерности и механизм движения такой крупинки оказываются совершенно подобны движению крупинки в объеме. Вместе с ямкой перемещается та часть крупинки, которая внедрена в кристалл, и при этом как бы везет на себе ту часть, которая находится над поверхностью.

Расскажу о двух опытах, в которых наблюдалось диффузионное движение крупинок вдоль поверхности. Они отличаются и объектами исследования, и происхождением силы, приложенной к крупинкам.

В одном из опытов изучался процесс конденсации пара каменной соли на монокристалл каменной соли в условиях, когда на поверхности монокристалла было расположено большое количество крупинок золота. Их размер не превосходил десятой доли микрона. Известно, что в процессе конденсации новые слои наращиваются вследствие движения ступеней, которыми богата любая поверхность кристалла. Встречая на своем пути крупинки, ступени толкают их. Сила, действие которой испытывают на себе крупинки, зависит от многих величин: высоты ступени, расстояния между крупинками вдоль ступени, интенсивности того потока пара, который падает на поверхность кристалла.

О том, что частицы золота, подгоняемые ступеньками, действительно движутся, можно судить по электронно-микроскопическим снимкам, на которых видно, что за движущимися ступенями крупинок золота нет, а перед ними крупинок много. Некоторые из них, столкнувшись, образовали большие крупинки, каких раньше на поверхности не было. Этот эффект особенно впечатляет, когда движущаяся ступень имеет форму замкнутой кривой, контуры которой движутся от центра. В этом случае на поверхности кристалла формируются участки, внутри которых крупинок нет, а их контуры обрамлены крупными слившимися крупинками.

Второй опыт был осуществлен с образцами поликристаллической меди, на поверхности которой были хаотически расположенные крупинки окислов. Межзеренные границы, пересекающие поверхность образца, в процессе рекристаллизации движутся. Те из крупинок, которые попадают на движущуюся границу, могут оказаться свя будет как бы подметать, подобно венику, подметающему мусор. Новые крупинки, увлекаемые ступенькой, будут осаждаться либо на ступеньке, либо на тех крупинках, которые уже со ступенькой движутся. Сталкивающиеся крупинки могут диффузионно сливаться воедино. Этот процесс слияния и является коалесценцией в режиме «подметания». Он обнаружен недавно, но, видимо, привлечет к себе внимание и физиков, и инженеров.

Коалесценции в режиме «подметания» свойственны две характерные скорости: скорость диффузионного слияния столкнувшихся крупинок и скорость движения «подметающей» ступеньки . Величину оценить не сложно, после того как на стр. 105 мы получили оценку — времени, необходимого для слияния. Очевидно,

и если крупинки достаточно малы для того, чтобы их слияние определялось поверхностной диффузией, то

Если см, а при высокой температуре см2/сек и эрг, то скорость слиянияможет оказаться большой; см/сек. Очевидно, что для того чтобы такой процесс имел место, необходимо, чтобы ступенька двигалась со скоростью, значительно меньшей скорости слияния. В ином случае крупинки,

128

накапливающиеся перед фронтом подметающей ступеньки, не будут успевать диффузионно сливаться, будут сохранять свою обособленность. Этот «недиффузионный» случай неинтересен. О нем мы говорить не будем.

Обсудим вначале коалесценцию в режиме «подметания» схематически, а затем, сопоставив схематическую картину с результатом эксперимента, увидим, насколько реальная ситуация богаче и сложнее вполне разумной схемы.

Итак, схема: прямолинейная ступенька движется вдоль поверхности, на единичной площади которой хаотически расположено одинаковых крупинок, имеющих радиус . Двигаясь и «подметая» крупинки, ступень остается прямолинейной. Как уже упоминалось, те крупинки, к которым подошла ступень, могут осесть либо на ней, либо на уже осевших крупинках.

Схематическая картина процесса и иллюстрируется, и подтверждается столь же схематически поставленным экспериментом: одинаковые черные кружочки расположены на белом листе, параллельно себе перемещается линейка и «подметает» их; два столкнувшихся кружочка заме няются третьим, радиус которого соответствует крупинке, имеющий суммарный объем столкнувшихся крупинок (рис. 85).

Рис. 85. Последовательность этапов модельного опыта по коалесцен-ции в режиме «подметания».

Теперь о реальном эксперименте. Наблюдение велось за судьбой крупинок золота на поверхности монокристалла NaCl в условиях, когда на ней конденсируются пары NaCl и, следовательно, ступени, поглощая молекулы соли, движутся. Поток пара NaCl подбирается так, чтобы выполнялось условие: . Коалесценция «подметаемых» крупинок действительно происходит: за движущейся ступенью возникает зона, свободная от крупинок, перед ступенью — укрупненные частицы золота. Существенная особенность реального процесса заключается в том, что движущаяся ступень в отличие от линейки в схематическом модельном опыте прогибается между соседними крупинками. Этот прогиб имеет любопытное следствие: те крупинки, которые ступень встречает ниспадающими участками своего контура, как бы скатываются по ним к крупинкам в местах закрепления ступени. Это скатывание, как и движение, может осуществляться с помощью диффузионного механизма: объемного или поверхностного. Скатывание приводит к тому, что укрупнение частиц на ступени происходит существенно быстрее, чем можно ожидать на основании модельного эксперимента с жесткой линейкой.

Рис. 86. Коалесценция в режиме «подметания» крупинок золота на поверхности монокристалла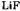. Увеличение 15 000.