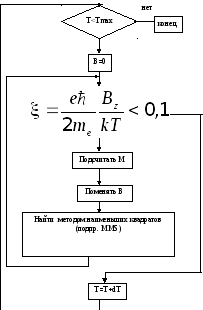
Алгоритм

Тестовый пример: Т=300; 0,1<В<1,

Построить график зависимости намагниченности системы от индукции внешнего поля.

Задание: получить экспериментально закон Кюри, т. е. обратную пропорциональность между магнитной восприимчивостью и абсолютной температурой.

Для этого воспользоваться вспомогательным алгоритмом:

Практичне заняття 12.

.

Модель ферромагнетика.

Физические свойства ферромагнетиков - краткие сведения

1. - магнитная проницаемость для ферромагнетиков не является постоянной, она зависит от внешнего магнитного поля немонотонно и может достигать порядка 10⁴. В сильных полях благодаря насыщению намагниченности величина  стремится к 1. 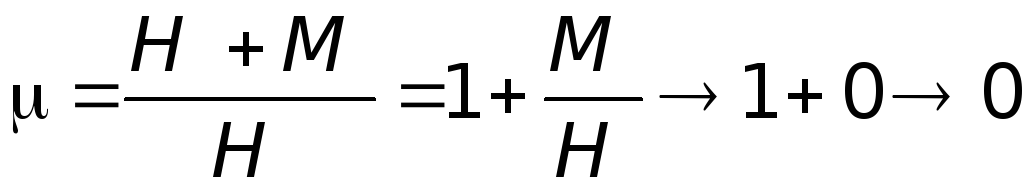(посмотрите формулу в предыдущей лекции).- намагниченность; Н- напряженность магнитного поля.

2. Существует остаточная намагниченность, приводящая к появлению гистерезиса.

3. Существует спонтанная намагниченность - даже не намагниченный в целом образец состоит из областей спонтанной намагниченности - доменов.

Границы между областями называют доменными стенками.

Ферромагнитные свойства являться результатом взаимодействия между магнитными моментами, которое имеет чисто квантовую природу (обменное взаимодействие). При высоких температурах это взаимодействие не играет существенной роли, и вещество имеет чисто парамагнитные свойства.

Модель для компьютерного эксперимента (метод МК).

Задача компьютерного эксперимента состоит в том, чтобы:

1. Проиллюстрировать явление магнитного упорядочивания.

2. Получить и исследовать явление гистерезиса.

Рассмотрим 2-х мерную кристаллическую решетку, в узлах которой находятся атомы с магнитными моментами . Тогда каждый атом решетки описывается двумя координатами (i, j) и характеризуется переменной _ij, которая может принимать только два значения: +1 и -1, т.е. направления элементарного магнитного момента. В этом случае энергия взаимодействия двух соседних атомов будет выражаться зависимостью:

, где

1. обменный интеграл.

Каждый атом имеет 4-х ближайших соседей, т.е. вклад в его энергию внесут 4 ближайших атома. Тогда энергия взаимодействия для атома ( i,j), магнитный момент которого направлен , можно вычислить по формуле:

Возьмем для моделирования достаточно небольшую область пространства: 100100 магнитных моментов. При этом возникает проблема выбора граничных условий. Используя граничные условия Борна- Кармана, согласно которым для области из nm моментов вместо столбца с координатой i=0 берётся столбец i=n, а вместо ряда с координатой j=0 берётся ряд атомов с координатой j=m. Аналогично _n+1,j=_1,j и _i,m+1=_i,1. Этим обеспечивается равноправие всех атомов. Выражение для полной энергии, приходящейся на 1 магнитный момент в узле i,j:

.

Вероятность конкретного состояния:

Реализация микросостояний системы производиться методом Монте- Карло последовательно для каждого атома. Поскольку атомы перебираются последовательно, от первого до последнего, легко определить, что вероятность конкретного состояния для каждого из них будет подсчитываться на основе двух "новых" состояний атомов из двух "старых" состояний других двух атомов. Чтобы устранить этот недостаток, ориентацию магнитного момента атома будем определять в два этапа. На первом- проводим переопределение состояний каждого атома, от первого до последнего, а на втором- наоборот, от последнего до первого. Дальнейшая процедура ничем не отличается от описанной в предыдущем алгоритме. Можно исследовать явление остаточной намагниченности и получить петлю гистерезиса. Для этого нужно исследовать изменение намагниченности системы с увеличением индукции внешнего поля , выбравI достаточно большим, чтобы обеспечить ферромагнитное состояние системы (Т ниже Т_Кюри).

Тестовый пример: В_мах=300, Т=60, I=1е-21.

Алгоритм

Модель перехода пара- ферромагнетик (Гусок, 2.13.-на самостоятельную работу).

Решение уравнения диффузии.

Постановка задачи (одномерный случай)

На пластине шириной l на левой границе размещен точечный источник с постоянной концентрацией с, на правой границе поток =0.

Численно решается уравнение диффузии

; D-коэффициент диффузии.

В алгоритме используеться метод конечных разностей для решения уравнений в частных производных, в котором частные производные заменяют конечными разностями по формулам:

Тогда уравнение диффузии имеет вид:

Шаг по времени dt и по координате dх связаны соотношением (для сходимости метода). Число (количество) точек по координате.

Значения концентрации известны в дискретных точках, в дискретные моменты времени и определяются через соответствующие концентрации в предыдущий момент времени. В дискретных точках значения концентраций описывают через массив C_old, Cnew с индексами n в моменты времени t-dt, t.

Алгоритм