Алгоритм 1

Тестовый пример:

M=1000; N=100; h=2.

Задание:

1. Выполнить алгоритм с учетом "ветра" (разная вероятность шагов вправо- влево и проверить параболический закон.

2. Модифицировать алгоритм для двухмерного случая (шаги вправо- влево, вверх- вниз) и подсчитать средний квадрат смещения, как x²+y². Вывести на экран частицу.

Генераторы случайных чисел.

Обратим внимание на 1 пункт алгоритма.

Для его реализации необходимы случайные числа.

Способы решения задач, которые используют случайные числа, называют стохастическими методами, или методами Монте-Карло. Простейшим генератором случайных чисел была рулетка.

Однако из-за трудоемкости моделирования случайных чисел, только с появлением ЭВМ метод приобрел широкое распространение. Считают, что он появился в 1949 году, а его авторы-американцы Дж. Нейман и С. Улам.

Насколько хороши методы МК из-за их стохастической природы зависит от качества генератора случайных чисел. Генератор должен иметь такие свойства:

1. Хорошие стохастические свойства

2. Эффективность

3. Большой период

4. Воспроизводимость

I- й пункт- наиболее важен. На самом деле генерируют не случайные числа, а последовательность псевдослучайных чисел. Все генераторы создают такие последовательности с помощью рекуррентных соотношений, используя функцию остатка. Такая последовательность через период повторяет себя, так, что период должен включать хотя бы необходимое для эксперимента множество случайных чисел. Эффективность генератора важна, т. к. требуется большое количество случайных чисел (10¹⁰) + экономия памяти.

Воспроизводимость - нужна, чтобы проверить влияние на результаты моделирования случайных чисел изменений в алгоритме. Примером алгоритма получения псевдослучайных чисел может служить предложенный Дж. Нейманом метод середины квадратов. Четырехзначное число возводится в квадрат, четыре внутренние цифрыопять в квадрат, и т. д. Случайными принимаются 4- х значные числа,. Этот метод дает непропорционально много малых значений.

Наиболее популярны сейчас линейные конгруэнтные генераторы.

где, ,

Внедренная продуктивность и возможность свести значения до отрезка (делением наmax). При -смешанный генератор (max период), при -мультипликативный.

Практичне заняття 2.

Случайные блуждания и распределение вероятностей.

Мы помним, что микросостояние системы большого количества частиц нестойки даже при малых флуктуациях. Это значит, что предвидеть состояние макросистемы невозможно в принципе. Микрособытия в макросистеме являются истинно- случайными. Главное задание статистической физики - находить вероятности состояний и микрособытий.

На прошлом занятии мы рассмотрели алгоритм, позволяющей смоделировать случайные блуждания (одномерный случай) ансамбля из М частиц (независимых друг от друга), и оценить, как выполняется параболический закон диффузии (средний квадрат смещения частицы пропорционален времени случайных блужданий). В этой задаче мы вычисляем средний квадрат смещения, усредненный по ансамблю.

Сегодня мы рассмотрим подобный алгоритм, (и подобную модель), но поставим задачу получить на выходе программы распределение вероятностей положения частиц при случайных одномерных блужданиях.

Постановка задачи: Пусть частица может двигаться вправо с вероятностью р, а влево- с вероятностью q=1-p с одинаковым шагом h. Необходимо определить, с какой вероятностью P_N(x) через N шагов частица будет находиться на расстоянии N от начальной точки x₀=0.

Очевидно, что тут можно было бы использовать компьютер как генератор всех возможных перестановок блужданий. Например, если рассмотреть 3 шага случайных блужданий, то 8 возможных траекторий выглядит следующим образом:

  ;   ;   ;

  ;   ;   ;

Т. е. у нас возможны два варианта со смещением на 3 шага (вправо с вероятностью р³ или влево с вероятностью q³) и 6 вариантов смещения на 1 шаг (3 вправо с вероятностью p²q или три влево с вероятностью pq²). Тогда среднее смещение

Количество возможных траекторий блужданий в одномерном случае 2^N (для нашего рассмотренного случая- 8), то для d- мерного пространства подсчет количество блужданий ограничен из- за громоздкости операций.

X Альтернативным вариантом может быть выборка, статистический характер которой даст нам информацию про процесс в целом. Если рассмотреть ансамбль частиц, каждая из которых независимо от других проходит случайный путь длинной N шагов из начальной точки, то большинство частиц после одинакового количества шагов будут иметь одинаковую координату X_N. То есть, для определения вероятности нахождения частицы в точке X моделируется много ее запусков (М), по которым проводиться усреднение для определения среднего смещения на N шагов и определяется вероятность появления частицы в заданной точке X как:

где m- число запусков со смещением X.

В результате мы получили (графически) распределение вероятности в виде:

P_N(x)

X

Статистический характер задачи состоит в том, что мы рассматриваем либо большое количество случайных блужданий, либо большое количество одинаковых частиц, которые движутся одновременно.

Задача: показать, что, продолжив эти распределения, можно получить второй закон Фика (1855) - уравнение диффузии - говорящее о том, что случайные блуждания частиц приводят к перераспределению их концентрации согласно указанному закону.

Запишем алгоритм построения графика распределения вероятностей при случайных одномерных блужданиях - гистограммы P_K(m) с шириной столбца . М- число частиц, положение которых послеN шагов отвечает условию:

Для построения гистограммы нужно описать массив P с индексом от - К до К, где

; (Nh - максимально возможное смещение, когда все шаги однонаправлены), элементы которого будут отвечать числу частиц, попавших в данный интервал x.

Алгоритм 2

Тестовый пример: М=1000, N=100, h=2, X=5.

Примечание 1: начало координат 320, 440, масштабный множитель= 2, т. е. Координаты дополнительных узлов столбца:

(320+k2 xx 440);

(320+k2x+x 440+2pk)

Задание: Проверить, что полученное распределение - является распределением Гаусса. Использовать метод наименьших квадратов для значений ((kx)², ln(pk)) для нулевых значений массива P, т. к. для распределения Гаусса

.

Чтобы завершить нашу "экскурсию в область диффузии", рассмотрим алгоритм модели, который реализовывает вакансионный механизм диффузии между атомами разного сорта методом МК.

Мы будем использовать модель плоской квадратной решетки, каждому узлу которой отвечает элемент массива а. Ячейки массива (узлы) имеют признаки, по которым определяется сорт атома и вакансий (например, целые числа, которые можно использовать, как цвет выведения ячеек на экран). Вначале примем, что правая половина решетки занята атомами сорта А. (зеленые, значения 2), левая - атомами сорта В (голубые-3). Вакансию разместим в одном узле решетки, для определенности выберем верхний левый угол (значение элемента массива-8). Бесконечность решетки nn обеспечим граничными условиями Борна-Кармана. На каждом шагу методом МК случайно выбираем направление прыжка вакансии длиной h в одном из четырех возможных направлениях и меняем местами вакансию и выбранный атом. Зададимся числом прыжков М.

Алгоритм 3 см. следующую страницу

Поменять местами вакансию и атом с координатами ivnew,jvnew

aiv, jv=aivnew, jvnew

aivnew, jvnew=8

Тестовый пример: n=30; M=104.

 Не забыть: попросить сделать алгоритм- задание с прошлого раза.

 предложить оформить протокол 1- ой лабораторной работы:

Моделирование диффузионных процессов методом МК на основе модели случайных блужданий.

Теоретические сведения

Алгоритмы (3 шт. + заданный в прошлый раз)

Распечатки кода

Результаты расчета; приложение - подпрограммы по бригадам.

Алгоритм 3

Практичне заняття 4.

Метод молекулярной динамики.

Основные параметры: состояние и ансамбли.

В основе моделирования лежит хорошо определенная модель физической системы, в расчете характеристики которой мы заинтересованы. Эти характеристики получают как средние по пространству состояний системы. Обозначим состояние системы как x=(x₁,…x_n), где n- число степеней свободы. Множество состояний системы составляет доступное ей фазовое пространство .

Систему можно описать, задавая ее микроскопическое состояние, (микросостояние). Такое описание дает нам наиболее полную, соответствующую законам механики характеристику каждой частицы системы.

В большем масштабе макроскопическое состояние (микросостояние) системы можно описать с помощью средних концентраций, температуры, объема и т. д.

В отличие от непредсказуемого микросостояния системы, макро состояние системы через некоторое время перестает меняться. Такое состояние называют равновесным.

Если макро состояние изолированной системы характеризуется величинами N- число частиц, V- объемом и Е- энергией, то на микроскопическом уровне в общем случае существует огромное количество способов- конфигураций- в которых может реализоваться данное макро состояние (N, V, E).

Конкретное микросостояние (конфигурация) есть достижимой, если его характеристики соответствуют данному макро состоянию. У нас нет причин отдать приоритет тому или другому состоянию; и можно утверждать, что в любой момент система равномерно находиться в одном из своих достижимых микросостояний (постулат ровных априорных вероятностей).

Если изолированная система имеет  достижимых равномерных состояний, то вероятность найти ее в микросостоянии S составляет:

P_S=

С точки зрения усреднения по времени, физический смысл вероятности P_S- доля времени, в течение которого одна система находится в микросостоянии S относительно всего времени наблюдения.

Ансамбль, который характеризуется величинами N, V, E и описывается распределением равных априорных вероятностей называют микроканоническим.

В реальных (лабораторных) условиях система не замкнута, а находиться в тепловом контакте с окружающей средой (формально- с тепловым резервуаром). Поскольку нас интересуют равновесные значения физических величин, то нужно знать вероятность P_l, с которой система находиться в состоянии S с энергией E_l. ансамбль, который характеризуется постоянными величинами N, V, T и описывается каноническим распределением Гиббса:

называется каноническим.

Тут z- статистическая сумма.

Задача про гармонический осциллятор.

Метод молекулярной динамики (М Д) вычисляет характеристики системы, используя уравнения движения. На ПК мы численно решаем уравнения движения, и для этого аппроксимируем их подходящей численной схемой, удобной для расчетов на ПК.

Определение:

Метод МД рассчитывает в фазовом пространстве траектории совокупности молекул, каждая из которых подчиняется классическим уравнениям движения.

Элементарный пример- задача про колебания тела, движущегося под действием упругой силы- одномерный гармонический осциллятор.

Мы задаем гамильтониан, который описывает движение тела под действием упругой силы с k - коэффициентом упругости:

;

далее, используя законы классической механики и разложение в ряд Тейлора:

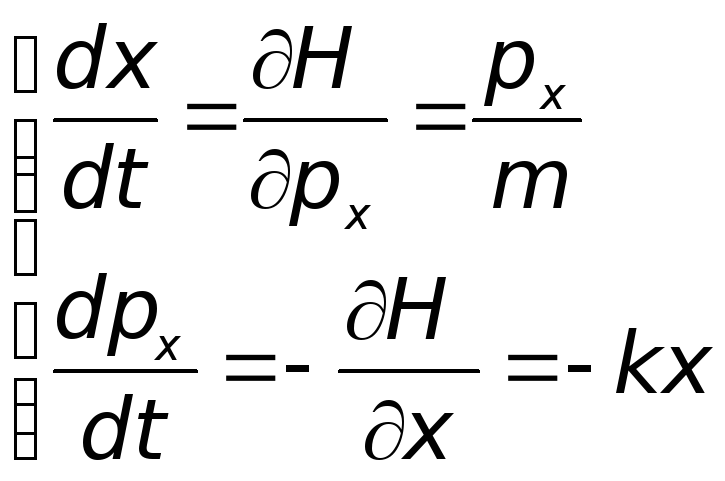
можно вывести рекурсивные формулы для положения тела и его импульса.

при этом непрерывная траектория движения заменяется ломаной линией с шагом t.

Мы видим, что метод МД - детерминистический: результат, полученный на определенном шагом определяется результатом, полученным на предыдущем шаге.

Численный алгоритм метода МД.

Пусть у нас есть система из N частиц, и движение каждой описывается дифференциальными уравнениями:

Нам нужно сгенерировать траекторию в фазовом пространстве, то есть подсчитать значения каждой частицы (их совокупность дает нам точку в фазовом пространстве) в момент времени:

.

Типичным методом численного решения дифференциальных уравнений является их превращение в конечно- разностные.

Заменим производную в отношением малого прироста функции к приросту аргумента (перемещение x за время t) ?. То есть для данной частицы в каждый момент времени t_n+1 скорость V_n+1:

.

Значит, каждое следующее положение определяется через предыдущее.

применив эти рассуждения к дифференциальному уравнению , получимформулы Эйлера для нахождения скорости и координаты как решений дифференциальных уравнений:

Допущением этих формул, как мы видим, является то, что на отрезке (t _n, t_n+1) скорость изменения функции X постоянна. Метод Эйлера - является ассиметричным - он продвигает решение на 1 шаг по времени t, используя при этом информацию о производных только в начальной точке интервала.

Существуют более точные методы:

Метод Эйлера - Камера (метод приближенно по последней точке)

Метод средней точки - использует для нового значения координаты среднюю на отрезке скорость

Метод полушага - использует допущение, что скорость на отрезке равна значению скорости в средней точке отрезка

Метод не является само стартующим, т. к. эти формулы не позволяют посчитать .

Можно посчитать:

.

Более точным является метод Верне.

Недостаток: необходимость другого метода для получения первых точек фазового пространства и вычисление скорости путем вычитания близких по величине значений. При этом теряются значимые цифры, и растет ошибка.

Эти недостатки отсутствуют в скоростной форме алгоритма Верне.

Метод Лимана и Шофилда:

не является само стартующим, однако считается лучше алгоритма Верне, т. к. лучше сохраняет энергию.

Метод предиктор- корректор - использует "предвидение" нового значения координаты.

Предиктор: позволяет вычислить ускорение, используя которое находим скорректированные значения:

Корректор:

Скорректированное значение используется для вычисления предсказываемого значения, а значит - новых предсказываемых значений. Эта процедура повторяется до тех пор, пока предсказываемое и скорректированное значения не будут близки.

Метод Рунге- Кутта позволяет повысить точность метода Эйлера вследствие экстраполяции в средней точке отрезка, а затем использовать центральную производную на всем отрезке (см. курс Численные методы).

Для различных динамических систем следует экспериментировать с разными алгоритмами расчета. Однозначных преимуществ не имеет ни один метод.

Практичне заняття 5.

На прошлом занятии мы рассмотрели основную идею детерминистического метода МД, для того, чтобы мы могли реализовать на компьютере модели идеального и реального газов и исследовать их поведение.

Цель исследования моделей - проверка основных газовых законов и исследование флуктуаций идеального и реального газов.

Методы исследования для модели идеального газа- методы МК и МД, для модели реального газа- метод МД.

Напомним, что в идеальном газе можно пренебречь взаимодействием между молекулами.

Модель идеального газа.

В предложенной модели движение молекул задается в виде одномерных блужданий, при которых через равные промежутки времени t (средний час между столкновениями) скорости изменяются случайно с помощью генератора случайных чисел по закону:

. (1)

Тут средний квадрат случайной функции

равен единице, что обеспечивает соотношение:

, известное из молекулярно- кинетической теории.

Соотношение (1), т. е. замена максвелловского распределения по V_x равномерным с сохранением среднего квадрата есть основным приближением модели.

Дальнейшая процедура адекватна реальной ситуации. Каждое столкновение со стенкой и переданный ей импульс подсчитывается и суммируется

а молекулы, столкнувшиеся со стенкой, двигаются по законам упругого столкновения. Например, если координата молекулы оказывается больше координаты правой стенкиL, то выполняется присвоение

Давление газа вычисляется по формуле .

Величина P флуктуирует, но с увеличением времени (и числа ударов) становится асимптотой. Фактически можно остановиться после 6 шагов для всех молекул, при

Алгоритм

Практичне заняття 6.

Алгоритм 5. Законы и свойства идеального газа. Основным параметром является радиус молекул, которые мы считаем твердыми двухмерными шарами (модель твердых сфер).

Метод расчета: МД то есть моменты результаты столкновений определяются самой системой. Для этого подсчитывается время столкновения всех молекул между собой и стенками и выбирается наименьшее. Стенки могут двигаться.

Алгоритм 5

Тестовый пример:

T=10 K, число молекул N=20, R=1e-10м (радиус молекулы), размеры сосуда 1е-8м; масса- молекулы кислорода.

***к пункту 4.

а) _i-_j; _i-_j; V_x=V_xi-V_xj; V_y=V_yi-V_yj;

a: =V_x²+V_y²

b: =2V_x+V_y

c: =^+^-4R²;

d: =b²-4ac

б) если а=0 и b=0 или (а и d то t _k:=-1;

в) если а=0 и b, то t _k:=-cb;

г) если а то:

1. если d=0, то t_k: =-ba

2. если d>0, то t₁: =(-b+)a

t₂: =(-b-)/(2a),

2.1) если t₁t₂, то t_k: =t₁=t₂

д) найти min время среди t_k: t_mol: =min(t_k).

***к пункту 3

а) если V_xi>0, то t₁: =(L_x-R-X_i)/V_xi

б) если V_xi<0, то t₁: =(x₀+R-x_i)/(V_xi-V_st)

(x₀ и V_st- координата и скорость левой стенки)

в) если V_yi>0, то t₂: =(L_y-R-y_i)/V_yi

г) если V_yi<0, то t₂: =(R-y_i)/V_yi

д) если t₁<t₂ то t_i: =t₁, иначе t_i: =t₂

е) найти min среди t_i: t_st: =min(t_i)

**** к пункту 6.

а) если dt=t_st, то:

1. если _rV_xrdt-R, то Vnx: =-V_xr+2V_st иначе V_nx: =V_xr;

2. если _r+V_xrdt+RL_x, то V_nx: =-V_xr иначе V_nx: =V_xr

3. если _r+V_xrdt+RL_x, то V_nx: =-V_xr иначе V_nx: =V_xr

4. если _r+V_yrdt-R; или _r+V_yrdt+RL_y, то V_ny: =-V_yr, иначе V_ny: =V_yr.

б) если dt=t_mol, то

n_k: =_k+V_xkdt; n_k: =_k+V_ykdt

n_l: =_l+V_xldt; n_l: =_l+V_yldt;

S_x=n_l-n_k; S_y: =n_l-n_k;

S=;

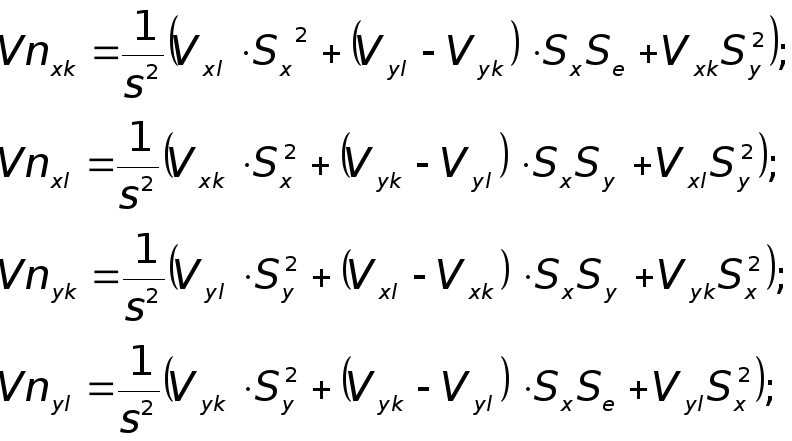
Задание:

1. Исследовать воздействие межмолекулярных столкновений на необратимость.

Все реальные процессы необратимы, что, в частнрсти, связано с нестойкостью фазовых траэкторий макросистем относительно малых возмущений. Если в какой- то момент поменять скорости всех молекул на противоположный, даже минимальное возмущение не даст им двигаться "след в след" и оказаться в начальном микросостоянии. Если выполнить это для пркдыдущего алгоритма- модели идеального газа, то мы увидим, что столкновение с гладкими стенками материальных точек- молекул идеального газа не вносит вклад в необратимость процесса. Эта проблема решается в данном алгоритме модели твердых сфер. Проверить это практически.

2. Проверить уравнение адиабаты для двухмерной модели реального газа.

При включении в модель медленного движения стенки можно исследовать уравнение адиабаты (Т(V)).

Температура рассчитіваеться через средний квадрат скорости молекул.

3. Построить распределение Максвелла:

а) найти среднеквадратичную скорость

б) ввести условную верхнюю границу скорости

в) /20;

г) определить, в какой интервал попадает скорость каждой молекулы и построить гистограмму.

Єто дает возможность проследить за кинетикой установлениях статистического равновесия. Если задать начальные скорости одинаковыми по величине и направлению, по мере столкновений гистограмма из прямоугольника превратится в распределение Максвелла.

Примечание: напомним, что распределение Максвелла есть частный случай распределения Максвелла- Больцмана, когда нас, интересует вероятность скорости или импульса молекул идеального газа.

Практичне заняття 7.

Тема: Проверка закона Ома на модели одномерных блужданий электронов в электрическом поле случайными столкновениями (МК - метод).

Физическая постановка задачи

Поведение металла в электрическом, тепловом или магнитном полях достаточно точно описывается классической электронной теорией Друзе - Лоренца (начало 20 века).

Основные положения электронной теории:

1. Металл состоит из ионного каркаса и электронного газа: свободные электроны не

связаны с конкретными ионами. Последние обеспечивают нейтральность системы и

не дают электронам разлетаться.

2. Движение электронов - поступательное движение свободных частиц между столкновениями. При столкновении электрон "забывает" предысторию, т. е. сразу после столкновения средняя его векторная скорость 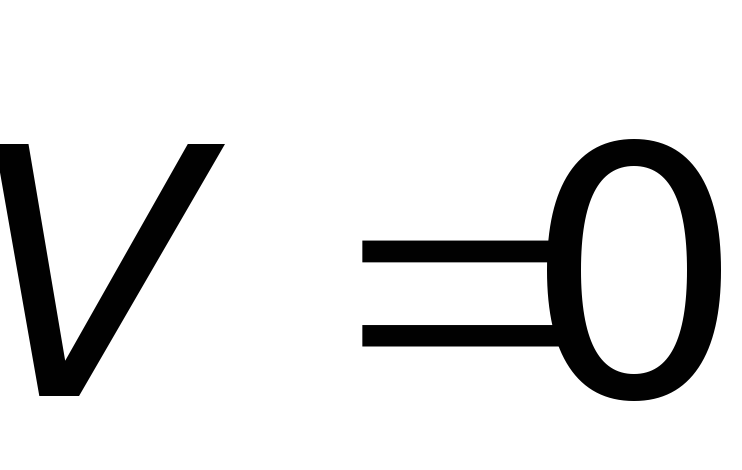, а средний квадрат скорости определяется условием термодинамического равновесия:

; где T- температура в месте столкновения

3. Вероятность столкновения электрона на протяжении малого времени dt пропорциональна этому времени и равна

, где

τ- среднее время свободного пробега (время релаксации системы), а формула (2) справедлива при dt<<τ (для большинства металлов τ ≈10^-14с).

Найдем вероятность того, что электрон не испытывает столкновений на протяжении времени t. Разобьем весь временной интервал на отрезки . Искомая вероятность равна произведению вероятностей на каждом отрезке:

(согласно математической формуле ).

Среднее время до столкновения:

; где

i- вероятность избежать столкновение на протяжении t,

ii- вероятность столкновения на следующем интервале dt.

Аналогично: (обратим внимание на множитель 2)

4. Согласно закону Ома, действие постоянного электрического поля на металл вызывает постоянный электрический ток, пропорциональный средней скорости зарядов. Т. е. скорость, а не ускорение пропорционально силе. Этот "парадокс" объясняется столкновениями электронов с тепловыми и структурными дефектами, что необходимо учитывать в модели через коэффициент электропроводности.

Примечание*. Закон Ома в дифференциальной форме:

Пусть на электроны газа в металле действует поле напряженности Е. Тогда на каждый электрон действует внешняя сила , т. е. каждый электрон между столкновениями должен двигаться равноускоренно.

Пусть t- время после последнего столкновения;

V₀- скорость после последнего столкновения.

Тогда: (3)

Средняя скорость: (4) поэтому:

(5)

Плотность тока:

(6)

В итоге:

, где (7)

σ- электропроводность (-удельное сопротивление). Отсюда можно получить обычную, интегральную форму закона Ома:

учитывая, что

l- длина проводника;

S- площадь сечения.

Модель для компьютерного эксперимента:

- модель одномерного блуждания электронов со случайными столкновениями в электрическом поле. В данном простейшем варианте модели принимаем, что в момент столкновения электрон полностью теряет скорость и начинает новый цикл ускорения с ø.

Основной параметр модели - среднее время между столкновениями τ. Электрон двигается равномерно между столкновениями. Время, пройденное им без столкновений задается генератором случайных чисел по правилу:

Исследуемые параметры модели:

1. Выводиться график зависимости средней скорости от времени. Он имеет осциллирующий характер и через несколько сотен столкновений (К- в алгоритме - это количество столкновений) выходит на асимптотическое значение, которое следует зафиксировать в памяти плюс значение Е напряженности поля (объявить массив).

2. Процедура 1 проводиться для ряда значений Е (n=50), и строиться график График должен иметь форму прямой, чтобы подтвердить закон Ома:.

Алгоритм

Найти новую координату электрона- точку столкновения

Тестовый пример:

Е=0; Е=100 В/м; =10^-14 с.

Практичне заняття 8.

Проверка закона Джоуля - Ленца (метод МК)

Физическая модель:

Во время столкновения электроны передают решетке свою энергию, полученную за счет их ускорения внешним полем. Найдём энергию, которая выделяется за единицу времени в единичном объёме. Рассматриваемый объём находиться в электрическом поле с напряженностью . Для этого найдём среднее изменение энергии электрона во время столкновения:

где (смотри предыдущее занятие).

Следовательно:

;

отсюда:

.

Численная модель.

В основу модели положено использование ГСЧ для времени между столкновениями электронов с решеткой.

Считаем, что в момент столкновения электрон теряет всю энергию, полученную от электрического поля.

После усреднения по множеству столкновений находим среднюю энергию, которую электрон отдаёт кристаллической решетке за единицу времени. Умножив её на концентрацию электронов получим мощность тепловых потерь за единицу времени.

Алгоритм реализации модели

Тестовый пример: E=0, E=100 B/м, =10^-14с.

Задание: проверить квадратическую зависимость тепловых потерь от напряженности поля.

Убедиться, что коэффициент пропорциональности в этой зависимости равен , т. е. совпадает с электропроводностью металла.

Следующая модель, которую мы рассмотрим -

Динамика электронного газа (метод МД)

Идея:

Детерминистические модели динамики электронного газа основаны на численном решении в конечных разностях кинетического уравнения для среднего импульса электронов.

В амоделе нужно учитывать дополнительное поле, которое возникает вследствие накопления поверхностных зарядов, т. е. численным методом решают систему двух уравнений.

Предметом исследования модели является Эффект Холла.

На экран выводятся:

• График зависимости напряженности поперечного поля от времени при фиксированной индукции магнитного поля. Это даёт возможность наблюдать процесс установления стационарного поперечного поля.

• Проверяется закон Холла

- постоянная Холла.

• Проверяется совпадение R_н с теоретическим значением

Физическая модель:

Эффект Холла- возникновение поперечной разности потенциалов в проводнике с током под действием магнитного поля.

Холл открыл это явление в 1879 году, проводя эксперименты по поиску магнитного сопротивления. Его логика была довольно простой: под действием магнитного поля (силы Лоренца) подвижные носители зарядов должны отклоняться от движения, направленного вдоль силовых линий внешнего электрического поля- источника тока. Это отклонение должно уменьшать скорость Дрейка носителей заряда. Поэтому сопротивление (U/I) должно возрастать по мере увеличения индукции магнитного поля. Но в эксперименте выяснилось, что сопротивление не зависит от магнитного поля. Однако появилась поперечная разность потенциалов, пропорциональное индукции магнитного поля, плотности тока и ширине проводника:

,

R_н называют постоянной Холла.

Поперечная разность потенциалов означает существование поперечного электрического поля с напряженностью

.

Пояснение эффекта Холла классической электронной теорией элементарно:

После включения магнитного поля электроны, дрейфующие против силовых линий электрического поля начинают отклоняться (под действием силы Лоренца) к краям пластины (см. рис.1)

Р

z

ис.1

Это приводит к разделению зарядов (накопление электронов с одной стороны и оголение ионов с другой).

При этом возникает и увеличивается поперечное электрическое поле.

Накопление зарядов и рост поперечного поля продолжается, пока сила поперечного поля

(-е) Е_y не скомпенсирует силу Лоренца . После этого сила тока возвращается к прежнему значению, т. е. магнитного сопротивления наблюдаться не будет. Время установления стационарного режима- порядка- времени релаксации электронной подсистемы, т. е. очень мало.

В стационарном случае проекция результирующей силы на ось =0:

где B_x=0; - условие стационарности.

Перейдём к плотности тока:

тогда

- постоянная Холла.

Мы видим, что эффект Холла чувствителен к заряду носителей тока.

Эта теория выполняется лишь для щелочных металлов, для других R_н зависит от

И может менять знак со сменой магнитного поля.

Кроме того, для многих металлов и, в особенности, полупроводников R_н зависит от температуры. Эти явления классическая электронная теория не поясняет.