5.3.3. Чисельні методи розв’язування задач нелінійного програмування

Обмежимося розглядом задач типу: мінімізувати функцію

за наявності обмежень

(5.24)

де - випуклі функції,- випукла замкнута множина, яка має внутрішні точки.

Сформульовану задачу називають основною задачею випуклого програмування. Вважаємо, що множина , визначена умовою (5.24), задовольняє умову регулярності Слейтера:

існує така точка що

(5.25)

Функцію

(5.26)

де називаютьфункцією Лагранжа для основної задачі випуклого програмування. Пара називаєтьсясідловою точкою функції на множиніякщота

(5.27)

для всіх

Значну роль в теорії випуклого програмування відіграє наступне твердження, яке називається теоремою Куна-Таккера:

Точка є розв’язком основної задачі випуклого програмування на множині, який задовольняє умову Слейтера, тоді і тільки тоді, коли існує така точкащо парає сідловою точкою функції Лагранжа.

У випадку, коли на область накладені додаткові обмеження, можна отримати необхідну і достатню умову сідловок точки. Справедливою є наступна теорема.

Теорема

Якщо функціїосновної задачі випуклого програмування неперервно диференційовані на множині то для того, щоб парабула сідловою точкою функції Лагранжа на множинінеобхідно і достатньо виконання умов

(5.28)

Оскільки множина , за означенням, задовольняє умову регулярності Слейтера, то умови (5.28) є необхідними і достатніми умовами існування розв’язкуосновної задачі випуклого програмування у випадку диференційованості функційБезпосереднє застосування теореми Куна-Таккера чи наведеної теореми для знаходження розв’язкуосновної задачі опуклого програмування пов’язано з великим обсягом обчислень, тому є малоефективним. Проте ці теореми можна використати для перевірки точок«підозрілих» на оптимальність. Для цього достатньо з умов (5.28) за умови заданоговизначити. Якщо такий розв’язокіснує, то парабуде сідловою точкою функції Лагранжа, а- розв’язком відповідної задачі випуклого програмування.

Приклад

Перевірити, чи є точка розв’язком наведеної нижче задачі, якщо є, то знайти сідлову точку Лагранжа.

Складемо функцію Лагранжа

Для неї маємо

Тобто Далі покладемо

Оскільки то,Таким чином пара точок

є сідловою точкою функції Лагранжа.

Багато алгоритмів чисельного розв’язку задач нелінійного програмування реалізує різні методи одного з двох підходів до задач умовної оптимізації – методів пуску та методів штрафних функцій. З методів спуску розглянемо метод можливих напрямків Зойтендейка. Для опису цього методу введемо деякі означення.

Вектор називається напрямком спадання функціїв точці, якщо існують числатакі, що для всіх, які задовольняють умовивиконується нерівністьЯкщо множина напрямків не порожня, то вона є конусом (множинаназиваєтьсяконусом з вершиною в точці якщо поряд зі своєю точкоювона містить також всі точкитипуЯкщо функціядиференційована в точці, то множина напрямків спадання буде простором.

Нехай - певна множина зВекторназиваєтьсяможливим напрямком в точці , якщо існує число можливих напрямківтаке, щоза умови. Множина можливих напрямків в точціє внутрішньою точкою множини, то цей конус є простором

Розглянемо основну задачу випуклого програмування:

за умови

В припущенні, що множина задовольняє умову регулярності Слейтера, а функціївипуклі і неперервно диференційовані.

Нехай Метод можливих напрямків базується на тому, що серед всіх можливих напрямків в точцівибирається напрямок найбільшого спадання функціїі здійснюється спуск впродовж цього напрямку до точки, далі, виходячи з точки, процес повторюється. В цьому випадку доводиться розв’язувати задачу вибору напрямку спуску та задачу вибору кроку за цим напрямком. Наведемо короткий опис методу. Нехай- довільне мале число,де- задана точність,. Визначимо длясукупність індексів

Множин допустимих векторів

та множину пар

Слід мати на увазі, що - не порожня множина. В основі алгоритму визначення напрямку спуску знаходиться таке твердження:

Для того, щоб напрямок був можливим в точці, необхідно, щоб і достатньо, щобхоча б для одного

Припустимо, що в результаті - ї ітерації обчисленіі множинаЩоб виконати наступну ітерацію, розглянемо задачу

(5.29)

Це задача лінійного програмування. Для приведення її до основного вигляду покладемо Тоді задача (5.29) прийме вигляд

(5.30)

Розв’язуючи цю задачу, знайдемо а також вектор напрямку спускуНехайтоді:

а) Якщо то визначимо числоабо з умови:

якщо то вибираємо, або коли це простіше, з умови

де

Після того як вибрано, покладемообчислюємоі переходимо до наступної ітерації.

Слід відмітити, що якщо точка знаходиться далеко від точки, що мінімізує, то множиниможуть різко змінюватися із зміною. Це призводить до так званого зигзагоподібного руху. Для його уникнення, можна вибрати як напрямок спуску певний напрямок спадання, який не змінює множину. Замітимо, що якщо- порожня множина, то напрямок спуску визначають рівністю

б) Якщо ж то припускаємовибираємо множинуі переходимо до наступної ітерації.

Обчислення припиняються тоді, коли Встановлено, що якщо множинаобмежена, послідовність, побудована за наведеним вище алгоритмом та мінімізуючи точкаєдина, тоОбґрунтуванням закінчення обчислень за умови достатньо малого, знайденого в процесі розв’язку задачі (5.29), є наступна теорема.

Теорема

Всяка точка для якої задача

визначає величину є розв’язком основної задачі випуклого програмування.

Приклад

Оскільки тоДля визначенняприходимо до задачі лінійного програмування

яку приводимо до канонічного вигляду. Для цього покладемо і, скориставшись співвідношеннями (5.30), замінюємо в них нерівності рівностями шляхом введення нових змінних

Розв’язуючи цю задачу симплекс-методом, знаходимо Оскількито вважаємоі маємоТобтоі з рівностіотримуємотаким чином,таТому маємо задачу

розв’язуючи яку, знаходимо тобтота

Тобто

Одним з найпоширеніших методів розв’язування задач нелінійного програмування є метод штрафних функцій. Його ідея полягає в приведенні задачі умовної мінімізації функції до послідовності задач безумовної мінімізації певних допоміжних функцій. Розглянемо одну з найпростіших схем цього методу –метод зовнішніх штрафних функцій. Обмежимося основною задачею випуклого програмування в такій формі

за умови ,

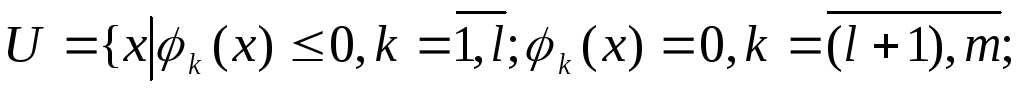(5.31)

В припущенні, що множина обмежена і задовольняє умову регулярності Слейтера, а функціївипуклі і неперервно диференційовані на певній множині. Послідовність функцій, визначених на множині, яка містить множину, називаютьштрафною послідовністю функцій множини , якщо

Користуватимемося найпоширенішою послідовністю штрафних функцій

де

У цьому виразі

Покладемо

і припустимо, що кожна з функцій досягає свого найменшого значенняв певній точці

Виявляється, що за виконання умов, накладених на функції та множину, задача (5.31) має розв’язок, причому

Слід зауважити, що кожна з функцій на множиніє випуклою, неперервно диференційованою функцією і, відповідно, для визначення точокта чиселможна застосувати всі розглянуті вище методи безумовної мінімізації. Метод штрафних функцій успішно застосовується також для розв’язку більш загальних задач нелінійного програмування. В методі штрафних функцій неможна вимагати більшої точності за умови недостатньо великого значення, тому в процесі розв’язування допоміжних задач мінімізації функціїможна обмежитися двома наближеннями за методом найшвидшого спуску.

Приклад

За штрафну функцію візьмемо В околі початкової точкисправедливими є рівності

Тому покладемо

Для перевірки на випуклість функції складемо для неї матрицю з других похідних

A = =.

Оскільки то за критерієм Сільвестера матрицяє додатно визначеною і, відповідно, функціявипукла. Для визначення мінімумускористаємося методом найшвидшого спуску. Обчислюючи градієнт функціїв точцізнайдемо. Для визначення наступного наближення покладемоі визначимоз умови

Знаходимо і, тим самим наступне наближення

Слід зауважити, що тому

Аналогічно попередньому знаходимо Тому

Вважаємо