залык / Вопрос 8

Лекция 3

Описание линейных дискретных систем.

Исходя из алгоритмов решаемых задач и требований к скорости цифровой обработки выделяют первичную и вторичную обработку информации.

Первичная – получила термин цифровой обработки сигнала, т.к. предполагает помимо преобразования входных сигналов в цифровую форму, еще и выделение полезных сигналов на фоне помех, декодирование, демодуляцию сигналов, оценку их параметров, спектральные преобразования, а также задачи их обработки.

Основные методы для решения перечисленных задач – это цифровая фильтрация, корреляционный анализ и др.

Вторичная – решает задачи распознавания образцов на основе анализа спектров сигналов, полученных в процессе ЦОС, а так же задачи управления, цифрового моделирования, контроля и диагностики, обработки статистических данных и др.

Таким образом, ЦОС в основном включает в себя цифровую фильтрацию и спектральный анализ.

Фильтрация осуществляется цифровыми фильтрами с бесконечной импульсной характеристикой (БИХ) и конечной импульсной характеристикой (КИХ). Строиться они могут по рекурсивной схеме и нерекурсивной схеме.

В любом случае цифровой фильтр – это система обработки сигналов. В большинстве случаев – это линейные системы.

Описание линейных дискретных систем во временной области.

Определим под понятием системы обработки сигналов – объект с одним входом, задающий воздействие и одним выходом с реакцией. В общем случае их взаимосвязь в операторной форме Y=F(X), где X, Y – множество воздействий и реакций. F – оператор, определяющий характер математической операции при отображении множества X в Y.

Соотношение вход-выход для линейной системы описывается линейным уравнением, т.е. в правой части уравнения Y=F(X) стоят только линейные алгебраические операции сложения, вычитания и умножения на весовой коэффициент.

Линейная система называется дискретной если воздействие и реакция представляют собой дискретные сигналы – последовательности отсчетов x(nT) и Y(nT), как вещественные, так и мнимые

Рис. Общая схема обработки сигналов линейной дискретной системой

Во временной области линейная дискретная система описывается импульсной характеристикой (ИХ).

ИХ h(nT) ЛДС называется ее реакция на единичный цифровой импульс U₀(nT) при нулевых начальных условиях.

Рис. Единичное воздействие и реакция

Признаком нулевых начальных условий является отсутствие реакции при отсутствии воздействий

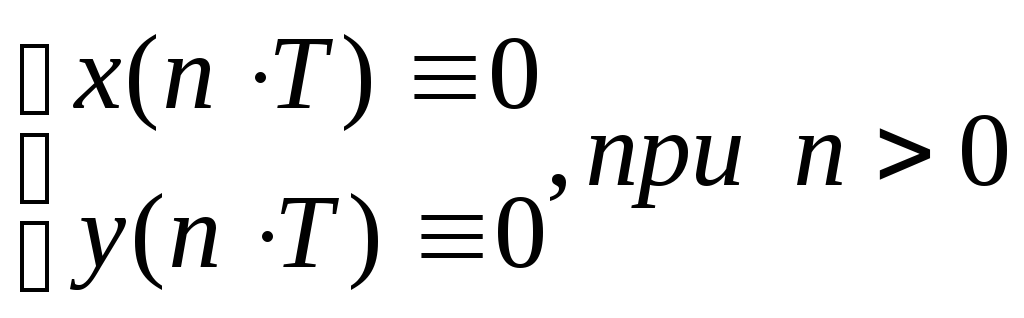
Помимо импульсной характеристики при описании ЛДС во временной области используют переходную характеристику g(nT). Это реакция ЛДС на единичный цифровой скачок U₁(nT) при нулевых начальных условиях

а) б)

Рис. Виды воздействий: единичный импульс (а) и единичный цифровой скачок (б)

Во временной области соотношение вход-выход ЛДС описывается линейными уравнениями:

- формулой свертки, если используется импульсная характеристика;

- разностным уравнением, если используются параметры ЛДС.

Формула свертки.

Уравнение взаимосвязи между входными x(nT) и выходными y(nT) сигналами, для ЛДС, заданной своей импульсной характеристикой h(nT).

, (1)

где h(nT – mT) – импульсная характеристика, задержанная на m – периодов дискретизации. Линейное уравнение (1) называют формулой свертки. Согласно ей реакция y(nT), вычисляется как дискретная свертка воздействия x(nT) и импульсной характеристики h(nT). Через стандартное условное обозначение свертки формулу (1) можно представить

y(n) = x(n) · h(n).

В результате можно получить второй вариант формулы свертки

.

Таким образом, для нормированного времени формула свертки

Пример: Вычислить реакцию ЛДС по формуле свертки, если импульсная характеристика и воздействие заданы графически. Требуется определить до 8 отсчетов.

Рис. Заданные графически импульсная характеристика (а) и воздействие (б)

Решение:

Рис. Результат вычисления по формуле свертки

Рис. Механизм вычисления, представленный графически

Механизм вычислений сигналов можно представить как последовательное вычисление сумм локальных произведений двух последовательностей – импульсной характеристики и воздействия.

Одну из последовательностей можно зафиксировать, а другая может зеркально отображаться относительно оси ординат и скользить слева направо по оси времени.

Вычисление прекращается, когда все локальные произведения окажутся равными нулю, при т.н. «расхождении» перемножаемых последовательностей.

В примере при m=5 они расходятся.

Отсюда выводы:

- если длительность воздействия и/или импульсной характеристики бесконечна, то длительность реакции бесконечна

- если длительность воздействия x(nT) и импульсной характеристики h(nT) конечны и равны N·T и M·T, то длительность реакции y(nT) также конечна и равна L·T, где L=N+M-1.

Тогда при конечных воздействиях и импульсной характеристики формула свертки

.