Новая папка / Упругое рассеяние электронов

3

Упругое рассеяние электронов

Рассеяние электронов без изменения энергии при прохождении через вещество лежит в основе дифракционного метода анализа атомно-кристаллической структуры и методов просвечивающей электронной микроскопии, включая методы дифракционной электронной микроскопии.

Упругое рассеяние первичного пучка электронов связано с их движением в поле электрического потенциала атомов исследуемого материала.

Доля упругого рассеяния повышается с увеличением заряда ядра атома Z (рис. 1.б).

Электрический потенциал в некоторой точке атома складывается из

• положительного потенциала от ядра Ze/r

и

• отрицательного потенциала от электронной оболочки.

Для простоты можно принять равномерное распределение заряда электронной оболочки внутри сферы радиуса R (рис. 1,а). В таком случае потенциал от отрицательного заряда внутри этой сферы φ_ должен быть меньше, чем потенциал от сосредоточенного положительного заряда ядра (рис. 1,б). Это приводит к тому, что в данной области нет компенсации положительного потенциала и потенциал атома описывается выражением

(1)

Компенсация потенциала φ_ат=0 будет за пределами сферы радиуса R.

Общее выражение для атомной функции рассеяния любого типа излучения получается через преобразование Фурье распределения материи, рассеивающей данное излучение (рис. 1). Если для рентгеновских лучей это было распределение электронной плотности ρ(r) (2), то для рассеяния электронов это будет распределение электрического потенциала φ(r) (3):

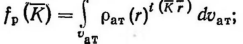(2)

(3)

Рис. 1. Представление атома в виде сферического конденсатора:

а — распределение заряда; б — изменение потенциала от ядра φ(r)₊ и потенциала от электронной оболочки φ(r)_ и результирующего потенциала φ(r)

Рис. 2. Атомная функция рассеяния электронов в зависимости от параметра для золота, меди, углерода

Уравнение Пуассона связывает распределение потенциала φ(r) с распределением электрических зарядов ρ₊(r) и ρ_(r):

(4)

Распределение ρ_(r) можно получить как Фурье-трансформанту атомной функции рассеяния рентгеновских лучей из выражения (2):

(5)

Поскольку в выражении (4) вместе фигурируют распределения р_ и р+, целесообразно их представить одинаковым образом в форме выражения (5).

Считая заряд ядра сосредоточенным в точке, можно представить его распределение через δ-функцию: ρ₊(r) =δ(r), причем δ(r)dv_at=Z, Фурье — трансформанта от заряда ядра будет иметь вид

(6)

Поскольку заряд ядра сосредоточен в точке, f_+z не будет зависеть от направления (в электронных единицах f_+Z = Z). В действительности рассеяние рентгеновских лучей на ядре пренебрежимо мало по сравнению с рассеянием на электронах, так как амплитуда рассеяния рентгеновских лучей обратно пропорциональна массе заряженной частицы.

Представим функцию δ(r) через интеграл Фурье в виде

(7)

Подставим выражения (5) и (7) в уравнение (4):

(8)

Обращая уравнение (3 ), получим

(9)

Дважды дифференцируя подынтегральное выражение (9) по r, получим

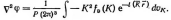(10)

Легко видеть тождественность структуры интегралов в выражениях (8) и (10) для ν²φ; это позволяет записать уравнение, из которого сразу получаются выражения для атомной функции рассеяния электронов:

(11)

и

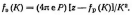(12)

Окончательно

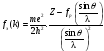
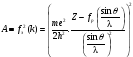(13)

Значения f_Э(K) приводятся в таблицах.

В формуле (13), кроме зависимости f_r от аргумент входит во второй степени. Поэтому за единичное рассеяние принимают рассеяние от протона в определенном направлении для 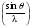=0,1 * 10⁸ см^-1.

Для перехода от табличного значения f_T в протонных единицах к абсолютной величине атомной амплитуды рассеяния надо знать коэффициент перехода, т. е. амплитуду рассеяния электронов протоном, когда z = 1, f_p=0, sin·θ/λ=0,1.10⁸ см^-1:

(14)

Характер зависимости f_э(sin·θ/λ) виден из рис. 9. Интенсивность рассеяния пропорциональна f_э², следовательно, спад интенсивности с увеличением sin·θ/λ будет резким, так как в формулу эта величина входит в четвертой степени. В связи с таким характером зависимости в анализе интенсивности рассеяния электронов обычно не учитывают температурный фактор.

Зависимость f_э от природы атомов z оказывается различной в разных интервалах sin·θ/λ, поскольку в уравнении (13), кроме r, в явном виде имеется f_p, которая является и функцией z, и функцией sin·θ/λ Только при больших значениях sin·θ/λ, когда f_r мало, f_Э пропорционально Z; при малых значениях sin·θ/λ зависимость менее сильная, что создает несколько более благоприятные условия для обнаружения легких атомов, чем в случае рассеяния рентгеновских лучей.

Последняя важная особенность рассеяния электронов связана с тем, что амплитуды их рассеяния оказываются на три порядка больше амплитуд рассеяния рентгеновских лучей (а интенсивность в 10⁶ раз). С этим связана возможность получения дифракционных картин при очень малых количествах вещества (например, от отдельных частиц или пленок малой толщины).

/var/www/studfiles2/data/www/download/2706/299/Y4KhHEgjOr.Eso0