Новая папка / Лекция №02 Геометрическая оптика

Электронная микросокпия. Лекции И.Е. Котенко Thursday, 18 July 2019 г.

Лекция №2

Основные понятия геометрической и волновой оптики

Представления геометрической оптики справедливы лишь в той степени, в которой явлениями дифракции и интерференции можно пренебречь. Геометрическая оптика является предельным случаем волновой оптики, когда длина волны существенно меньше размеров объекта.

Физической основой геометрической световой оптики является изменение направления светового луча на границе раздела двух сред, что выражается в форме закона преломления:

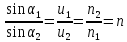(1)

где

• ₁ — угол падения светового луча;

• ₂ — угол преломления;

• и₁ и и₂ — фазовые скорости световых волн в среде 1 и 2 соответственно;

• n₁ и п₂ — показатели преломления соответствующих сред;

• n —относительный показатель преломления.

Простейшим приложением закона преломления является рассмотрение преломления световых лучей на криволинейных поверхностях, примером которых являются ограничивающие поверхности стеклянных линз.

Оптические свойства линзы характеризуются, в первую очередь, ее фокусным расстоянием, т. е. расстоянием от линзы до точки, в которой пересекаются падающие на линзу параллельные лучи, т.е до так называемой фокальной точки, или фокуса, линзы.

Рис. 1 Схема формирования изображения тонкой линзой

Величина фокусного расстояния f зависит от радиуса кривизны преломляющих поверхностей и показателя преломления материала линзы:

• чем меньше радиус кривизны и

• чем больше показатель преломления,

• тем меньше фокусное расстояние линзы, тем она сильнее.

Зная фокусное расстояние f линзы, можно определить взаимное расположение объекта и его изображения, создаваемого этой линзой. Если

а — расстояние от объекта до линзы,

b — расстояние от линзы до изображения (рис. 1), то

⁽²⁾

Уравнение (2) носит название основной формулы линзы. Эта формула получена на основании закона преломления (1) в предположении, что лучи, принимающие участие в создании изображения,

• во-первых, образуют малые углы с оптической осью линзы и,

• во-вторых, удалены от оси на малые расстояния.

Такие лучи называются параксиальными, а выполнение указанных условий (так называемая Гауссова диоптрика) обеспечивает получение стигматического изображения, когда каждая точка объекта изображается также точкой.

С помощью формулы (2) нетрудно определить поперечное увеличение линзы М (которое мы в дальнейшем будем называть просто увеличением)

(3)

Из формулы (3) видно, что большие увеличения (при заданном расстоянии от линзы до изображения) дает короткофокусная линза, при этом объект должен быть расположен вблизи фокуса.

Прежде чем приступить к рассмотрению принципов электронной оптики и их реализации в электронных линзах и других электронно-оптических устройствах, целесообразно напомнить некоторые основные понятия геометрической и волновой оптики, которые будут использоваться в дальнейшем.

Определимся с терминологией.

Совокупность лучей образует пучок.

Волна – процесс распространения колебаний. Световая волна обладает осевой симметрией, являясь в то же время поперечной. Волны, например, на поверхности воды такой симметрией не обладают, так как колебания частиц воды происходят только в вертикальной плоскости.

Волна, распространяясь от источника колебаний, охватывает все новые и новые области пространства.

Волново́й фронт (фазовый фронт)— это поверхность, отделяющая в определенный момент времени область возмущения от области покоя Волновой фронт является частным случаем волновой поверхности.

Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью ( поверхностью постоянных фаз, фазовой поверхностью). Волновой фронт может быть плоским, сферическим или иметь более сложную форму. Каждая точка фронта является источником вторичных волн, которые через короткое время образуют фронт волны на новом месте.

Волновых поверхностей можно провести бесчисленное множество, а волновой фронт в каждый момент времени - один.

Скорость распространения гармонической волны называется фазовой скоростью.

Фазовый фронт — геометрическое место точек, имеющих одну и ту же фазу.

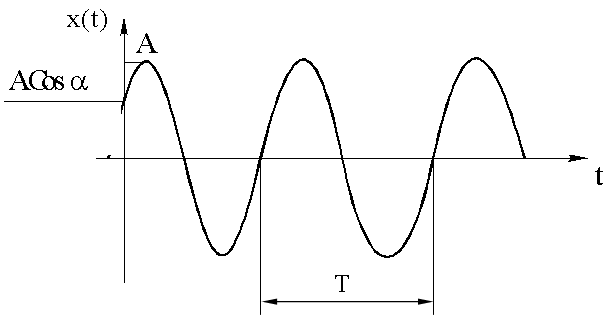
Именно фронт волны перемещается со скоростью равной фазовой скорости волны. В случае одномерной синусоидальной волны уравнение волновой поверхности имеет следующий вид:

Этому условию в каждый момент времени удовлетворяет только одна точка оси ОХ, координата х которой равна:

Различным значениям фазы волны φ соответствуют различные волновые поверхности, каждая из которых в одномерных волнах вырождается в точку. Из последней формулы видно, что волновые поверхности с течением времени перемещаются в среде со скоростью, равной , т.е. фазовой скоростью, которая равна

Таким образом, для синусоидальной волны скорость распространения поверхности постоянной фазы совпадает со скоростью распространения волны.

ВОЛНОВОЙ ВЕКТОР - вектор k, определяющий направление распространения и пространственный период плоской монохроматической волны

),

где

• A₀ - амплитуда волны,

• φ₀- фаза волны

• w- круговая частота,

• r - радиус-вектор.

Модуль волнового вектора называется волновым числом , где λ - пространственный период или длина волны.

В направлении волнового вектора происходит наибыстрейшее изменение фазы волны φ=kr-ωt+φ₀, т.е. k=, поэтому оно и принимается за направление распространения.

Фаза колебания - это дробная часть t/T периода T, на которую t сдвинуто относительно произвольного начала координат.

Началом координат обычно считается момент предыдущего перехода функции через нуль в направлении от отрицательных значений к положительным.

Циклической частотой называется число циклов колебаний в единицу времени .

Угловой частотой называется число циклов колебаний в интервале времени равному 2π единицам, w=2πf=[] .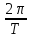

Величина (wt+φ) называется фазой колебания. Она характеризует состояние колебания в любой момент времени t.

Для таких колебаний как:

• ),

• )

• ,

или волн, распространяющихся в одномерном пространстве:

• ),

• ),

• ,

или волн, распространяющихся в трехмерном пространстве (или пространстве любой размерности) фаза колебаний определяется как аргумент этой функции, описывающей гармонический колебательный процесс или монохроматическую волну.

Поскольку синус и косинус совпадают друг с другом при сдвиге аргумента (то есть фазы) на π/2 то во избежание путаницы лучше пользоваться для определения фазы только одной из этих двух функций, а не той и другой одновременно.

Фазой считают аргумент косинуса, а не синуса.

То есть,

• для колебания в точке фаза φ=,

• для волны в одномерном пространстве ;

• для волны в трехмерном пространстве или пространстве любой другой размерности: ,

где

• ω— угловая частота ,

• t— время,

• — фаза при t=0 - начальная фаза;

• k - волновое число,

• x - координата,

• k - волновой вектор,

• x - набор (декартовых) координат, характеризующих точку пространства (радиус-вектор).

Фаза выражается в угловых единицах (радианах, градусах) или в циклах (долях периода):

1 цикл = 2π радиан = 360 градусов.

/var/www/studfiles2/data/www/download/2706/299/4WjDqtuGrx.4oit 8