Новая папка / Определение фазы по ее электронограмме

9

Определение фазы по ее электронограмме.

http://studopedia.net/10_91029_lektsiya-.html

Анализ геометрии точечных электронограмм проводится для решения нескольких задач. Одной из них является определение фазы, которой соответствует данная электронограмма. Такая задача, в частности, встречается при электронно-микроскопическом исследовании для выявления кристаллографической природы наблюдаемых фаз. Анализ электронограммы в этом случае состоит в вычислении межплоскостных расстояний d/n, соответствующих набору рефлексов на электронограмме. По полученным значениям d/n можно проидентифицировать фазу сопоставлением с набором табличных значений d/n. Точность определения d/n по электронограммам относительно невысокая. Дополнением, увеличивающим достоверность идентификации, является измерение углов между векторами соответствующими углами j_{HH`</sub>, между векторами обратной решетки, принадлежащими одной плоскости. Измеренные углы j<sub>HH`} можно затем сопоставить с вычисленными углами между плоскостями для предполагаемой фазы (если ее решетка известна). Если рефлексов на электронограмме мало, как это часто бывает при электронно- микроскопических исследованиях, для увеличения достоверности идентификации необходимо снять по меньшей мере еще одну электронограмму для другой ориентировки данной фазы.

Определение ориентировки.

Весьма распространенной задачей является определение ориентировки кристалла с известной структурой. В этом случае необходимо проиндицировать электронограмму образца, определенным образом ориентированного по отношению к внешней системе координат – ось пучка и плоскость электронограммы. Электронограмма соответствует отражениям от плоскостей зоны, ось которой <u₁u₂u₃>, параллельная электронному пучку, находится из уравнения зональности (нулевая Лауэ-зона):

 (1)

здесь H_jⁱ – индексы i-того узла, принадлежащего данной плоскости обратной решетки.

Выбрав два узла, лежащие на пересекающихся узловых прямых, можем сопоставить соответствующие им межплоскостные расстояния d_H (d/n) с табличными значениями и определить их индексы.

Индицирование не всегда однозначно, так как нескольким совокупностям индексов H_i в общем случае могут отвечать совпадающие или неразличимые в пределах точности измерений значения d_H.

Поэтому более достоверное и однозначное индицирование можно осуществить, сопоставляя экспериментальные и табличные значения d_H и j_HH`. Индексы плоскости обратной решетки, изображенной на электронограмме (u₁u₂u₃), т.е. оси зоны отражающих плоскостей можно найти, зная индексы любой пары узлов H¹ и H² из соотношения (1).

Для высокосимметричных, особенно кубических кристаллов, существует несколько сочетаний индексов H_j, которым соответствует одно и тоже значение d_H и j_{HH`</sub>. Полученные индексы оси зоны определяют один из вариантов, правильно характеризующих ориентировку кристалла. Остальные столь же правильные ориентировки можно получить из уравнения (1) перестановкой и изменением знаков индексов H<sub>j</sub><sup>1</sup> и H<sub>j</sub><sup>2</sup>, сохраняющих те же значения d<sub>H</sub>и j<sub>HH`}. Если ось зоны является в кристалле осью симметрии четвертого порядка, то индицирование одной плоскости обратной решетки (являющейся плоскостью симметрии) позволяет однозначно определить ориентировку кристалла. Если же этого нет, то для однозначного определения ориентировки необходимо привлекать данные об отражении от плоскостей других, не входящих в данную нулевую зону плоскостей. Отражения от этих плоскостей часто имеются на той же электронограмме.

Рассмотрим теперь рефлексы, принадлежащие последующим Лауэ-зонам. Для каждого узла, лежащего в одной из плоскостей, параллельных плоскости (u₁u₂u₃), справедливо соотношение:

 (2)

где N - целое число.

Для последовательно расположенных плоскостей ряд значений N определенный. Так, для ГЦК решетки [u₁u₂u₃]=[111] N=0,1,2,3…, а для [u₁u₂u₃]=[110] N=0,2,4… При заданном направлении [u_j] значения N легко получить из уравнения (2), если учесть, что индексы H_jⁱ должны удовлетворять правилам погасания, определяемыми пространственной группой решетки кристалла. Индицирование рефлексов ненулевой Лауэ-зоны позволяет однозначно определить ориентировку кристалла. Плоскости обратной решетки тем ближе одна к другой, чем больше период идентичности вдоль направления [u_j]. В этом случае разделение рефлексов, принадлежащих разным Лауэ-зонам, на электронограмме не четкое. Наоборот Лауэ-зоны легче проявляются, если период идентичности вдоль направления [u_j] небольшой, а плоскости обратной решетки, перпендикулярные этому направлению, густо заполнены узлами. Это обычно бывает, если индексы U_j соответствуют важному направлению. Хорошо выраженные Лауэ-зоны получаются на электронограмме, если важное направление отклоняется на малый угол r от оси пучка. В этом случае рефлексы располагаются так, что центр электронограммы отклонен от следа важного направления на расстояние r. Тогда угол между пучком и этим направлением можно определить из уравнения:

где L – расстояние от образца до фотопластинки.

Определение угла r имеет важное значение, если электроннографически устанавливается ориентационная связь двух фаз.

Индицирование электронограмм кристалла с неизвестной структурой определяется набором на них осей и наименованием их. Для этого снимают несколько электронограмм. Анализ их симметрии и измерение большого числа межплоскостных расстояний и углов между векторами обратной решетки помогают определить ячейку обратной решетки. Желательно снимать электронограммы, содержащие ряды близко расположенных рефлексов, последние будут соответствовать важным направлениям в кристалле. Такие узловые направления в обратной решетке определяют семейство кристаллографических плоскостей с большими межплоскостными расстояниями. Это даст дополнительные указания относительно размеров элементарной ячейки кристалла и, следовательно, также поможет выбрать оси обратной решетки. Величину трансляций вдоль этих осей и углы между ними можно получить из нескольких электронограмм, снятых так, что углы между последовательными положениями кристалла известны. Именно сопоставление таких взаимосвязанных сечений обратной решетки позволяют установить трехмерную систему осей обратной решетки. В частности. Одним из методов построения трехмерной обратной решетки является метод вращения. Вращая кристалл вокруг оси пучка, выставляют какое-либо важное узловое направление (иногда это может быть просто одна из осей) параллельно оси наклона кристаллодержателя, перпендикулярной пучку электронов. После этого, поворачивая кристалл на известные углы вокруг этой оси, снимают несколько электронограмм, содержащих общее узловое направление. При этом обычно одна из электронограмм соответствует координатной плоскости обратной решетки. Направление третьей оси, не лежащей в этой плоскости, можно найти, построив трехмерную модель обратной решетки.

Определив таким образом направление осей обратной решетки и осевые трансляции, легко можем вычислить набор возможных ее векторов. Затем, используя эти векторы как базисные, найдем индексы всех отражений на электронограммах.

Пространственная группа исследуемого кристалла определяется по погасаниям, закон которых легко установить после индицирования электронограмм.

 

Кристаллографические данные, получаемые из анализа тонкой структуры электронограмм.

1. Определение ориентационных соотношений двух фаз является существенной частью электронно-микроскопических исследований фазовых превращений. Для установления ориентационных соотношений необходимо: а) проиндицировать картину дифракции от каждой фазы, однозначно установив оси зон и их взаимную ориентировку, так как может оказаться, что оси зон каждой фазы несколько отклонены от оси пучка; б) построить и наложить стереографические проекции двух фаз, соответствующим образом сориентировав их и учтя точность в определении осей зон; в) отметить положения плотноупакованных направлений и нормалей к плотноупакованным и другим плоскостям для каждой фазы.

В практике кристаллографического анализа ориентационных соотношений удобно формальное представление с помощью матрицы преобразований решеток α_ik. Воспользуемся найденными по электронограмме (или совокупности нескольких электронограмм, снятых после некоторых заданных поворотов образца) соотношениями между ориентировками обратных решеток исходной и сопрягающейся с ней любой фазы. Найдем положение осевых векторов ОР новой фазы Х_j^* в системе координат ОР исходной фазы Х_j^* = α_jk X_k^* (α_jk – матрица преобразования осей исходной решетки и новой фазы при заданном ориентационном соотношении). Матрица α_jk должна удовлетворять условию: V*^нф_яч :V*^иф_яч = |α_jk|, учитывающему различие объемов элементарных ячеек исходной ( V*^иф_яч ) и новой (v*^нф_яч) фаз. Это позволяет строить совмещенные сечения ОР, т.е. теоретические электронограммы для любой ориентировки исходной фазы.

 

2. Если в монокристаллической матрице содержатся включения частиц, форма которых вызывает сильное размытие узлов (см. рисунок ) соответствующей им обратной решетки, электронограмма содержит ряд характерных особенностей.

Узлы обратной решетки представляют собой стержни, длина которых обратно пропорциональна толщине пластинчатых включений. Дефекты упаковки в кристаллах с г.ц.к. решеткой создают области с гексагональной упаковкой, а в кристаллах с гексагональной решеткой – области с ГЦК структурой, толщиной в несколько атомных слоев. Такие области по форме эквивалентны тонким кристаллам. Тонкие упорядоченные домены (например, зоны Гинье-Престона), имеющие ту же структуру, что и матрица, также вызывают растяжение узлов обратной решетки. Включениям в виде иголок, правильно ориентированным в матрице, соответствуют узлы-диски.

В отличие от размытия узлов, обусловленного малой толщиной исследуемого образца и параллельного нормали к поверхности тонкой фольги, в данном случае ориентация размытых узлов может быть по отношению к поверхности фольги произвольной, зависящей от ориентации и формы частиц в матрице.

Рассмотрим пересечение узлов-стержней сферой Эвальда. Если размытие узлов перпендикулярно оси пучка, то на электронограмме появляются тяжи. Если они расположены под каким-то углом к оси пучка, - рефлексы на электронограмме будут или слегка смещаться из нормальных положений, или даже расщепляться на два или несколько рефлексов, Направление и величина смещения или расщепления рефлексов очень чувствительны к ориентировке образца, поскольку даже небольшие наклоны существенно изменяют положение точки пересечения стержня со сферой Эвальда (рисунок ).

Если сильно вытянутые стержни параллельны электронному пучку, то на электронограмме может появиться множество рефлексов, соответствующих узлам ненулевой Лауэ-зоны.

Аналогичные рассуждения можно провести для узлов, размытых в форме плоских дисков.

Следует отметить, что интенсивность тяжей на точечной электронограмме пропорциональна количеству и рассеивающей способности частиц, правильно ориентированных в матрице, создающих эффект формы.

3. Появление закономерно расположенных экстра-пятен в положениях, которым соответствуют простые дробные индексы в системе координат матрицы (предполагается, что электронограмма матрицы проиндицирована), может служить признаком присутствия в образце сдвойникованных кристаллов. В ортогональной системе координат поворот решетки на угол γ вокруг оси, направляющие косинусы которой ω_i (|ω|=1), преобразует любой вектор Н в соответствии с уравнением

Н_i¢ = М_ij Н_j, где матрица М_ij имеет вид:

где C = 1 – cosγ; k = cosγ; s = sinγ. В случае двойникования угол γ = π. Отсюда С = 2, k=-1, s = 0. Тогда

Рассмотрим пример. Пусть в кубическом ГЦК кристалле параллельно электронному лучу направление [1 2 3]. Пусть плоскость двойникования (111), тогда ω = (1/√3, 1/√3, 1/√3). После двойникования по плоскости (111) параллельно оси пучка устанавливается направление [321]. Что легко вычислить, используя матрицу М_ij. Теперь для совмещения ОР матрицы и двойника, необходимо взять какие-либо два узла плоскости (321)* ОР двойника, например `1 1 1 и `1`1 5. С помощью матрицы М<sub>ij</sub> можно вычислить их координаты в системе координат основного кристалла. Узел `111 будет иметь координаты , а узел 1`1 5 – соответственно 3 3`3 (см. рисунок ).

Практически, особенно для некубических кристаллов, плоскость обратной решетки (ОР) двойника, параллельная плоскости матрицы (т.е. электронограмме), может быть нерациональной.

В таких случаях необходимо построить модель обратной решетки матрицы и двойника, а затем установить, какие узлы обратной решетки двойника достаточно близко расположены к плоскости обратной решетки матрицы и могут попасть на электронограмму. При этом необходимо точное знание ориентировки кристалла и степени его совершенства, позволяющих оценить присутствие на электронограмме рефлексов, не лежащих точно в плоскости нулевой Лауэ-зоны.

4. Из-за больших сечений рассеяния атомов, отраженные пучки электронов имеют большую интенсивность. Поэтому необходимо учитывать эффекты многократного рассеяния даже в сравнительно с рентгеновскими лучами малых объемах. Двукратное отражение приводит к появлению на электронограммах рефлексов, отвечающих узлам обратной решетки с весовой функцией G = 0. Эти рефлексы должны были бы иметь нулевую интенсивность, так как структурная амплитуда для таких отражений равна нулю.

На рисунке показана схема двойного отражения. Оно возникает тогда, когда луч, отраженный от одного семейства плоскостей ( h_j¹), затем отражается от другого семейства ( h_j²) (соответствующие векторы обратной решетки (H₁и`H<sub>2</sub>). В результате на электронограмме появляется рефлекс Р<sub>3</sub>, находящийся на расстоянии H<sub>2</sub> от рефлекса Р<sub>1</sub> и H<sub>3</sub> от начала координат О. Вектор `H₃ также является вектором обратной решетки, так как `H₃ = H₁ + H₂ (Н_j⁽³⁾ = Н_j⁽¹⁾ ± Н_j⁽²⁾).

Если структурная амплитуда для отражения с индексами Н_j⁽³⁾ равна нулю, на электронограмме может появится рефлекс. Электронограммы с учетом двойной дифракции строятся трансляцией без вращения исходной электронограммы, содержащей рефлексы, разрешенные законом погасания, на векторы трансляции, определяющие координаты сильных отражений.

Если в структуре присутствуют две фазы и отражение может происходить последовательно сначала на решетке одной, а затем другой фазы, то в этом случае будут появляться эффекты двойной дифракции. Если фазы имеют определенное структурное соответствие, двойную дифракцию можно проиллюстрировать следующим образом. На рисунке показана схема электронограммы от матрицы и включения второй фазы. Если пучок Р₁ может вторично отразиться от решетки включения, то возникает рефлекс Q₁. Повторив рассуждения для всех отражений матрицы, получим электронограмму. Расстояние между рефлексами матрицы и двукратно отраженными рефлексами равно `r<sub>M</sub> -`r_B (`r<sub>M</sub>, `r_B – расстояние от начала координат на электронограмме до рефлексов матрицы и включения соответственно. Аналогичные эффекты могут возникать при наложении двух одинаковых кристаллов с малым относительным поворотом (рисунок ). Двукратное отражение может происходить не только при наличии включений в тонких фольгах при съемке электронограмм «на просвет» (чаще всего при электронно-микроскопическом исследовании), но и тогда, когда на матричном кристалле имеется поверхностный слой (ориентированный окисный слой) или когда два кристалла наложены один на другой, как это бывает при эпитаксии.

 

5. При дифракции электронов в «толстых» слоях (10‾⁵ см) относительно совершенных кристаллов на электронограмме возникают пары параллельных темных и светлых линий, называемых кикучи-линиями. Кикучи-линии можно использовать для определения ориентировки кристалла, Лауэ-симетрии, параметров решетки и параметра отклонения от точного брегговского положения (`s ). При исследовании поверхности массивных кристаллов, появление кикучи-линий на электронограмме может служить признаком относительного совершенства их структуры. «Резкость» линий зависит от строгой параллельности отражающих плоскостей. Даже при небольшой «расстройке» параллельности (порядка минут) кикучи-линии становятся размытыми. Так при послойном стравливании нарушенного слоя подложек для эпитаксиального наращивания по постепенному повышению остроты и четкости кукучи- линий легко установит момент, когда нарушенный слой полностью удален.

Строгое описание интенсивности и геометрии кикучи-линий можно дать в рамках динамической теории рассеяния. Однако качественное понимание эффекта можно получить, воспользовавшись следующей упрощенной схемой.

Пусть часть некогерентно рассеянных электронов с энергией, очень близкой к энергии падающих на кристалл электронов, распространяется от места соударения пучка с кристаллом так, как если бы непосредственно под поверхностью кристалла находился источник электронов. Угловое распределение интенсивности электронов, выходящих из источника, таково, что в направлении первичного пучка она максимальна и монотонно убывает с увеличением угла рассеяния. Эти электроны могут также отражаться от плоскостей решетки под брегговскими углами. На рис. линии ОА и ОВ изображают пути таких электронов, отражающихся в направлениях К₁и К₂. Каждый из отраженных пучков лежит на поверхности конуса с осью, перпендикулярной отражающим плоскостям, и углом полураствора (90-θ). Эти конусы пересекают фотопластинку по гиперболам очень маленькой кривизны (на пластинке – практически прямые линии). Так как пучок АВ интенсивнее, чем ОА, то отраженная суммарная интенсивность в направлении К₂ больше, чем в направлении К₁ . В результате фон на электронограмме в направлении К₁ будет слабее среднего, а в направлении К₂ сильнее, что и соответствует на экране светлой и темной линиям.

Очевидно, что симметрия расположения кикучи-линий соответствует симметрии кристалла относительно оси первичного пучка. Расстояние между светлой и темной линиями удовлетворяет соотношению:

 

С = λL = R d_H cos²φ (3)

 

где R- расстояние между темной и светлой кикучи-линиями;

φ – угол между первичным электронным пучком и плоскостями с межплоскостным расстоянием d_H .

 

Соотношение (3) может быть использовано для определения набора значений d/n при идентификации фазы. Найдя по расстоянию между двумя парами линий величины и , можем определить ось зоны, в которую входят эти две системы плоскостей, ее отклонение от оси пучка (компоненты этого отклонения φ₁ и φ₂) и тем самым определить ориентировку кристалла. Легко понять, что при некотором малом изменении ориентировки кристалла, рефлексы на электронограмме практически не смещаются, изменяя лишь свою интенсивность. Но кикучи-линии смещаются так, как если бы они были жестко связаны с кристаллом, поэтому направление и величина их смещения с высокой точностью отвечают изменению ориентировки кристалла. Вектор, характеризующий отклонение `s для данного семейства плоскостей можно найти по расположению кикучи-линий, связанных с ним. Если кристалл ориентирован так, что плоскости (Н_j ) находятся точно в брегговском положении, т.е. |s| = 0, то темная линия на электронограмме проходит через рефлекс Н_j, а светлая – через след первичного пучка.

Если вектор s не равен нулю, то темная кикучи-линия проходит на некотором расстоянии Δr_H от соответствующего рефлекса. Величину параметра s можно найти из соотношения :

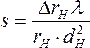 (4)

 

где Δr_H - расстояние на электронограмме от темной кикучи-линии до соответствующего рефлекса, положение которого задается радиусом-вектором r_H.

Очевидно, что вектор r_H перпендикулярен кикучи-линиям. Знак положительный, если кикучи-линия проходит от центра дальше рефлекса и отрицательный, если – ближе. При |s|>0 угол скольжения первичного пучка больше брегговского, при |s|<0 меньше.

 

6. В связи с особой ролью поверхности в технологии современной микроэлектроники остановимся на некоторых возможностях изучения качества микроповерхности на основе использования быстрых электронов в скользящей схеме отражения от поверхности. Картины дифракции от гладкой поверхности формируют слои порядка долей нанометра. Это очевидно, если учесть, что при реальной траектории пучка электронов в кристалле порядка десятков нанометров при угле скольжения порядка 1 – 3⁰ глубина проникновения пучка составляет десятые доли нанометра. Для шероховатой поверхности чувствительность к обнаружению слоев понижается.

У исследователей процессов молекулярно-лучевой эпитаксии атомарный рельеф поверхности подложек вызывает особый интерес.

При дифракции именно от гладкой поверхности, а не на выступах микрорельефа, в формировании дифракционной картины принимают участие практически атомы верхнего двумерного слоя. Обратная решетка такой двумерной сетки представляется совокупностью бесконечных стержней, перпендикулярных поверхности. Очевидно, что на перпендикулярном стержням сечении узлы нумеруют только двумя индексами. Стержень, проходящий через начало координат имеет индексы 00, а индексы задают положение любого узла в трансляциях перпендикулярного сечения (см. ниже). Электронограмма в скользящей схеме отражения будет иметь вид, показанный на рисунок . Однако, если поверхность представляет собой не плоскость, а совокупность атомарных ступеней, расположенных регулярно или хаотически, то на дифракционную картину от плоской сетки накладывается модуляция, зависящая от формы, размеров и степени регулярности или хаотичности ступеней. Проиллюстрируем это на простейшем, но важном примере.

Положим, что какая- либо плотноупакованная плоскость отклонена на угол α от поверхности кристалла. Если угол α мал – такая грань называется вицинальной. Ее поверхность можно представить в виде ряда ступеней-террас, параллельных какому-либо узловому направлению с малым периодом идентичности (рисунок ). В частном случае регулярного ряда ступеней суммарную обратную решетку, являющуюся образом условий отражения, можно представить следующим образом. ОР атомной рассеивающей сетки поверхности террасы-стержни, перпендикулярные ее поверхности. Они очень тонкие в направлении вдоль террасы и могут иметь конечную ширину в направлении малого размера террасы. Сечение обратной решетки новой периодичности (см. рисунок ) – краев регулярного ряда террас – так же стержни перпендикулярные поверхности, составляющие с предыдущими стержнями угол α. Расстояние между стержнями позволяет найти ширину террасы. По углу α между стержнями можно оценить и высоту (h=D^.sinα). Если ступеньки нерегулярные (D≠const), то вторые стержни размываются. Степень их размытия может быть качественной характеристикой регулярности ступеней.

Использование быстрых электронов по сравнению с медленными (см. ниже) имеет иногда преимущество, состоящее в возможности получения электронограмм в процессе наращивания слоев, например методом молекулярно-лучевой эпитаксии.

При отражении электронного пучка от гладкой поверхности становится заметным преломление электронных волн на границе раздела двух сред.

Проникая в кристалл, электроны под действием внутреннего потенциала решетки меняют свою энергию, соответственно меняется и длина волны. Коэффициент преломления μ связан со средним внутренним потенциалом Ф соотношением:

где U – ускоряющий потенциал.

Угол скольжения φ пучка по поверхности кристалла и брегговский угол θ удовлетворяют уравнению

или

Очевидно, что отраженный луч только тогда выйдет из кристалла, если sin²φ > 0. Поэтому, если выявляется картина трехмерной дифракции при не слишком малых φ, иногда отражения от плоскостей с достаточно большими межплоскостными расстояниями могут отсутствовать на электронограмме. Кроме того, следствием преломления является сдвиг всей электронограммы в сторону тени образца по сравнению с электронограммой, снятой «на просвет», когда преломление практически не проявляется.

/var/www/studfiles2/data/www/download/2706/299/MzSEcjmZA7.H74k