
Новая папка / Лекция №06 Движение электрона в электрическом поле
.docxЛекция № 6
Движение электрона в электрическом поле
Электронная оптика занимается задачами
-
формирования,
-
фокусировки
-
отклонения
электронных пучков с помощью
-
электрических и
-
магнитных полей.
Ее физической основой является аналогия между
-
законами распространения света и
-
движением заряженных частиц, в том числе и электронов,
в электрических и магнитных полях.
Эта оптико-механическая аналогия позволяет подойти к задаче о траектории движения электрона
-
как c механической, корпускулярной, точки зрения, когда электрон рассматривается как частица,
-
так и с оптической, волновой, позиции, когда учитываются волновые свойства электрона.
В первом случае (корпускулярный подход) задача нахождения траектории электрона решается на основе использования второго закона Ньютона:
 (1)
(1)
 ;
;
 (2)
(2)
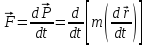 (3)
(3)
-
где
 —
сила, действующая со стороны поля на
электрон;
—
сила, действующая со стороны поля на
электрон; -
 —
скорость электрона;
—
скорость электрона;
-
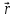 —радиус-вектор
электрона, характеризующий его положение
в пространстве в момент времени t
относительно
некоторого начала координат..
—радиус-вектор
электрона, характеризующий его положение
в пространстве в момент времени t
относительно
некоторого начала координат..
Если
сила
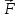 известна,
то можно, решив уравнение (3), найти
зависимость радиуса-вектора
известна,
то можно, решив уравнение (3), найти
зависимость радиуса-вектора
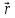 от
времени и тем самым установить траекторию
движения электрона. Однако точное
интегрирование этого уравнения возможно
лишь для случая весьма простых полей,
в частности, однородных электрических
и магнитных. В более сложных случаях
приходится прибегать к приближенным
методам решения этого уравнения.
от
времени и тем самым установить траекторию
движения электрона. Однако точное
интегрирование этого уравнения возможно
лишь для случая весьма простых полей,
в частности, однородных электрических
и магнитных. В более сложных случаях
приходится прибегать к приближенным
методам решения этого уравнения.
При волновом подходе к задаче движения электрона используется аналогия с принципам Ферма в оптике, утверждающем, что из всех возможных траекторий между двумя точками А и В световой луч распространяется по той, которая имеет наименьшую оптическую длину, так что
 (4)
(4)
где:
n — показатель преломления;
dl.— элемент траектории светового луча.
Как в световой, так и в электронной оптике из принципа Ферма следует основной закон геометрической оптики — закон преломления.
-
Электрическое поле (в отличие от магнитного) вызывает изменение величины скорости электрона (включая ее направление).
-
Магнитное поле приводит только к изменению направления скорости электрона.
Для стационарного поля сумма потенциальной и кинетической энергии движущегося в этом поле электрона является величиной постоянной
 (5)
(5)
Если

то

Потенциальная энергия электрона в электростатическом поле в точке, характеризуемой потенциалом φ, равна Епот = – eφ
Выберем на траектории электрона две точки, из которых одна произвольная, а вторая лежит на катоде, эмиттирующем электроны.
У электрона на поверхности катода (x=0) энергия слагается из
-
потенциальной -еφ0 и
-
кинетической

составляющих.
У
электрона, находящегося на
расстоянии
X
от катода энергия также слагается из
потенциальной
-еφ1
и кинетической
 составляющих.
составляющих.
Тогда на основании формулы (2) можно написать, что
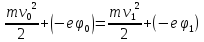 (6)
(6)
затем
 (7)
(7)
Примем
во внимание, что на катоде скорость
электрона
 значительно
меньше скорости
значительно
меньше скорости
 ,
а потому может быть приравнена нулю,
как и потенциал φ0
на поверхности катода также равен нулю.
,
а потому может быть приравнена нулю,
как и потенциал φ0
на поверхности катода также равен нулю.
Тогда
 ,
,
Т.е.

φ1=
U,
и тогда
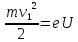 (8)
(8)
где U — разность потенциалов, пройденная электроном на траектории своего движения.
Поскольку, проходя разность потенциалов U, электрон приобретает скорость V1, т. е. ускоряется, величина U носит название ускоряющего напряжения.
Если U< 0, то при движении по траектории электрон будет терять свою скорость и U будет являться напряжением замедляющим.
Уравнение
(3) дает возможность выражать энергию
электрона и его скорость через разность
потенциалов
U,
которую
должен пройти первоначально покоившийся
электрон, чтобы приобрести скорость V
или
соответствующую ей кинетическую энергию
 .
.
Единица измерения кинетической энергии электрона:
1 электронвольт = 1,6•10-12 эрг = 1,6•10-19 дж
