13

1.2 Диференційний переріз розсіяння електронів на атомі

При непружному характері розсіювання характерна зміна хвильового вектора електрона не тільки за напрямом, а й за величиною. При цьому частина енергії електрона передається атому мішені (зразка), внаслідок чого він переходить у збуджений або іонізований стан.

Диференційний переріз непружного розсіяння електронів можна представити у вигляді:

, (1.17)

де К та К_n – хвильові числа електрона до і після зіштовхування з атомом n; та - одиничні вектори у напрямку падаючого та розсіяного електронів; U_0n – матричний елемент.

Математичний запис для матричного елемента U_0n має вигляд:

. (1.18)

Для визначення загального диференційного перерізу необхідно повністю скласти (1.17) по всім можливим станам, тобто:

. (1.19)

Диференційний переріз непружно розсіяних електронів також можна представити виразом:

, (1.20)

де

нм, (1.21)

S – фуекція некогерентного розсіяння, яка залежить від атомного фактора F і матричного елемента V_0n.

Під час взаємодії з твердим тілом електрони втрачають деяку кількість енергії, характерну для даної речовини. Це – характеристичні втрати. Механізм втрат енергіїелектронів при взаємодії з ізольованими атомами зводиться до їх іонізації та збудження. У твердому тілі, коли атоми не ізольовані, при взаємодії з електронами спостерігається два процеси: 1) збудження коливань валентних електронів атомів (плазмові коливання); 2) парноелектронні взаємодії.

Частота плазмових коливань складає:

, (1.22)

енергія плазмона

, (1.23)

де n – концентрація електронів; ħ=h/2 - постійна Планка.

Повний ефективний переріз процесу колективного збудження складає:

, (1.24)

де Е_р – величина характеристичних втрат електрона; Е₀ – початкова енергія електрона; r – середня відстань між електронами, яка пов’язана з їхньою концентрацією n співвідношенням:

, (1.25)

де А – атомна вага;  - густина; z – валентність.

Електрон твердого тіла внаслідок непружної взаємодії з падаючим швидким електроном переходить з одного енергетичного стану в інший. Енергія, що виділяється при міжвузельних переходах, визначається за формулою:

. (1.26)

Розглянемо випадок пружного розсіяння електронів на атомі. Нехай електронний потік рухається на атом вздовж осі OZ із швидкістю . Цей потік можна описати плоскою хвилею . Розсіяна хвиля описується виразом:

, (1.27)

де - хвильовий вектор; - радіус-вектор; f() – атомна амплітуда розсіяння.

Знаючи величину f(), можна визначити число електронів, розсіяних за одиницю часу всередині тілесного кута d, тобто диференційний переріз розсіяння D(). Нижче, для пояснення, наведено рисунок 4.4.

Рисунок 1.4 – До визначеннядиференційного перерізу розсіяння D()

Інтенсивність розсіяного електронного пучка, який проходить за одиницю часу крізь елемент поверхні dS у точці з координатами (r,), має вигляд:

. (1.28)

Число електронів, розсіяних за одиницю часу всередині тілесного кута d, дорівнюватиме:

, (1.29)

звідки

, (1.30)

де

, (1.31)

є атомною амплітудою розсіяння; U(r)=-(ze²/r)(z_p/z) – атомний потенціал, а величина z_p/z – враховує вплив екранування електронів.

Диференційний переріз розсіяння на один атом визначається співвідношенням:

. (1.32)

Використовуючи функцію радіального розподілу атомів (r), яка визначає число атомів dN, розміщених на відстані r від деякого початкового атома так, що dN=4r(r)dr, рівняння (1.28) можна представити у вигляді:

(1.33)

де - параметр розсіяння; ₀ – середнє число атомів на одиницю об’єму; r_max – розмір мікрокристала в об’єкті.

Тоді для диференційного перерізу маємо:

, (1.34)

де f²(s) – некогерентна частина пружного розсіяння, та:

. (1.35)

Другий і третій доданки в дужках рівняння (1.33) являють собою інтерференційні члени, що залежать від розміру кристалітів. При великому r (r) ₀ та S_p0. При r0 S_p та S₀ обидва наближаються до нуля.

Вид типових функцій радіального розподілу атомів (ФРРА), отриманих за результатами електронографічного аналізу реальних аморфних сплавів наведено на рис. 4.5.

Рисунок 1.5 – функції радіального розподілу атомів для аморфних сплавів Fe₂₂Ni₇₀Si₄B₄ (1) та Fe₇₀Ni₂₂Si₄B₄ (2)

Величина, що визначає зв’язок між просторовим розміщенням атомів та дифракційною картиною, називається структурним фактором. Він являє собою (рис. 1.6) суму амплітуд розсіяння усіх атомів об’єкта з урахуванням їх фаз.

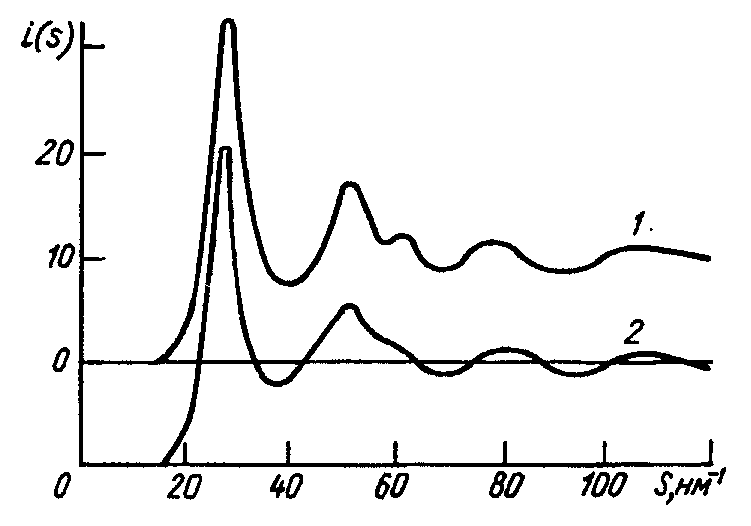
Рисунок 1.6 – Структурний фактор i(s) сплаву Fe₂₂Ni₇₀Si₄B₄ для аморфного (1) та рідкого (2, при 1400 К) станів

Якщо структурний фактор відомий, то можливо передбачити дифракційну картину та визначити середні міжатомні відстані і координаційні числа <z>. Структурні фактори поділяють на кінематичний, що визначає однократне пружне розсіяння, та динамічний, що визначає багатократне та непружне розсіяння.

Таким чином, пружне та непружне розсіяння електронів мають різне кутове розділення. Тому залежність ефективних перерізів від апертурного кута об’єктивної лінзи електронного мікроскопа виявляється різною. Це означає, що частина пружного та непружного розсіяння, яка поглинається апертурною діафрагмою та визначає контраст зображення, змінюватиметься із зміною ₀.

Роль непружного розсіяння в утворенні амплітудного контрасту для різних атомів різна. При дослідженні об’єктів співрозмірних з міжатомними відстанями, які відрізняються високим ступенем впорядкованості своєї будови, треба враховувати дифракційні явища, пов’язані з хвильовою будовою електрона.