
Практикум2013
.pdf
Розділ 2. Інтегральне числення функцій кількох змінних |
21 |
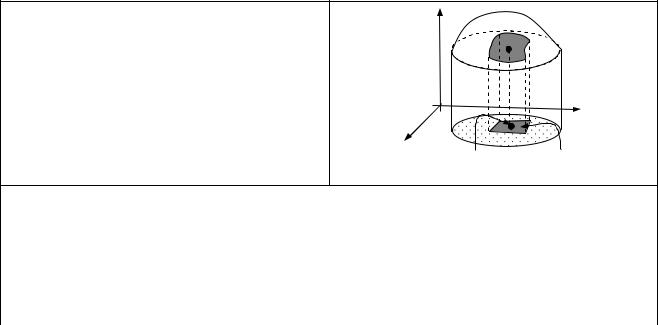
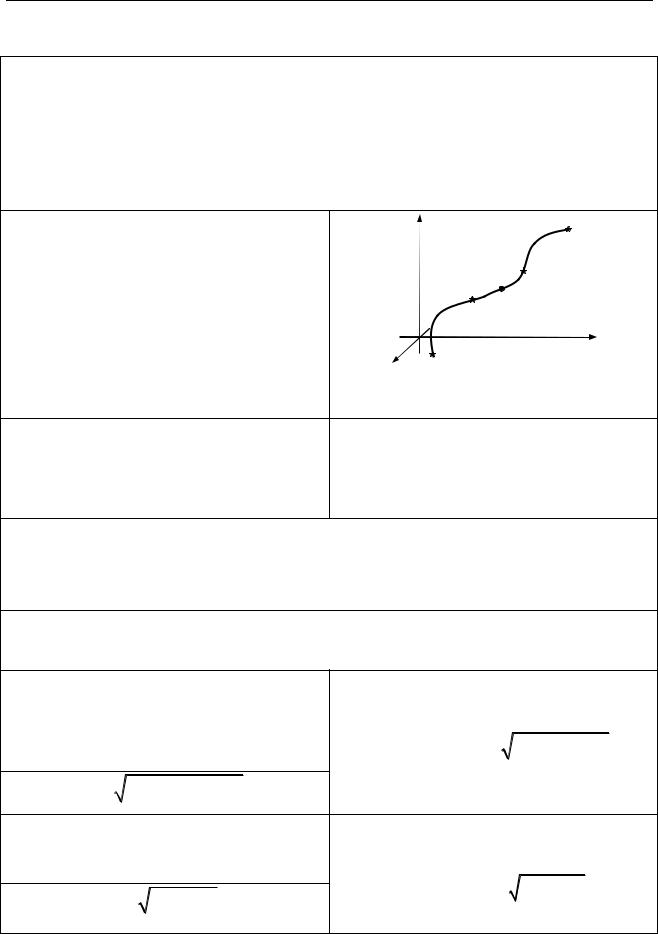
2.5. Невластиві інтеграли
Невластивий інтеграл 1-го роду |
Невластивий інтеграл 2-го роду |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
b |
|
b |
|
|
|
f(x)dx lim |
|
f (x)dx, |
|
|
f(x)dx lim |
|
f (x)dx, |
|
A |
|
|
0 |
|
||||
|
a |
|
a |
|
|
a |
|
a |
|
f — неперервна на кожному [a; A] |
a — точка нескінченного розриву, |
||||||||
|
|
|
|
|
f C(a;b] |
|
|
||
Якщо існує скінчена границя , то інтеграл збігається, якщо ж ні, то — інтеграл
розбігається.
Ознака порівняння. Якщо на |
Ознака порівняння. Якщо на |
||||||||
проміжку [a; ) функції f (x) та |
проміжку (a;b] функції f (x) та (x) |
||||||||
(x) неперервні і справджують умову |
неперервні, мають нескінченний розрив |
||||||||
0 f (x) (x) , то зі збіжності |
у точці x a і справджують умову |
||||||||
0 f (x) (x), то зі збіжності |
|||||||||
|
|
|
|||||||
|
|
|
b |
|
|
|
|
|
|
(x)dx випливає збіжність |
|
|
|
|
|
||||
(x)dx випливає збіжність |
|||||||||
a |
|
|
|||||||
|
|
|
a |
|
|
|
|
|
|
|
b |
|
|
|
|
b |
|||
f (x)dx, а з розбіжності f (x)dx |
|
|
|
|
|||||
f (x)dx, а з розбіжності f (x)dx |
|||||||||
a |
|
a |
|||||||
|
|
|
a |
|
|
|
|
a |
|
|
|
|
|
|
|
b |
|
||
випливає розбіжність (x)dx. |
|
|
|
|
|
||||
випливає розбіжність |
|
(x)dx. |
|||||||
|
|
a |
|
|
|
|
|
||
|
|
|
|
|
|
a |
|
||
|
|
|
|
|
|
|
|
||
|
|
||||||||
Гранична ознака порівняння. |
Гранична ознака порівняння. |
||||||||
Якщо на проміжку [a; ) функції |
Якщо на проміжку (a;b] функції f (x) та |
||||||||
f (x) та (x) додатні і неперервні, |
(x) додатні і неперервні, мають |
||||||||
існує скінченна |
|
|
нескінченний розрив у точці x a, |
||||||
lim |
f(x) |
A 0, |
існує скінченна |
|
|
|
|||
|
|
|
|
|
|
||||
|
|
f(x) |
|
|
|
||||
x |
(x) |
lim |
A |
0, |
|||||
|
|
|
|
|
|||||
|
|
|
(x) |
||||||
|
|
x a |
|
|
|
||||
|
|
|
|
|
|
||||
то f (x)dx та (x)dx |
b |
b |
|
|
|
||||
|
|
|
|
|
|
||||
a |
a |
то f (x)dx та (x)dx |
|
||||||
або одночасно збігаються, |
a |
a |
|
|
|
||||
або одночасно розбігаються. |
або одночасно збігаються, |
||||||||
|
|
|
або одночасно розбігаються. |
||||||
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
Розділ 2. Інтегральне числення функцій кількох змінних |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|||||
|
Якщо |
|
|
f (x) |
|
dx |
збігається, то |
Якщо збігається |
|
f (x) |
|
dx, то |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
||
|
збігається й |
|
f (x)dx. |
|
|
|
|
збігається й f (x)dx. |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, |
|
|
b |
|
dx |
|
|
|
|
|
|
|
|
|
1, |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
dx |
|
збігається, |
|
|
|
|
|
|
збігається, |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||||||||
|
|
|
|
|
|
|
|
1 |
(x a) |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
x |
|
розбігається, |
|
|
|
розбігається, |
|
||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
b |
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
b |
|
|
|
|
|
b |
|
|
|
|
|
|
|
|||
|
|
|
|
f(x)dx lim |
|
f (x)dx; |
|
|
f(x)dx lim |
|
f(x)dx; |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
a |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
b |
|
|
|
c |
|
|
|
b |
|
|
|
|
|||||
|
|
|
f (x)dx f (x)dx f (x)dx |
|
|
f (x)dx f (x)dx f (x)dx, |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
a |
|
|
|
a |
|
|
|
c |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c (a;b), |
lim f (x) |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x c |
|
|
|
|
|
|
|
||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
Головне значення (за Коші) |
Головне значення (за Коші) |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
b |
|
|
|
|
c |
|
|
|
b |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v.p. |
|
f (x)dx |
lim |
|
|
|
fdx |
|
fdx |
|
|
|||||
|
v.p. |
|
f (x)dx lim |
|
|
|
|
f(x)dx |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
a |
|
|
|
c |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.6. Подвійні інтеграли
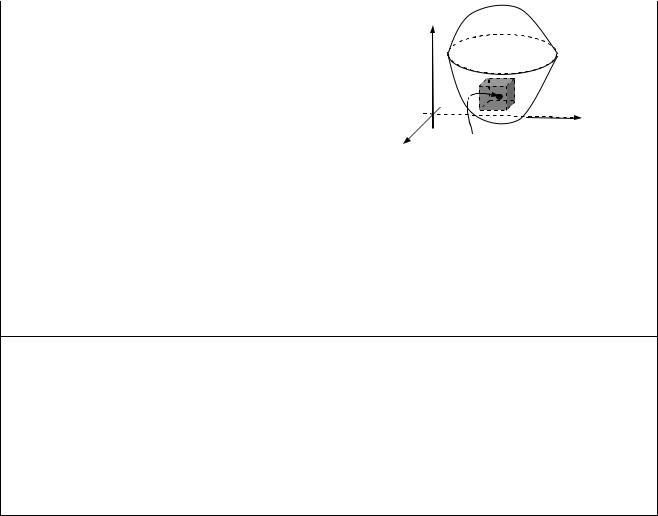
Подвійний інтеграл від функції f (x, y) за областю D
f (x, y)dxdy
D
n
lim f ( i, i ) Si,
maxn di 0 i 1
z
G
O |
y |
|
D |
||
|
||
x |
|
Mi ( i ; i ) Si
де Si — площі елементарних ділянок; di |
— їхні діаметри. |
|
|
|
|
Геометричний зміст подвійного |
|
|
інтеграла. Об’єм циліндричного тіла |
|
f (x, y)dxdy V |
G обмеженого зверху поверхнею |
|
|
z f (x, y) 0 |
|
D |
|
|
|
|
|
|
Розділ 2. Інтегральне числення функцій кількох змінних |
23 |
Основні властивості подвійного інтеграла
1)1 dxdy S(D) (площа D);
D
2) |
( f (x, y) g(x, y))dxdy f (x, y)dxdy g(x, y)dxdy |
|
|||||
|
D |
|
|
D |
|
D |
|
(лінійність); |
|
|
|
|
|
|
|
3) |
f (x, y)dxdy f (x, y)dxdy f (x, y)dxdy (адитивність); |
|
|||||
|
D1 D2 |
|
D1 |
D2 |
|
|
|
4) mS(D) |
f (x, y)dxdy MS(D), де m |
(x;y) D |
(x;y) D |
|
|||
|
min |
f (x, y), M max |
f(x, y) |
||||
D
2.7. Обчислення подвійних інтегралів
Перехід до повторних інтегралів у декартових координатах
Область |
y y 2(x) |
|
|
Пряма x (a b) перетинає |
||||||||||||||||
правильна в |
|
|
|
|
|
|
|
|
|
|
|
межу області не більше ніж у двох |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
напрямі осі Oy |
|
|
|
|
|
|
|
|
|
|
|
точках. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b 2(x) |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
y 1(x) |
|
f (x, y)dxdy dx |
|
f (x, y)dy |
|||||||||||
|
O a b |
x |
|
|
|
|||||||||||||||
|
D |
|
a |
1(x) |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Область |
y |
|
|
|
|
|
|
Пряма y (c d) перетинає |
||||||||||||
x (y) |
|
|
||||||||||||||||||
правильна в |
d |
|
|
1 |
|
|
|
|
|
|
|
межу області не більше ніж у двох |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
напрямі осі Ox |
|
|
|
|
|
|
|
|
|
|
|
точках. |
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
d 2(y) |
f (x, y)dx |
|||||
|
|
|
|
|
|
|
|
x 2(y) |
f (x, y)dxdy dy |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
O |
|
|
|
|
|
|
|
|
x |
D |
|
c |
1(y) |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Заміна змінних у подвійному інтегралі |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
Перехід до нових координат |
|
|
|
|
f (x, y)dxdy |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
x x(u, v), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x(u, v), y(u, v)) |
|
J(u, v) |
|
dudv |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
y y(u, v) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
з якобіаном J(u, v) |
|
u |
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
u |
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
24 |
|
|
|
|
Розділ 2. Інтегральне числення функцій кількох змінних |
|
|||||
|
|
|
|
|
|
|
|
|
||||
|
Перехід до полярних координат |
|
|
f (x, y)dxdy |
|
|||||||
|
|
|
cos , |
|
|
D |
|
|||||
|
x |
|
|
|
|
|||||||
|
|
|
|
|
|
f( cos , sin ) d d |
|
|||||
|
|
|
sin , |
|
|
|||||||
|
y |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
D |
|
||
|
|
|
J |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
|
Перехід до узагальнених полярних |
|
|
f (x, y)dxdy |
|
|||||||
|
координат |
|
|
|
|
|
D |
|
||||
|
x a cos , |
|
f (a cos ,b sin )ab d d |
|
||||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||
|
|
b sin , |
|
D |
|
|
||||||
|
y |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
J |
|
ab |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
|
Перехід до повторних інтегралів у полярних координатах |
|
||||||||||
|
|
|
|
|||||||||
|
Криволінійний сектор («радіальна |
Будь-який промінь |
|
|||||||||
|
область») |
|
|
|
( ) перетинає межу області |
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
|
2( ) |
не більше ніж у двох точках. |
|
|
f( , ) d d |
||
|
|
||
|
|
|
|
1( ) |
D |
|
|
|
|
2 ( ) |
|
O |
P |
d f ( , ) d . |
|
|
|
|
1( ) |
Криволінійний сектор |
|
|
|
охоплює початок координат
|
|
|
( ) |
|
|
( ) |
|
O |
|
P |
f( , ) d d d f ( , ) d |
||
|
|
|||||
|
|
|||||
|
|
|
|
0 |
||
|
|
|
|
D |
||
|
|
|
|
|
|
|
2.8. Застосування подвійних інтегралів |
|
|
||||
|
|
|
|
|
||
Площа плоскої області |
|
S(D) dxdy |
||||
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
Маса пластинки у формі області |
|
m (x, y)dxdy |
||||
|
|
|
||||
D з густиною (x, y) |
|
D |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Розділ 2. Інтегральне числення функцій кількох змінних |
|
|
25 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Статичні моменти пластинки |
|
Mx |
y (x, y)dxdy, |
|
|
|||||||||||||
|
щодо осей |
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
My |
x (x, y)dxdy |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Координати центра мас |
|
xc |
|
|
My |
|
, yc |
|
Mx |
|
|
|||||||
|
пластинки |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
m |
|
m |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||||||
|
Моменти інерції пластинки |
|
Ix |
y2 (x, y)dxdy, |
|
|
|||||||||||||
|
щодо осей |
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Iy |
x2 (x, y)dxdy |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Моменти інерції пластинки |
IO |
(x |
2 |
y |
2 |
) (x, y)dxdy |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
щодо початку координат |
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2.9. Потрійні інтеграли |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Потрійний інтеграл від функції |
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
u f (x, y, z) за областю G |
|
|
|
|
|
|
|
|
|
|
G |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
f(x, y, z)dxdydz |
|
|
|
|
|
|
|
|
|
|
Vi |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
G |
n |
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
lim |
f ( i, i, i ) Vi, |
|
x |
|
|
|
M ( ; |
; ) |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
max di 0 i 1 |
|
|
|
|
|
|
|
i |
|
|
i i |
i |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
де Vi |
— об’єми елементарних областей; di — їхні діаметри. |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Геометричний зміст потрійного |
|
(x, y, z)dxdydz m(G) |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
інтеграла. Маса тіла G з густиною |
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
(x, y, z) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Основні властивості потрійного інтеграла
1)1dxdydz V(G) (об’єм G);
G
2)лінійність;
3)адитивність
|
26 |
|
|
|
|
Розділ 2. Інтегральне числення функцій кількох змінних |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Обчислення потрійних інтегралів |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Область |
|
|
|
|
|
|
z |
|
|
2 |
Будь-яка вертикальна пряма перетинає |
|
|||||||||||||
|
циліндрична в |
|
|
|
|
|
|
|
|
|
|
межу області не більше ніж у двох |
|
|||||||||||||
|
напрямі осі Oz |
|
|
|
|
|
|
|
|
|
|
точках. |
|
|
|
|
|
|
|
|
|
|||||
|
2 |
: z z2(x, y), |
|
|
O |
|
|
|
|
|
f(x, y, z)dxdydz |
|
||||||||||||||
|
1 : z z1(x, y) |
|
|
|
|
1 y |
|
|
|
G |
|
|
|
|
z2 (x,y) |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
D |
|
|
|
dxdy |
dz |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
DOxy |
|
z1(x,y) |
|
||
|
Область циліндрична в напрямі |
|
|
f (x, y, z)dxdydz |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
осі Oz; проекція DOxy |
правильна у |
|
|
b |
G |
y2 (x) |
z2(x,y) |
|
|||||||||||||||||
|
напрямі осі Oy : |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
dx dy f (x, y, z)dz |
|
||||||||||||||||||
|
|
|
|
|
|
|
a x b, |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
y1(x) |
z1(x,y) |
|
||||||||||
|
|
D |
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
(x) |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Oxy |
|
y (x) y y |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Перехід до циліндричних |
|
|
|
|
|
f (x, y, z)dxdydz |
|
||||||||||||||||||
|
координат |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
f ( , , z) d d dz, |
|
|||||
|
x cos , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
sin , |
|
|
J |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
y |
|
|
|
|
|
|
|
|
, z) f ( cos , sin , z) |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( , |
|
|||||||||
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Перехід до узагальнених |
|
|
|
|
|
f(x, y, z)dxdydz |
|
||||||||||||||||||
|
циліндричних координат |
|
|
|
|
|
|
G |
|
f ( , , z)ab d d dz, |
|
|||||||||||||||
|
|
|
a cos , |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
b sin , |
|
J |
ab |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
y |
|
|
, z) f(a cos ,b sin , z) |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( , |
|
|||||||||
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Перехід до сферичних координат |
|
|
f (x, y, z)dxdydz |
|
|||||||||||||||||||||
|
|
r cos sin , |
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( , , r)r |
sin d d dr, |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||
|
|
r sin sin , |
J |
r |
sin |
|
|
|
|
|
|
|
|
|||||||||||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
r cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( , , r) |
|
||||
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(r cos sin , r sin sin , r cos ) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Розділ 2. Інтегральне числення функцій кількох змінних |
|
|
|
27 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Перехід до узагальнених |
|
|
|
|
|
|
f (x, y, z)dxdydz |
|
||||||||||||||||||||||
|
сферичних координат |
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
f ( , , r)abcr2 |
|
sin d d dr, |
|
||||||||||||||||||||||
|
x ar cos sin , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J |
|
abcr |
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
y br sin sin , |
|
|
|
|
|
|
|
|
|
|
|
f ( , , r) |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
f (ar cos sin ,br sin sin ,cr cos ) |
|
||||||||||||||||||||||||||
|
z cr cos |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2.10. Застосування потрійного інтеграла |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Об’єм тіла G |
|
|
|
|
|
|
V(G) |
dxdydz |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
Маса тіла з густиною (x, y, z) |
|
|
m(G) (x, y, z)dxdydz |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Статичні моменти тіла |
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
щодо координатних площин |
|
|
|
xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
y (x, y, z)dxdydz |
|
||||||||||||||||||||||||
|
|
|
|
M |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
xz |
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
yz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Координати центра мас тіла |
|
x |
|
Myz ;y |
|
Mxz ; z |
Mxy |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
c |
|
|
m |
|
|
c |
|
|
|
|
m |
|
|
|
c |
|
m |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Моменти інерції тіла |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
щодо координатних площин |
|
|
xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
I |
|
|
|
|
|
y |
|
|
(x, y, z)dxdydz |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
xz |
|
|
G |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
yz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Моменти інерції тіла |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
z |
2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
щодо осей координат |
|
|
Ox |
|
|
|
|
z |
2 |
dxdydz |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
I |
|
|
|
|
|
x |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
Oy |
|
|
G |
|
2 y2 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
Oz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Момент інерції тіла |
|
|
IO |
(x |
2 |
y |
2 |
z |
2 |
) dxdydz |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
щодо початку координат |
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
28 |
|
Розділ 2. Інтегральне числення функцій кількох змінних |
|
|
|
||||||||||||||
2.11. Криволінійні інтеграли 1-го роду |
|
|
|
|
|
|
|||||||||||||
Гладкі криві. Криву |
|
|
|
|
|
якщо функції x(t), y(t), z(t) — |
|||||||||||||
|
x(t), |
|
|
|
|
|
|
|
|
|
|
неперервно диференційовні. |
|
|
|||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(t), t |
[t ;t |
|
] |
|
|
|
|
Криву, що складається зі скінченної |
||||||||||
L : y |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
кількості гладких кривих і не має |
||||||
|
z(t), |
|
|
|
|
|
|
|
|
|
|
||||||||
z |
|
|
|
|
|
|
|
|
|
|
точок самоперетину, називають |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
називають гладкою, |
|
|
|
|
|
|
|
кусково-гладкою. |
|
|
|
||||||||
Криволінійний інтеграл 1-го роду |
z |
|
|
|
L |
|
|
||||||||||||
від функції f (x, y, z) уздовж кривої L |
|
|
|
li |
An |
|
|
||||||||||||
|
|
f (x, y, z)dl |
|
|
|
|
|
A |
|
|
|||||||||
|
|
|
|
|
|
|
|
i |
|
|
|||||||||
|
|
|
|
|
|
|
Mi( i; i; i ) |
||||||||||||
|
|
L |
|
|
|
|
|
|
|
|
|
|
O |
|
|||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
Ai 1 |
|
|
|
||
|
lim |
|
f ( , , ) l , |
|
|
A |
|
|
y |
||||||||||
|
max l 0 |
|
|
i |
|
i |
i |
i |
x |
|
|
|
|||||||
|
|
i |
i 1 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||
де li |
— довжина ланки Ai 1Ai . |
|
|
|
|
|
|
|
|
||||||||||
Фізичний зміст криволінійного |
(x, y, z)dl m(L) |
||||||||||||||||||
інтеграла 1-го роду. Маса, |
|
|
|||||||||||||||||
розподілена вздовж кривої L з |
|
L |
|
|
|
|
|
||||||||||||
густиною (x, y, z) 0 |
|
|
|
|
|
|
|
|
|||||||||||
Основні властивості криволінійного інтеграла 1-го роду |
|
|
|
||||||||||||||||
1) 1 dl |
l(L) (довжина L); 2) лінійність; 3) адитивність. |
|
|
|
|||||||||||||||
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обчислення криволінійного інтеграла 1-го роду |
|
|
|
|
|
|
|||||||||||||
(крива L — кусково-гладка) |
|
|
|
|
|
|
|
|
|||||||||||
|
|
x(t), |
|
|
|
|
|
|
|
|
|
|
|
|
f (x, y, z)dl |
|
|
||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
L : |
|
y(t), t [t ;t |
|
] |
|
|
|
|
|
|
|
|
|||||||
y |
2 |
|
|
t2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
z(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
2 |
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
f(x(t), y(t), z(t)) xt yt |
zt dt |
|||||
|
dl x |
2 y 2 z |
2dt |
|
t1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
t |
|
|
t |
|
|
t |
|
|
|
|
|
|
|
|
||
|
|
x(t), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
f (x, y)dl |
|
|
|
||
L : |
|
|
|
t [t ;t |
|
] |
|
|
|
|
|
|
|
||||||
|
y(t) |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
y |
|
|
|
|
1 |
|
2 |
|
|
|
t |
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dl |
|
x 2 |
y 2dt |
|
|
f (x(t), y(t)) xt2 yt2dt |
|||||||||||
|
|
|
|
t |
|
|
|
t |
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

Розділ 2. Інтегральне числення функцій кількох змінних |
29 |
L : y y(x), a x b |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
f (x, y)dl f (x, y(x)) 1 y 2dx |
|||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
dl |
|
1 y 2dx |
L |
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
L : ( ), |
|
|
|
|
|
|
f (x, y)dl |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dl |
2 2d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
||||||
|
|
|
f ( ( ) cos , ( ) sin ) |
d |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
2.12. Застосування криволінійного інтеграла 1-го роду |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Довжина дуги L |
|
|
|
|
|
|
|
|
l(L) |
|
dl |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Маса розподілена вздовж кривої |
|
|
m(L) (x, y, z)dl |
|
|
|
|
|
|||||||||||||||||||||||||
з густиною (x, y, z) |
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Статичні моменти кривої |
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
щодо координатних площини |
|
|
M |
|
|
|
|
|
|
|
|
|
|
(x, y, z)dl |
|||||||||||||||||||
|
|
|
|
y |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
xz |
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
yz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|||||||||||||||||||||||||||||
Координати центра мас |
x Myz ;y Mxz ; z Mxy |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
кривої |
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
m |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Моменти інерції кривої |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
щодо координатних площин |
|
|
I |
|
|
|
|
|
|
|
(x, y, z)dl |
||||||||||||||||||||||
|
|
|
|
y |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
xz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
yz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Моменти інерції кривої |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
z |
2 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||
щодо осей координат |
I |
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
x |
|
|
|
(x, y, z)dl |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
Ox |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
Oy |
|
|
|
|
|
|
|
2 y2 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
L x |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
Oz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Момент інерції кривої |
IO |
|
(x |
2 |
|
y |
2 |
|
z |
2 |
) (x, y, z)dl |
||||||||||||||||||||||
щодо початку координат |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 Розділ 2. Інтегральне числення функцій кількох змінних
2.13. Криволінійні інтеграли 2-го роду
Вектор-функція трьох змінних |
|
|
|
|
a |
(M) |
|
|||
|
|
a |
|
|||||||
|
P(x, y, z) |
|
Q(x, y, z) |
|
|
|
|
|||
|
i |
j |
R(x, y, z)k |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
Орієнтовані криві. Криву, для якої вибрано початкову та кінцеву точки
івказано напрям руху, називають орієнтованою.
Криволінійний інтеграл 2-го роду |
z |
|
L B |
|||||||||||||||||||||||||
від вектор-функції |
|
|
|
|
|
|
(M ) |
|
|
|
|
|
|
|
|
|
|
|||||||||||
a |
a |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
уздовж кривої L |
|
|
|
ai |
ri |
Li |
||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
O |
Mi |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
lim |
(a(Mi ), ri ) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y |
|||||||||||||||||
max |
ri |
0 |
x |
|
|
|
|
|||||||||||||||||||||
i 1 |
|
|
|
|
||||||||||||||||||||||||
n |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|||||
(a, dr ) Pdx Qdy Rdz |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
L |
L |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Фізичний зміст криволінійного |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
(F,dr ) AL(F) |
||||||||||||||||||||||||||||
інтеграла 2-го роду. Робота, яку |
||||||||||||||||||||||||||||
L |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
виконує змінна сила F F(x, y, z) під |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
час переміщення уздовж кривої L |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Основні властивості криволінійного інтеграла 2-го роду
1)(a,dr ) (a,dr ) (орієнтованість); 2) лінійність; 3) адитивність.
AB |
BA |
Обчислення криволінійного інтеграла 2-го роду
|
|
|
|
x x(t), |
|
|
|
|
|
|
|
|
|
|
|
|
|
t t |
|
L : y y(t), t |
|
||
|
1 |
|
2 |
|
|
|
|
z z(t), |
|
|
|
|
|
|
|
Pdx Qdy Rdz
L
t2
[P(t)x (t) Q(t)y (t) R(t)z (t)]dt,
t1 |
|
|
|
|
P(t) P(x(t),y(t), z(t)), |
|
|
|
Q(t) Q(x(t),y(t), z(t)), |
|
|
|
R(t) R(x(t),y(t), z(t)) |
