Файловый архив студентов. Файловый архив студентов.
1302 вуза, 5107 предмета.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Национальный технический университет Украины «Киевский политехнический институт»
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Практикум2013

.pdf
Скачиваний:
12
Добавлен:
12.05.2015
Размер:
5.25 Mб
Скачать
☆

17. Теорія поля

151

17. Теорія поля

Навчальні задачі

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

17.1.

Обчислити div

 

, якщо

 

x2

 

 

 

 

y2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

 

 

j

 

z2k

.

 

 

 

 

a

a

 

 

 

 

 

 

 

Розв’язання. [2.20.3.]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Дивергенцію знаходять за формулою

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

[2.20.3]

P

 

 

Q

 

 

 

 

R

 

 

 

 

 

 

 

 

 

 

diva

 

 

x

 

 

y

 

 

 

z

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

P(x,y,z) x2,Q(x,y,z) y2,R(x,y,z) z2;

 

[2.20.3]

 

(x2)

 

(y2)

 

 

 

(z2) 2x 2y 2z.

 

 

 

 

 

 

 

diva

 

 

y

 

z

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

17.2.

Знайти потік векторного поля

 

 

 

 

 

 

 

 

 

 

через зовнішній бік

 

 

 

 

2xi

 

2yj

zk

 

a

 

 

 

 

 

 

 

 

 

замкненої поверхні : z

x2

y2

(0

 

z H ).

Розв’язання. [2.20.8, 2.20.10.]

Потік знаходять за формулою

[2.20.8]

(a

)

 

 

 

,

 

0)d .

(a

n

 

 

 

 

Поверхня замкнена, де — поверхня конуса та — частина площини z H, що вирізається конусом. Виконано умови теореми Остроградського — Ґауса [2.20.10].

 

 

 

 

 

 

0)d

[2.20.10]

 

 

(a

)

 

 

 

,

 

 

 

divadxdydz

 

(a

n

 

 

 

 

 

 

 

 

 

 

G

 

z

 

 

 

 

 

 

 

 

0

 

 

n

 

 

 

 

 

 

O

 

 

y

x

Рис. до зад. 17.2

 

div

 

 

 

 

2x

 

 

 

(2y)

 

( z) 3

3dxdydz

a

 

x

y

z

 

 

 

 

 

 

 

 

 

 

V

 

3 dxdydz

[2.9.3]

 

 

1

 

 

 

 

 

 

 

 

 

3Vкон.

3

H 2 H H 3.

 

 

 

 

V

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Коментар. Об’єм конуса обчислюють за формулою

1

Vкон. 3 Sосн.h.

152

Розділ 2. Інтегральне числення функцій кількох змінних

17.3. Знайти потік векторного поля a 2xi 2yj zk через внутрішній бік

частини поверхні : z

x2 y2

(0 z H).

Розв’язання. [2.20.8, 2.20.10.]

 

 

Потік знаходять за формулою

[2.20.8]

(a ) (a,n 0)d .

Замкнімо поверхню поверхнею : z H. Тоді

; ..

[Деталі див. у зад. 17.2.]

z

n0

O y

x

Рис. до зад. 17.3

 

 

 

 

 

 

 

 

0)d

[2.20.10]

 

 

(

 

)

 

 

,

 

 

 

divadxdydz

a

(a

n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

G

 

diva 3 3 dxdydz H 3.

 

 

 

 

 

 

 

 

 

 

 

 

G

 

 

 

(a )

 

 

 

 

(a,n0 )d

n k ,

 

 

zd

 

 

 

 

[2.20.8]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(a,n0 ) z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

H dxdy HSкр. H 3.

 

 

 

 

 

 

 

 

 

 

DOxy

 

 

 

 

 

 

 

 

 

 

H 3 H 3 2 H 3.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Коментар. Задача відрізняється від задачі 17.2 тим, що дана поверхня незамкнена, на що вказує слово «частина» та нестрога нерівність в умові задачі. Один із способів обчислення потоку в цьому разі, полягає в замиканні поверхні й обчисленні потоку через замкнену поверхню за допомогою формули Остроградського — Ґауса.

Знак « » у формулі Остроградського — Ґауса вказує на внутрішній бік замкненої поверхні.

Частина поверхні проектується у круг D

 

: x 2

y2

H 2.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Oxy

 

 

 

 

 

 

 

 

 

 

 

 

17.4.1. Знайти ротор векторного поля

 

 

, якщо

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

xi

 

yj

zk .

a

a

r

Розв’язання. [2.20.6.]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ротор знаходять за формулою

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

 

 

j

 

 

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

[2.20.6]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Pi Qj Rk .

 

 

 

rota

 

 

 

 

 

 

 

 

 

 

 

 

 

,a

 

 

 

x

 

y

z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

P

 

Q

R

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

17. Теорія поля

153

i (z)y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

 

 

 

j

 

 

 

 

 

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

rot

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

y

 

z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

y

 

 

 

z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(y)

 

j

 

 

 

 

(z)

 

 

 

 

 

(x)

k

 

 

 

(y)

 

(x

z

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

z

 

 

 

 

 

 

 

 

 

 

 

x

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(0 0)

 

 

 

 

(0 0)

 

 

 

 

 

i

j

(0 0) k

0.

 

 

)

Коментар. Визначник розкладають за 1-м рядком. Добуток оператора частинного диференціювання на функцію означає знаходження відповідної похідної.

17.4.2. Знайти ротор векторного поля

 

 

xyi

 

 

(2x 3y z)

 

 

 

 

 

 

 

 

 

 

 

 

j

 

(z2 x2 )k

і

a

найбільшу густину циркуляції цього поля у точці M0(1; 2; 1).

Розв’язання. [2.20.6.]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

 

 

 

 

 

 

 

 

j

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

[2.20.6]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

rot

a

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

y

 

 

 

 

 

 

 

z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

xy 2x 3y z

 

x2 z2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(0 1)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

j

(2x 0) k

(2 x)

i

2xj

 

(2 x)k .

Найбільша густина циркуляції — це довжина ротора.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

max j(M0)

 

rot

 

(M0)

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

rot

 

(M0 )

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

2xj

 

(2 x)k

 

M0 (1;2; 1)

i

2j

k ;

a

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

max j(M)

 

 

 

 

 

2

 

 

 

 

 

 

 

12

( 2)2

 

 

12

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

j

k

 

 

 

 

6.

 

 

 

 

 

 

17.5. Знайти циркуляцію векторного поля

 

 

x2y3

 

 

 

 

 

 

 

 

вздовж контуру

 

 

 

 

 

i

 

 

j

 

zk

a

 

 

 

L : {x2 y2 R2, z z0} (орієнтованого проти годинникової стрілки,

якщо дивитися з додатного напряму осі Oz) за Стоксовою теоремою.

Розв’язання. [2.20.9, 2.20.11.]

Циркуляцію векторного поля знаходять за формулою

CL(a) (a,dr ).

L

Виконано всі умови теореми Стокса. За формулою Стокса

(

 

 

[2.20.11]

 

 

 

 

 

 

, 0 )dl

 

 

 

,

 

0 )d .

a

(rota

n

L

 

 

z

z0

 

 

 

k

L

 

 

 

O

 

 

y

x

Рис. до зад. 17.5

За поверхню,

напнуту на контур, вибираємо частину площини z z0, обмеже-

ної контуром

L. За одиничний вектор нормалі — вектор

 

 

 

 

 

0 k

(оскільки це

n

154

Розділ 2. Інтегральне числення функцій кількох змінних

забезпечує потрібний обхід контуру. Поверхня проектується у круг

D : x2

y2

R2.

Oxy

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

 

 

 

j

 

 

 

 

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

[2.20.6]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

0 j

0

k

( 3x2y2 ) 3x2y2k .

rota

 

 

 

 

 

 

 

 

 

 

 

 

x

y

 

z

 

 

 

x2y3

1

 

 

 

 

z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

2 2

 

 

 

2 2

 

 

 

 

 

 

 

 

(rota,n

 

) (0;0; 3x y

)

0

 

3x y

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

z z0,

 

 

 

 

 

 

 

 

 

 

 

 

 

d 1 (z )2

 

(z )2dxdy

 

 

 

 

 

dxdy.

 

 

 

 

z

z 0

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

[2.16.4]

 

 

 

 

 

 

 

 

 

 

 

 

 

[2.7.4]

 

 

 

 

 

 

C 3 x2y2d

 

3 x2y2dxdy

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

DOxy

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3 5 cos2

 

sin2

d d

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

DOxy

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

[2.3.8]

 

2

 

 

 

 

 

 

 

 

 

 

 

R

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

2

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

5

 

 

 

 

 

 

 

 

 

R

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

4

 

 

3

 

sin

d

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

d

 

cos

 

 

 

cos

 

 

d

 

 

 

 

 

 

 

cos

 

 

d

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

1

3

 

 

 

R

6

 

 

 

 

 

 

 

 

 

 

 

 

 

2R

6

 

 

 

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

2

 

 

2

 

 

 

 

 

 

8

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

17.6.1. Перевірити потенціальність поля

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

z

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a

 

 

 

 

 

 

 

2

 

i

 

 

 

 

 

 

 

 

2

j

 

 

 

 

 

 

 

2

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

z

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

і знайти його потенціал.

Розв’язання. [2.21.1, 2.21.2.]

[Перевіряємо умову потенціальності поля rota 0.]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

 

 

 

 

 

 

 

j

 

 

 

 

 

[2.20.6]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

rot

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

y

1

 

 

z

 

 

 

 

 

 

 

 

 

 

 

z

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x2

 

 

 

 

y2

 

 

 

 

 

1

 

 

 

 

1

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

2

 

 

 

 

 

2

 

 

j

 

 

 

2

 

 

 

 

 

 

y

 

 

 

 

y

 

 

 

 

 

 

 

 

 

z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

z

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

x

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

z2

 

 

 

 

 

 

1

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

k

 

2

 

 

z

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

1

0.

x2

17. Теорія поля

155

Поле a потенціальне.

[Записуємо формулу для потенціалу векторного поля a і знаходимо його.]

[2.21.2]

x

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

z

 

 

 

 

 

U(x,y,z) P(t,y0,z0 )dt Q(x,t,z0 )dt R(x,y,t)dt C.

 

x0

 

 

 

 

 

 

 

 

 

 

 

y0

 

 

 

 

 

 

 

 

 

 

 

 

 

z0

 

 

 

 

 

Вибираємо за початкову точку M0(1;1;1).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

1

 

 

 

y

 

 

 

 

1

 

 

 

 

 

z

 

 

1

 

 

x

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

U(x,y,z)

1

 

2

 

dt

 

 

 

 

 

2

dt

 

 

 

 

2

dt C

 

 

 

 

t

 

 

 

 

 

 

 

 

 

t

 

 

 

 

 

 

 

 

 

 

 

t

 

 

1

 

 

 

 

 

 

 

 

 

1

x

 

 

 

 

 

 

 

1

 

y

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

y

 

 

 

 

 

 

 

 

z

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

t

 

 

1

 

 

 

 

 

t

 

 

x

 

 

 

 

 

 

 

 

t

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

C

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

t

 

1

x

 

t

 

1

 

 

y

 

 

t

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x 1

1

1 y

1 1

 

1

z

 

1

 

x

x C

 

x

 

 

 

 

 

 

 

x

x

y

 

 

 

 

 

 

 

y

 

 

y

 

 

z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

z

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

y z

 

C.

 

 

 

 

 

 

 

 

 

 

За означенням a gradU.

17.6.2. Чи є поле a 2xyi y2zj (z2y 2yz)k соленоїдальним?

Розв’язання. [2.21.3.]

[Перевіряємо умову соленоїдальності поля div a 0.]

[2.20.3]

 

 

 

 

 

 

 

div

 

 

 

(2xy)

 

 

 

( y2z)

 

 

 

(z2y 2yz)

a

x

y

z

 

 

 

 

 

2y 2yz 2zy 2y 0.

Поле

 

— соленоїдальне.

 

 

 

 

 

 

 

 

 

 

 

 

a

 

 

 

 

 

 

 

 

 

 

 

 

17.6.3. Показати, що векторне поле

 

(y z)

 

(x z)

 

 

 

гармо-

 

i

j

(x y)k

a

нічне.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Розв’язання. [2.21.4.]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

[Перевіряємо умову гармонічності векторного поля rot

 

 

 

 

 

 

 

 

0.]

 

 

0, div

 

a

a

 

 

 

 

 

 

 

 

 

[2.20.3]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

diva

 

 

 

 

 

 

 

 

(y z)

 

(x z)

 

(x y) 0.

 

 

 

 

 

x

y

z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

 

 

 

 

j

 

 

 

 

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

[2.20.6]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(1 1)i (1 1)j (1 1)k

 

0.

rota

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

y

 

z

 

 

 

 

 

 

y z

x z

x y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Векторне поле

 

 

гармонічне.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

156

Розділ 2. Інтегральне числення функцій кількох змінних

Задачі для аудиторної і домашньої роботи

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

17.7. Нехай

 

 

 

 

 

 

 

 

 

 

 

 

x2 y2

z2 . Знайдіть grad u,

 

xi

yj zk , r

 

 

 

 

r

r

якщо:

 

 

 

 

 

 

 

 

 

 

 

 

 

1) u r2;

 

 

 

 

 

 

 

 

2) u

1 .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

r

 

 

17.8. Знайдіть дивергенцію векторного поля:

1)

 

xyzi

 

(2x 3y z)

 

(x2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

j

z2 )k

;

 

 

 

 

 

 

 

 

a

2)

 

(x y z)

 

(x2 y2 z2 )

 

 

 

 

 

 

 

 

 

 

 

 

 

i

j

(x3 y3 z3 )k

;

a

 

 

 

 

 

 

 

 

 

 

, де

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3)

 

r

4)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

xi

yj zk ;

 

 

 

 

 

 

;

a

 

 

 

 

 

 

r

a

r

r

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

r

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5) div grad(x2 y2 z2 );

6) div grad(x3 y3 z3 ).

17.9. Знайдіть ротор векторного поля:

1) a yz i xz j xy k в точці M0(1;2; 2);

2) a y2i x2j z2k ; 3) a x2yi y2zj z2xk ;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

q

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4)

 

 

 

 

 

 

 

 

xi

yj

zk .

 

 

 

 

 

rot

 

 

 

 

r , де r

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

r

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

17.10. Перевірте потенціальність і знайдіть потенціал поля:

1) a (y z)i (z x)j (x y)k ;

 

 

yzi

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2) a

 

 

zxj

xyk

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 x2y2z2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3)

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

1

 

 

 

1

 

 

 

 

yi

xj

ezk ;

4)

 

 

 

i

 

j

k

.

a

a

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

y

z

 

 

 

 

 

 

 

 

 

 

 

 

17. Теорія поля

 

 

157

17.11. З’ясуйте, чи є поле

 

(M ) соленоїдальним, якщо:

 

 

 

 

 

a

 

 

 

 

 

1)

 

x(z2 y2 )

 

y(x2 z2 )

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

j

z(y2 x2 )k

;

 

 

 

 

 

a

 

 

 

 

 

2)

 

(1 2xy)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

y2zj

(z2y 2yz 1)k ;

 

 

 

 

 

a

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3)

 

x2yzi

 

 

 

 

 

 

 

 

 

 

 

 

 

4)

 

yi

xj

xyk

 

;

 

 

xy2zj

xyz2k

;

 

 

 

 

a

 

 

a

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x2 y2

 

 

 

5) a ln(x2 y2)i 2 arctg yx j 3k .

17.12. З’ясуйте, чи є поле a(M ) гармонічним, якщо: 1) a 6x2i 3 cos(3x 2z)j cos(3y 2z)k ;

2) a (yz 2x)i (xz 2y)j xyk ;

3)a (3x2 3y2 )i (2 6xy)j ;

4)a (2x cos y 2y)i (x2 2 sin y)j .

17.13. Знайдіть потік поля a через поверхню , якщо:

1) a (x2;y2;z2 ), — зовнішній бік повної поверхні піраміди, обмеженої площинами x y z 1, x 0, y 0,z 0;

2)a y2zi yz2 j x(y2 z2 )k , — повна зовнішня поверхня цилі-

ндра y2 z2 a2, 0 x a;

3)a (0;y2;z), — обмежена частина внутрішнього боку параболоїда z x2 y2, відтятої площиною z 2;

4)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2xi

yj zk , — частина внутрішнього боку параболоїда

a

y2 z2 Rx, яку відтинає площина x R;

 

 

5)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

—

повна зовнішня

поверхня

конуса

 

 

 

 

 

 

2xi

2yj

zk ,

 

a

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x2 y2 z H;

 

 

 

 

6)

 

 

 

x2yi

xy2

 

xyzk

 

,

 

— зовнішній бік

повної

поверхні

 

 

 

 

 

j

 

 

a

x2 y2 z2 R2,x 0,y 0,z 0;

158

Розділ 2. Інтегральне числення функцій кількох змінних

7)

 

 

 

 

 

(x;y;z),

 

—

зовнішній бік

повної

поверхні

a

r

z 4 x2, 2x y 4, x 0, y 0, z 0;

 

 

 

8)

 

(x z3y;xz;z xy),

 

— зовнішній бік

повної

поверхні

a

x 0, x 1, y 0, y 2, z 0, z

x2

 

y2

.

 

 

4

6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

17.14.Обчисліть за Стоксовою теоремою циркуляцію векторного поля a вздовж контуру L, орієнтованого за годинниковою стрілкою, якщо ди-

витись із початку координат, якщо:

1) a z2i x2j y2k,L : {x2 y2 z2 1,x y z 1};

2) a (y z)i (z x)j (x y)k ,

L : {4(x2 y2) z2,x y z 1};

3) a x3i y3j z3k,L : {z x2 y2,z y 2};

4) a yi xj zk,L : {x2 y2 z2 4,x2 y2 z2,z 0}; 5) a z2j x2k,L : {y2 z2 9, 3z 4x 5};

6) a zxi xyj yzk,L : {y2 z2 1,x y z 1}.

Відповіді

17.7.1) grad r2 2r ; 2) grad r1 rr3 .

17.8.1) yz 3 2z; 2) 1 2y 3z2; 3) r2 ; 4) 4 r ; 5) 6; 6) 6x 6y 6z.

17.9.1) 54 i j 52 k ; 2) 2(x y)k ; 3) y2i z2j x2k ; 4) 0.

17.10.1) xy yz zx C; 2) arctg(xyz) C; 3) xy ez C ; 4) ln(xyz) C.

17.11.1) ні; 2) так; 3) ні; 4) так; 5) так.

17.12.1) ні; 2) так; 3) так; 4) ні.

17.13. 1)

1

;

2)

 

a5

; 3) 2 ; 4)

R3;

5) H 3; 6)

R5

; 7) 40;

8) 14.

4

4

3

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

 

 

 

 

17.14. 1)

3

; 2) 0; 3) 0; 4) 4 ; 5) 0;

6) .

 

 

 

 

 

9

 

 

 

 

 

 

 

 

 

Розділ 3. ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ

18. Диференціальні рівняння з відокремлюваними змінним

Навчальні задачі

18.1. Зінтегрувати диференціальне рівняння xy y y3.

Розв’язання. [3.2.2.]

Це диференціальне рівняння з відокремлюваними змінними.

[Підставляємо в диференціальне рівняння y dydx .]

x dydx y3 y.

[Відокремлюємо змінні, множачи обидві частини рівняння на dx і ділячи на x(y3 y).]

 

 

 

 

xdy (y3 y)dx;

 

dy

dx ,y 0.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y3 y

 

 

x

 

 

 

 

 

 

 

[Інтегруючи, дістаємо загальний інтеграл ДР.]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dy

 

dx

;

 

dy

 

 

 

ydy

 

 

dx

.

 

 

 

 

 

 

 

 

 

 

x

y

 

 

 

 

 

 

 

 

x

 

y(y

2

1)

y

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

ln

 

y

 

 

1

ln(y2 1)

ln

 

x

 

ln

 

C

 

 

(C 0);

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Cx (C

0).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y2 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Для C 0

одержимо функцію y 0,

яка є розв’язком рівняння (його можна

було б втратити під час відокремлення змінних). Загальний інтеграл рівняння

yC,C .

xy2 1

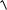
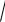18.2.Розв’язати задачу Коші: 1 y2dx 1 x2dy 0,y(0) 1.

Розв’язання. [3.1.2, 3.2.2.]

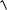
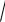Це задача Коші для диференціального рівняння з відокремлюваними змінними 1 y2dx 1 x2dy 0 і початковою умовою y(0) 1.

160

Розділ 3. Диференціальні рівняння

 

 

dy

 

 

 

 

dx

 

,x 1,y 1.

 

 

 

 

 

 

 

 

 

 

 

 

1 y2

1 x2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dy

 

 

 

 

dx

 

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 y2

 

 

 

 

1 x2

 

 

arcsin y C

 

arcsin x; arcsin x arcsin y C.

Функції x 1,y 1 є розв’язками ДР, але ці розв’язки не можна отримати за жодного значення сталої C — це особливі розв’язки.

Частинний інтеграл знайдемо з початкової умови y(0) 1 :

arcsin 0 arcsin 1 C C

.

 

 

Розв’язок задачі Коші задає співвідношення

 

 

2

 

 

 

 

 

 

 

arcsin x arcsin y ; arcsin y

 

 

 

 

arcsin x y

1 x2 .

2

2

 

 

 

 

Коментар.arcsin y arccos x; y sin(arccos x) 1 x2 .

18.3.Матеріальна точка маси m рухається прямолінійно під дією сили F, прямо пропорційної часу від початку руху і обернено пропорційної швидкості руху v. Встановити залежність між швидкістю і часом, якщо

v |t 0 0.

Розв’язання. [3.1.2, 3.2.2.]

[Скористаємось фізичним змістом задачі.]

Згідно із другим законом Ньютона

F ma m dv .

Для знаходження v(t) маємо задачу Коші:

 

 

 

dt

 

 

 

 

 

 

m dv

kt

;v(0) 0.

 

dt

 

v

 

 

 

 

 

 

 

 

 

[Розв’яжімо її.]

 

 

 

 

 

 

 

 

 

 

 

 

 

k

 

 

 

 

 

 

 

 

 

 

k

vdv

 

tdt; vdv

 

tdt;

m

m

v2

 

k

 

 

t2

 

C;

2

 

m

2

 

 

 

 

 

 

 

 

 

 

v(0) 0 C 0.

 

 

 

 

 

 

 

Розв’язком задачі Коші є функція v(t)

 

 

 

k

t.

 

 

 

 

 

 

 

 

 

 

 

 

 

m
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности