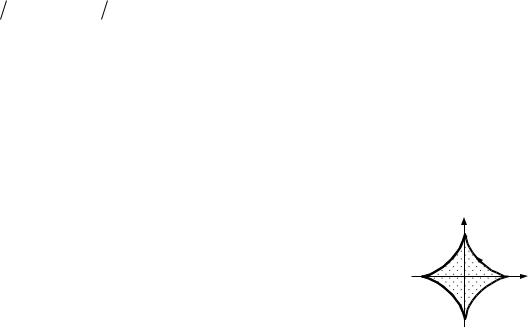Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный технический университет Украины «Киевский политехнический институт»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Практикум2013

.pdf

Скачиваний:

Добавлен:

12.05.2015

Размер:

5.25 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 2014 15 16 17 18 19 20 > Следующая >>>

13. Обчислення криволінійного інтеграла 2-го роду

131

13. Обчислення криволінійного інтеграла 2-го роду

Навчальні задачі

13.1.1. Обчислити xydx zdy (x2 y2 )dz,

Розв’язання. [2.13.6.]

Інтеграл обчислюємо за формулою [2.13.6]:


x a cost,


	0	t
де L: y a sint,	0	t	.

			2
			2
z bt,

					t2

	Pdx Qdy Rdz [P(t)x (t) Q(t)y (t) R(t)z (t)]dt,
	L				t1

де P(t) P(x(t),y(t),z(t)),Q(t) Q(x(t),y(t),z(t)),R(t) R(x(t),y(t),z(t))
	P(x, y, z) xy,Q(x, y, z) z, R(x, y, z) x2 y2;
			2					2	.
		P(t) a		sin t cos t,Q(t) bt, R(t) a					.
		x a sin t, y a cos tdt, z bdt.
					[2.13.6] 2
xydx zdy (x2 y2 )dz						a3 cost sin2 t bat cost a2b dt
L						0
		2				2	2
	ab t costdt a2b dt a3 cost sin2 tdt
	0					0	0			[2.3.3]
		u t				du dt				[2.3.3]
		u t				du dt	;cos tdt d(sin t)
		dv costdt				v sin t	;cos tdt d(sin t)

		2	a	3		3		2		a	3
				3				2			3

					sin							ab		ab
	ab cost abt sin t a bt				sin		t					ab		ab
			3							3			2
			3					0		3			2
								0
Коментар.  Крива L є циліндричною гвинтовою лінією.
13.1.2. Обчислити		(x3 y)dx (x y3 )dy,							уздовж ламаної

a2b . 2

ABC, якщо

ABC

A(1;1), B(3;1),C(3;5).

Розв’язання. [2.13.8.]

Оскільки ламана складається з ланок AB та BC, то

	[2.13.5]		.

ABC		AB	BC

Інтеграли обчислюємо за формулою [2.13.8].

132	Розділ 2. Інтегральне числення функцій кількох змінних

						[2.13.8] b
	P(x,y)dx Q(x,y)dy [P(x,y(x)) Q(x,y(x))y
	P(x,y)dx Q(x,y)dy [P(x,y(x)) Q(x,y(x))y																(x)]dx.
	L						a
На відрізку AB : y 1,y 0,x [1;3].
		3			3	3		3						4		3
						3								4		3
												x

	(x		y)dx (x y			)dy (x			1)dx								22.
	(x		y)dx (x y			)dy (x			1)dx				4		x		22.
AB						1							4			1
AB						1										1
На відрізку BC : x 3, x 0, y [1; 5].
				3		3				5		3						y	4	5
										5									4	5


				(x y)dx (x y )dy							(3 y )dy 3y
				(x y)dx (x y )dy							(3 y )dy 3y							4
			BC							1								4		1
					(x3	y)dx (x y3)dy 22 168											190.
					ABC

5 C

1 A B O 1 3 x

Рис. до зад. 13.1.1

168.

13.2.1. Обчислити інтеграл		(1 x2 )ydx x(1 y2 )dy за формулою
	L:x2 y2 R2

Остроградського — Ґріна і безпосередньо.

Розв’язання. [2.13.7, 2.13.9.]

[Записуємо формулу Остроградського — Ґріна і перевіряємо умови її застосовності.]

			Q
			Q	P
	Pdx Qdy
	Pdx Qdy			dxdy
L		D	x	y

де

P(x,y) (1 x2 )y,Q(x,y) x(1 y2 ).

Оскільки ці функції неперервні і мають неперервні частинні похідні в замкненій області D, коло є гладкою кривою, то формула Остроградського — Ґріна застосовна.

R x

Рис. до зад. 13.2.1

		[2.13.9]		Q	1 y2,
(1 x2 )ydx x(1 y2 )dy				x
(1 x2 )ydx x(1 y2 )dy				P	1 x2
L				y
(1 y2	(1 x2 ))dxdy (x2				y2 )dxdy		[2.7.4]
(1 y2	(1 x2 ))dxdy (x2				y2 )dxdy
D		D
		R
3d d d 3d 2 R4						R4 .
		0			4	2
D		0
[Обчислюємо криволінійний інтеграл безпосередньо.]

		x R cos t,
Параметризуємо рівняння кола: L :			(0 t 2 ).
Параметризуємо рівняння кола: L :			(0 t 2 ).
		y R sin t,

13. Обчислення криволінійного інтеграла 2-го роду				133
			[2.13.7]
(1 x2)ydx x(1 y2)dy
L
2
((1 R2 cos2 t)R sint( R sint) R cost(1 R2 sin2 t)R cost)dt
0
2
(R2 cos 2t 2R4 sin2 t cos2 tdt) R4.
0			2
0
13.2.2. Обчислити інтеграл			xdy ydx безпосередньо і за формулою
		R2	x2 y2
	L:x2 y2	R2

Остроградського — Ґріна.

Розв’язання. [2.13.7, 2.13.9.]

[Обчислюємо інтеграл безпосередньо, параметризуючи криву.]

x R cost,

L :

(0 t 2 ).

y R sint,

xdy ydx

[2.13.7 ] 2

cos2 t R2 sin2 t

cos

sin

dt 2 .

[Перевіряємо умови застосовності формули Остроградського — Ґріна.]

Функції P(x, y)

,Q(x, y)

мають розрив в точці O(0; 0),

яка лежить усередині круга x2 y2

R2.

Формула Остроградського — Ґріна не застосовна.

Коментар.  Ось чому, хоча і

, (x;y)

D \ O,

y x

криволінійний інтеграл може бути відмінним від нуля.

13.3.1. Перевірити чи є підінтегральний вираз повним диференціалом та обчис-

(1;1)

лити (x2 y2 )dx 2xydy.

(0;0)

Розв’язання. [2.15.2.]

[Перевіряємо умову того, що підінтегральний вираз є повним диференціалом і криволінійний інтеграл не залежить від шляху інтегрування.]

	P(x, y) x2 y2,Q(x, y) 2xy.
P	Q	:		(x2 y2) 2y		( 2xy).
y	x		y		x

134	Розділ 2. Інтегральне числення функцій кількох змінних

Оскільки підінтегральний вираз є повним диференціалом, то інтеграл не залежить від того, якою лінією сполучено точки O(0; 0) і A(1;1).

Обчислюємо інтеграл вздовж прямої y x, x [0;1].

(1;1)					[2.13.8]
(x2 y2)dx 2xydy				(x2 y2)dx 2xydy
(0;0)			y x,
			x [0;1]
1				1	2.
	y 1	(0 2x2 1)dx 2 x2dx
	y 1	(0 2x2 1)dx 2 x2dx
					3
0				0	3
0				0

13.3.2. Перевірити чи є підінтегральний вираз повним диференціалом та обчис-

(3;2;1)
лити	yzdx zxdy xydz.
(1;2;3)

Розв’язання. [2.15.1.]

[Перевіряємо умови того, що підінтегральна функція є повним диференціалом і криволінійний інтеграл не залежить від шляху інтегрування.]

	P yz,Q zx,R xy.
Q		P	:	(zx)	z	(yz)			;
x		y		x			y

R		Q	:	(xy)	x		(zx)		;
y		z		y			z

P		R	:	(yz)	y	(xy)		.
z		x		z
							x

Вибираємо за шлях інтегрування ламану ACB, де A(1;2;3), C(3;2;3),B(3;2;1):

(3;2;1)

yzdx zxdy xydz

(1;2;3)

ACB

AC CB

yzdx zxdy xydz

AC :x t,

CB:x 3,

y 2,z 3,

y 2,z t,

t [1;3]

t [3;1]

2 3dt 3 2dt 0.

Коментар.  Ця умова еквівалентна тому,

що rot F

0, де

Rk .

13. Обчислення криволінійного інтеграла 2-го роду

135

Задачі для аудиторної і домашньої роботи

13.4. Обчисліть криволінійний інтеграл:

1)	xdy ydx, де L — дуга кривої y x3							від точки A(0; 0) до точки
	L
B(2; 8);
2)			y	dx dy, де L			— дуга кривої y ln x	від точки A(1; 0) до точки
2)				dx dy, де L			— дуга кривої y ln x	від точки A(1; 0) до точки
	L		x
	L
B(e;1);

		2			2			x a cost,
3)		2			2	де			що об-
3)		y dx x dy,				де	L — верхня половина еліпса		що об-
								y b sint,
	L
	L

ходиться проти руху годинникової стрілки;

4)		(x y)dx (x y)dy							, де L — коло x2 y2 a2;

			x	2	y		2
	L		x		y
	L
5)	xdx ydy (x y 1)dz, де L — відрізок AB від точки
	L
A (1;1;1) до точки B(2;3; 4);
6)	ydx zdy xdz,							де L — перший виток конічної гвинтової лінії
	L							bt, у напрямі збільшення параметра.
x a cost,y a sin t,z								bt, у напрямі збільшення параметра.
13.5. Обчисліть криволінійний інтеграл:
1)	xdy ydx,					де L : а) відрізок AB від точки A(0;0) до точки B(1;2);
	L
б) дуга параболи y 2x2, від точки A до точки B; в) ламана ACB, де
C(1;0);
2)	2xydx x2dy, де L : а) відрізок прямої y x від точки A(0; 0) до
	L

точки B(1;1); б) дуга параболи y x2 від точки A до точки B.

13.6. Застосовуючи формулу Остроградського — Ґріна, обчисліть криволіній-

ний інтеграл уздовж кривої L :

136	Розділ 2. Інтегральне числення функцій кількох змінних

1)	(2xy y)dx x2dy, де L — еліпс x		2	y	2	1;
1)	(2xy y)dx x2dy, де L — еліпс x		2	y	2	1;
	L	a		b
	L
2)	(x y)2dx (x2 y2)dy, де L			—	трикутник			з		вершинами
	L
O(0;0),A(1;0), B(0;1);
3)	(1 x2)ydx x(1 y2)dy, де L — коло x2					y2 R2;
	L
							2	2
4)	(xy x y)dx (xy x y)dy, де L : а) еліпс x								y	1; б) ко-
4)	(xy x y)dx (xy x y)dy, де L : а) еліпс x						2		2	1; б) ко-
	L					a			b
	L

ло x2 y2 ax.

13.7.Переконайтесь у тому, що підінтегральний вираз є повним диференціалом і обчисліть криволінійний інтеграл:

(2;3)

(1;1)

xdy ydx;

(x y)(dx dy);

( 1;2)

(0;0)

(1;1)

y dx

x dy;

(0;1)

( ;2)

sin

cos

dy.

( ;1)

Відповіді

13.4.1) 8; 2) 32 ; 3) 43 ab2; 4) 2 ; 5) 13; 6) a2.

13.5.1) а) 0; б) 23 ; в) 2; 2) а) 1; б) 1.

13.6. 1)	ab; 2) 1;	3)		R4	; 4) а) 0;	б)	a 3	.
				2			8

13.7. 1)	8; 2) 2; 3)
			2; 4) 1 .

14. Застосування криволінійного інтеграла 2-го роду

137

14. Застосування криволінійного інтеграла 2-го роду

Навчальні задачі

під час переміщення вздовж верхньої по-

14.1. Знайти роботу сили F

ловини еліпса

(y 0) від точки M(a;0) до точки N( a;0).

Розв’язання. [2.14.1.]

вздовж кривої L знаходять за

Роботу силового поля F

формулою

[2.14.1]

AL(F) P(x,y)dx Q(x,y)dy ydx xdy

a x

Рис. до зад. 14.1

Параметризуємо шлях переміщення:

		a cost,
	x	a cost,

		b sint,
	y	b sint,


	[2.13.7]
A ydx xdy		(b sint
L		0

0 t .

( a sint) a cost b cost)dt

ab (sin2 t cos2 t)dt ab.

14.2. Знайти циркуляцію векторного поля

x2y3

вздовж конту-

ру L : {x2 y2 R2, z z0 }

(орієнтованого проти годинникової стрі-

лки, якщо дивитися з додатного напряму осі Oz).

Розв’язання. [2.14.2.]

Циркуляцію векторного поля

вздовж кривої L

знаходять за

формулою

[2.14.2]

) Pdx Qdy Rdz

CL(a

x2y3dx dy zdz.

Рис. до зад. 14.2

Параметризуємо рівняння кола L.

R cost,

R sin t,

0 t

2 .



138	Розділ 2. Інтегральне числення функцій кількох змінних

							) x2y3dx dy zdz							[2.13.6]

				CL(a
			2					L
			2
			(R2 cos2 t R3 sin3 t( R sint) R cost 0)dt
			0
				2					2						20
				R6 sin6 tdt R6 sin4 tdt R sint


	2				0				0
	2				2													6
								[2.3.8]				1	3	5		1 3	R	6
6			6	tdt		4			4R	6		1	3	5		1 3	R	.
4R			sin	tdt		sin		tdt	4R									.

													4	6			8
		0			0						2 2		4	6	2 2 4		8
		0			0

Коментар.Змінювання параметра t від 0 до 2 відповідає напряму обходу контуру, заданого в умові задачі.

				3
			a cos t,
		x	a cos t,		0	t 2 .
14.3. Знайти площу фігури, обмежену астроїдою			a sin3 t,		0	t 2 .
		y	a sin3 t,
Розв’язання. [2.14.3.]
Розв’язання. [2.14.3.]						y
Площу фігури D, обмежену замкненим контуром L, обчис-						y
люють за формулою:						L
[2.14.3]	1	xdy ydx.				OD	x
S(D)	2	xdy ydx.
		L
S 21 xdy ydx		x 3a cos2 t sint,				Рис. до зад. 14.3
		x 3a cos2 t sint,				Рис. до зад. 14.3
		y 3a sin2 t cost
L

1 (3a2 sin2 t cos4 t 3a2 sin4 t cos2 t)dt 2 0

3a2	2	2		3a8		2			2								316a2		2
3a2	2	sin2 t cos2 tdt		3a8		2			sin2 2tdt								316a2		(1 cos 4t)dt
		0							0			2								0
			3a	2											3 a			2
				2														2
									sin 4t										.
				t															.
										4							8
			16							4		0					8
												0
14.4. Знайти функцію u за її повним диференціалом
			2x(1 e				y	)					e	y
			2x(1 e					)					e

		du								dx							1
		du								dx							1			dy.
			(1 x		2		2						x			2
			(1 x		)						1		x

Розв’язання. [2.15.2, 2.15.5.]

[Переконуємося в тому, що du є повним диференціалом.]:

14. Застосування криволінійного інтеграла 2-го роду

139

P(x,y)

2x(1 ey )

,Q(x,y)

x2)2

1 x2

[2.15.2]

2xe

2x(1 e

)

(1 x

)

(1 x

)

Вираз du є повним диференціалом. Функцію u(x, y) відновлюють за формулою

	e	y
	e
				1

					.
x	1 x		2
			2

[2.15.5]

u(x,y)

P(t,y0)dt Q(x,t)dt C.

Вибираємо за початкову точку M0(0; 0). 

u(x,y)

0dt

0 1

y C.

1 x

Коментар.  Точку M0(x0;y0 ) можна вибирати довільно, але так, щоб функ-

ції P(x, y) та Q(x, y) були у ній неперервними.

Запис P(t,y0 ) означає, що у функцію P(x, y) підставляють t замість x і y0 за-

мість y.

Запис Q(x, t) означає, що у функцію Q(x, y) підставляють t замість y, а змінну x залишають без змін і під час інтегрування вважають сталою.

Задачі для аудиторної і домашньої роботи

14.6. Знайдіть роботу поля F під час переміщення точки вздовж дуги кривої

L від точки A до точки B, якщо:

2xyi

,L : y x2 1,A(1;0),B(2;3);

3xy2

(x y)

, L : y2 x 1, A(0;1),B(3;2);

xy2

, L AB, A(0;1), B(1;2);

F x

j , L : xy

1, A(1;1), B

;

,L : x2 y2

1,y 0,A(1;0), B( 1;0);

2xj

x a cost,

F 2xj , L

A(a;0),B a;0

;

y b sint,

140	Розділ 2. Інтегральне числення функцій кількох змінних

x a(t

sin t),

F yi xj ,L :

A(0;0),B(2 a;0);

cost),

y a(1

a cos

F yi xj ,L :

A(a;0),B

;

y a sin

9) F (y2 z2 )i yzj xk ,L : x bt,y a cost,z a sin t, A(0;a;0),

;0;a ;

10)

yk , L : x t, y t cos t, z t sin t, A(0; 0; 0),

B(2 ; 2 ; 0).

14.6.

1. Знайдіть роботу поля F

(4x 5y)

(2x y)

під час переміщен-

ня вздовж кривої L від точки A(1; 9)

до точки B(3; 3), якщо:

а) L — ламана APB, де P(1; 3);

б) L — ламана AQB, де Q(3; 9).

2. Знайдіть роботу поля F

під час переміщення вздовж

кривої L від точки O(0;0) до точки B(1;1), якщо:

а) L — ламана OAB, де A(1;0);

б) L — ламана OCB, де C(0;1).

14.7.

Знайдіть модуль циркуляції векторного поля

вздовж контуру L, якщо:

, L : {x y z

3,x 0,y 0,z 0};

x2k

xk ,L : {x2

R2, x 0,y 0,z 0};

zk , L : {x2

4, x2 y2 z2, z 0};

,L : {z x2 y2

10,z 1}.

14.8.

Обчисліть площу фігури, обмежену:

1) еліпсом x2 y2 1; a2 b2

2)кардіоїдою x a(2 cost cos 2t), y a(2 sin t sin 2t).

14.9.Відновіть функцію u за її повним диференціалом:

1)du (e2y 5y3ex )dx (2xe2y 15y2ex )dy;

2)du (3x2 2xy y2 )dx (x2 2xy 3y2 )dy;

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 2014 15 16 17 18 19 20 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.2025100.53 Кб0практика.docx
#
12.05.2015165.58 Кб16практика.pdf
#
17.03.2016393.04 Кб15ПРАКТИКА_ФММ1.docx
#
17.03.20165.29 Mб53Практикум 2.pdf
#
01.05.2025305.66 Кб0Практикум зі складання МЕТОДИЧКА.doc
#
12.05.20155.25 Mб12Практикум2013.pdf
#
17.03.20162.86 Mб56Практикум_Ромашко.pdf
#
01.03.2025136.19 Кб0Практическая работа7.doc
#
01.05.20253.59 Mб0Практическая_часть-WordPress.doc
#
01.03.2025402.94 Кб2Практичні роботи 1-6.doc
#
12.05.201524.81 Кб180Практичні роботи.docx