|
10. Застосування подвійного інтеграла |
|
|
|
111 |
|
[2.7.4] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S dxdy |
|
d d |
|
|
6 |
2 ; |
|
|
|
D |
|
|
D |
|
|
|
|
|
4 sin 8 sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
8 sin |
|
2 |
2 |
|
8 sin |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
d |
2 |
|
4 sin |
d 24 sin2 d |
6 |
4 sin |
|
6 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 2 |
|
|
|
|
|
|
|
|
|
12 1 cos 2 d 12 |
|
|
|
|
|
4 3 |
3. |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
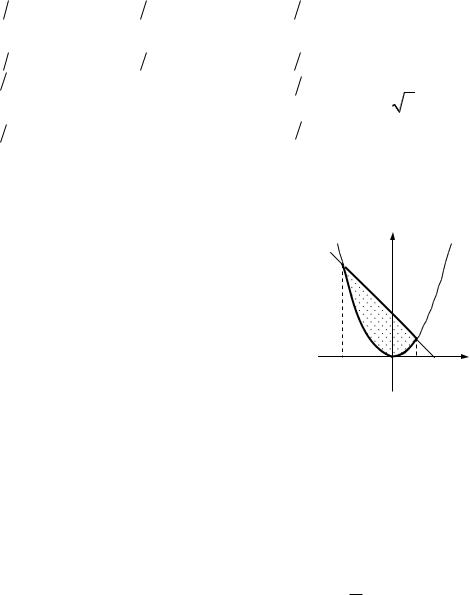
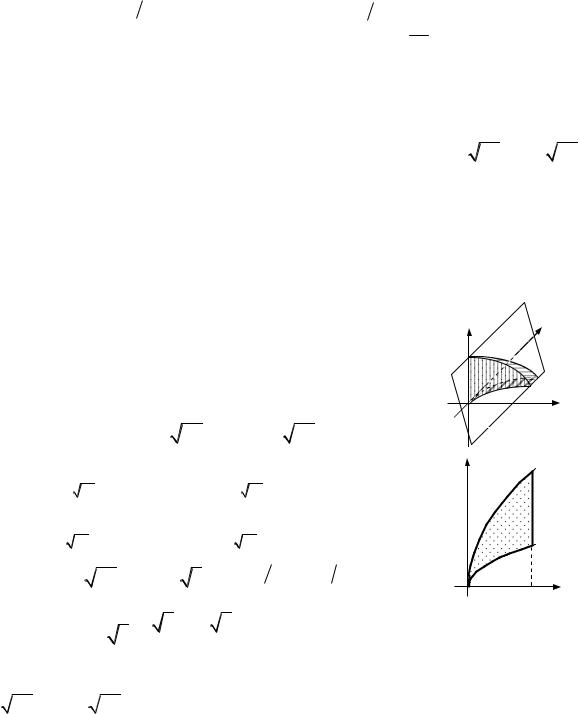
10.2.1.Знайти масу пластинки D, яка обмежена лініями 2y x2, x y 4, з густиною розподілу маси (x, y) 2.
Розв’язання. [2.8.2.]
Масу пластинки D з густиною (x, y) знаходять за формулою
[2.8.2] |
(x, y)dxdy 2dxdy. |
m(D) |
|
D |
D |
Область D правильна в напрямі осі Oy. Залишаємось у декартових координатах.
[Щоб визначити межі інтегрування знайдемо абсциси точок перетину параболи з прямою.]
|
|
2 |
, |
|
|
|
|
x |
|
|
2y x |
|
2 |
|
|
1 |
|
|
|
|
x |
2x 8 0 |
|
|
|
|
|
|
|
|
|
x |
y 4 |
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y
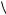
 D 4
D 4
4 2 x
Рис. до зад. 10.2.1
4,
2.
|
|
|
|
|
|
4 x 2, |
|
|
|
m 2 dxdy |
зверху y 4 x, |
|
|
D |
|
|
|
знизу y |
x2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
4 |
x |
|
|
|
4x |
|
|
|
|
|
|
dx 2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
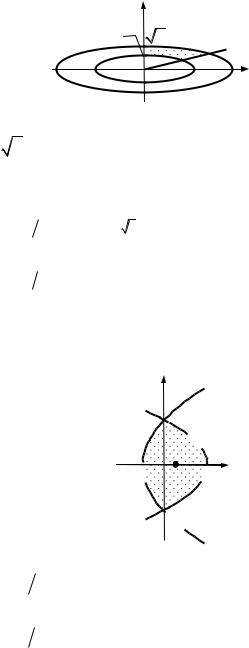
10.2.2. Знайти |
масу пластинки D, яку задано нерівностями |
y x |
0, |
|
|
|
|
|
|
|
4 |
|
1 |
x2 |
y2 3, з густиною розподілу маси (x,y) |
x |
. |
|
|
|
|
|
y5 |
|
|
16 |
|
|
|
|
|
|
|
|
|
Розв’язання. [2.8.2.]
112 |
Розділ 2. Інтегральне числення функцій кількох змінних |
Масу пластинки D з густиною (x, y) знаходять за формулою
|
|
|
|
|
[2.8.2] |
(x, y)dxdy |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m(D) |
|
|
|
|
dxdy. |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
D |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
Виходячи з форми пластинки доцільно перейти до |
|
|
|
|
|
|
|
|
|
|
|
узагальнених полярних координат [2.1.3]: |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
D |
|
|
|
|
|
4 cos , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y sin , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J |
4 . |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. до зад. 10.2.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 3; 1 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 sin 4 cos 0; tg 1; |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
x |
|
|
4 cos |
|
|
|
|
cos |
|
3 d |
|
m |
|
|
dxdy |
|
|
|
|
|
4 d d 16 |
|
|
|
|
d |
|
|
|
|
4. |
y |
5 |
|
4 |
sin |
5 |
|
|
sin |
5 |
|
|
3 |
|
D |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
1 |
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10.3. Знайти координати центра маси однорідної матеріальної пластини, обмеженої кривими y2 4x 4, y2 2x 4 .
Розв’язання. [2.8.4]
Пластина однорідна, тому (x, y) 0 const .
Пластина симетрична відносно осі Ox , тому yC 0.
Абсцису центра маси шукають за формулою
|
|
|
x |
|
|
My |
, |
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
де My |
|
1 |
0xdxdy; |
m 0dxdy. |
|
|
m |
|
|
|
D |
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
(4 y2 ) 2 |
|
|
|
|
My x 0dxdy 0 dy |
|
xdx |
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
(y2 4) 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
1 |
|
|
|
2 |
|
2 |
|
|
|
1 |
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
4 y |
|
|
|
|
|
y |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
2 |
|
|
|
|
|
2 |
|
|
|
4 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
8y |
3 |
|
y |
5 |
|
|
2 |
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 8y |
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
y |
|
|
|
|
|
0 |
|
16y |
|
|
|
|
|
|
|
|
|
|
|
|
0. |
16 |
|
|
|
|
16 |
|
3 |
|
5 |
|
|
5 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10. Застосування подвійного інтеграла |
|
|
|
|
113 |
|
|
2 |
|
|
(4 y2 ) 2 |
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m 0dxdy 0 dy |
|
|
|
dx 0 |
|
|
|
|
|
4 |
y |
|
|
|
y |
|
4 dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
D |
|
2 |
|
(y2 4) 4 |
|
2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3 2 |
|
|
|
|
|
|
|
|
|
|
y |
3 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
|
|
3 |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
8 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
2 3y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
x |
c |
|
|
16 0 |
|
1 |
|
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Центр маси даної пластини міститься в точці C |
|
|
|
|
|
; 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
Задачі для аудиторної і домашньої роботи
10.4. Обчисліть площі фігур, обмежених лініями:
1) y2 2x, y x; 2) y x2, y 2x x2;
|
|
|
|
|
|
3) |
x 0, y x, y 2 x2 (x 0); 4) x2 y2 4, y2 4 4x, x 1; |
5) x2 y2 2x, x2 y2 4x, y x, y 0; |
6) x2 y2 3y, x2 y2 5y, y |
x |
|
, x 0; |
|
|
|
|
 3
3
7) (x2 y2 )2 x2 y2, x2 y2 
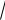 2x 0;
2x 0;
8) a(1 cos ), a cos (a 0);
|
|
2 |
|
|
y |
2 |
2 |
|
x |
2 |
|
y |
2 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
9) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(лемніската); |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
9 |
|
|
|
4 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
y |
2 |
2 |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
10) |
|
|
|
|
|
|
|
|
4xy |
(лемніската); |
|
|
|
|
|
|
|
|
9 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11)x2 3y, x2 4y, y2 x, y2 2x;
12)y2 ax, y2 bx, xy , xy (0 a b, 0 ).
10.5. Знайдіть масу пластини D з густиною (x, y):
|
1) |
D : x 2 |
y2 |
4, x2 y2 16, x 0, |
y 0, (x,y) |
y x |
|
; |
|
x2 y2 |
|
|
|
|
|
|
|
|
|
|
|
|
2) D : x2 |
y2 |
1, x2 y2 9, x 0, y 0, (x,y) |
|
x |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
D : (x2 |
y2)2 |
a2(x2 y2) (x 0), |
|
|
|
|
|
|
|
3) |
(x,y) x x2 |
y2 ; |
|
|
|
4) |
D : (x2 |
y2)2 |
9(x2 y2) (x 0,y |
0), (x,y) x2 y2; |
|
|
114 |
Розділ 2. Інтегральне числення функцій кількох змінних |
5) D : x2 y2 ax, x2 y2 2ax,y 0, (x,y) x2 y2;
|
6) D : 1 |
x2 |
|
y2 |
2, x 0, x |
4 |
y, (x,y) |
27x |
. |
|
16 |
9 |
3 |
y5 |
|
|
|
|
|
|
10.6.Для пластинки D з густиною (x, y) знайдіть: а) масу; б) координати центру мас; в) моменти інерції щодо осей Ox та Oy, якщо:
1)D : x2 y2 2ax, (x,y) 0 
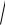 x2 y2 ;
x2 y2 ;
2)D : x y a,a x 0,a y 0, (x,y) x.
Відповіді
|
|
2 ; |
|
1 ; |
|
7 |
|
|
|
6 8 |
|
5) 3 |
|
3 |
|
|
4 |
|
|
|
|
|
10.4. 1) |
2) |
3) |
; 4) |
; |
|
; |
6) |
|
|
|
3; 7) |
6 |
|
2 |
3 |
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
10) 72; 11) |
1 |
; |
12) |
1 |
( )ln b . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10.5. 1) 4; 2) 4; 3) |
2 |
|
|
|
2 a4 ; |
4) |
|
81 |
; 1) |
45 |
a4 ; |
4) 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
32 |
|
|
64 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
3 |
|
; б) |
x |
6 |
a,y |
0; |
в) |
I |
|
|
|
512 |
a |
5 |
|
, I |
|
10.6. 1) а) |
|
a |
0 |
|
xx |
|
|
|
|
0 |
yy |
|
|
|
|
9 |
|
|
|
|
|
|
|
C |
5 |
|
C |
|
|
|
|
|
|
|
|
525 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) а) |
a3 |
; б) x |
|
3a |
, y |
5a |
; в) I |
|
|
3a5 |
, I |
|
|
a5 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
xx |
|
|
|
yy |
|
|
|
|
|
|
|
3 |
|
|
C |
|
|
4 |
|
|
|
C |
8 |
|
|
|
|
|
20 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 ; 8) 5 a2; 9) 6;
2 4
1024 5
175 a 0;
11. Потрійний інтеграл
Навчальні задачі
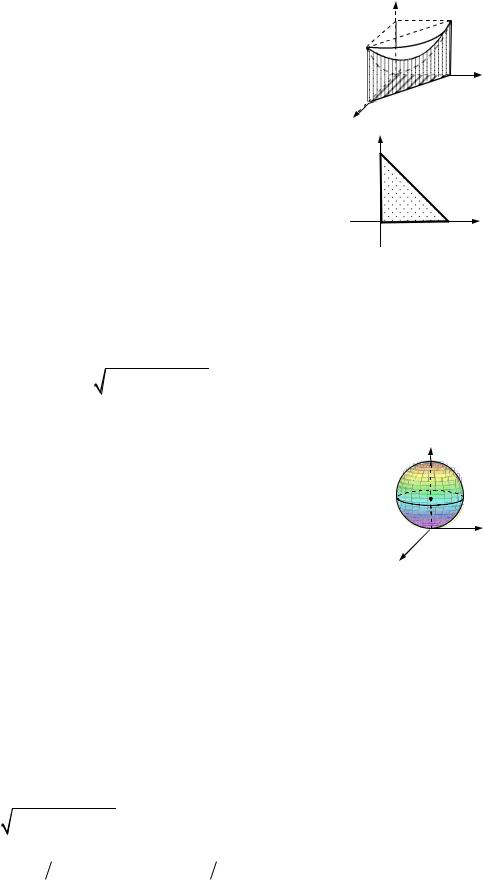
11.1. Обчислити I zdxdydz, якщо область G обмежена поверхнями:
G
z x2 y2, x y 1, x,y,z 0.
Розв’язання. [2.9.4.]
Область інтегрування G є циліндричною в напрямі осі Oz.
знизу площиною z 0, зверху — параболоїдом z x2 y2. на площину Oxy .
|
[2.9.4] |
|
зверху z x2 y2, |
|
|
x2 y2 |
|
|
|
|
zdxdydz |
|
|
dxdy |
|
|
|
знизу z 0 |
|
G |
|
|
|
|
DOxy |
0 |
|
|
|
|
z2 |
|
x2 |
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dxdy |
|
|
|
|
|
2 |
|
0 |
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
Oxy |
|
|
|
|
|
|
|
Вона обмежена:
Проектуємо тіло
zdz
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11. Потрійний інтеграл |
|
|
|
|
|
|
|
|
|
|
115 |
|
|
|
1 |
|
|
(x |
|
y |
|
|
|
|
|
|
|
0 x 1, |
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
) dxdy |
зверху y 1 x, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
DOxy |
|
|
|
|
|
|
|
|
|
|
|
|
знизу y 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
1 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx (x4 2x2y2 y4 )dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
2 2 3 |
|
y |
5 |
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Oxy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x y |
|
|
x y |
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
3 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
4 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
5 |
|
|
7 |
|
O |
1 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1 x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
(1 x) x |
|
(1 x) |
|
|
|
|
dx |
|
|
. |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
5 |
|
|
|
180 |
|
Рис. до зад. 11.1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коментар. Оскільки область DOxy |
є трикутником, залишаємось у декартовій |
системі координат. Вибираємо інтегрування вздовж осі Oy (область правильна в обох напрямах.)
11.2. Обчислити |
|
|
x2 y2 z2dxdydz. |
V :x2 y2 z2 z |
|
|
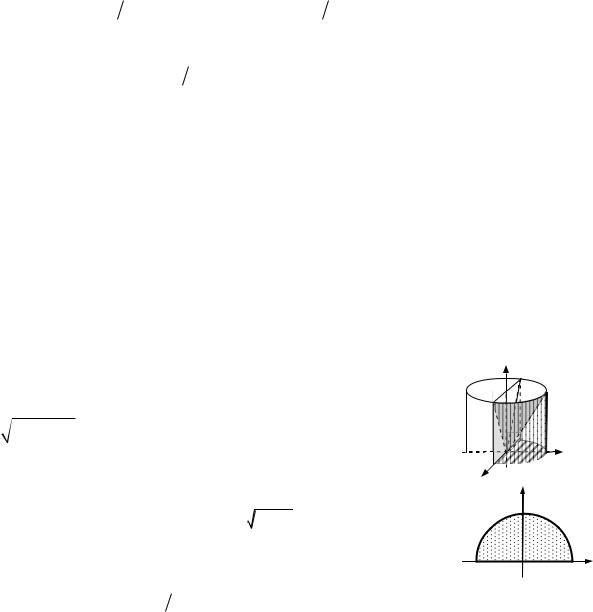
Розв’язання. [2.9.8.]
Оскільки область є кулею, обмеженою сферою x2 y2 z 12 2 14 ,
то інтеграл зручніше обчислювати у сферичній системі координат
[2.1.6]:
|
|
r cos sin , |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r 0, |
|
|
|
|
r sin sin , |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
( ; ], [0; ], |
|
|
r cos , |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
J |
|
r2 sin ; |
x |
|
y |
|
z |
|
r |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[Записуємо рівняння поверхонь у сферичній системі координат.] x2 y2 z2 z; r2 r cos ; r cos .
r cos 0; 0 2 .
.
z
O y
x
Рис. до зад. 11.2
|
|
|
|
|
[2.9.8] |
|
|
x2 |
y2 |
z2dxdydz |
|
r3 sin drd d |
G |
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
2 |
cos |
|
2 |
|
cos |
|
|
d sin r 3d 2 sin r 4 |
d |
|
0 |
0 |
|
|
0 |
4 |
0 |
|
|
|
116 |
Розділ 2. Інтегральне числення функцій кількох змінних |
|
|
2 |
sin d |
cos5 |
|
|
2 |
|
2 |
cos4 |
2 |
5 |
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
Коментар. Від декартових до сферичних координат [2.1.5] у потрійних інтегралів доцільно переходити для областей, обмежених сферами, конусами та площинами, які проходять через вісь Oz.
11.3.1. Знайти об’єм тіла, обмеженого поверхнями y 16 |
|
|
|
|
2x,y 2x, |
z 0,x z 2.
Розв’язання. [2.10.1.]
Об’єм тіла G знаходять за формулою
Тіло G — циліндричне в напрямі осі Oz; на площину Oxy воно проектується в область DOxy, яка є правильною у напрямі осі Oy.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
x 2, |
|
|
|
[2.9.5] |
|
V dxdydz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x y 16 |
|
2x, |
|
|
G |
|
|
|
|
|
|
|
|
|
0 z 2 x |
|
|
|
|
|
|
|
|
|
|
|
|
2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
16 2x |
|
|
|
|
|
2 |
|
|
|
16 2x |
|
|
|
|
|
|
|
|
|
dx |
|
dy dz |
|
dx |
|
|
|
(2 x)dy |
|
0 |
|
2x |
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
2x |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 2 |
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2 x)15 |
2xdx 15 |
2 |
|
2 |
|
x |
|
x |
5 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
5 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
2 |
|
|
|
|
8 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
32. |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z G y
x
y
D
Рис. до зад. 11.3.1
Коментар. Тіло G |
обмежено поверхнями: параболічними |
циліндрами |
|
|
|
|
|
|
твірні яких паралельні осі Oz; площиною Oxy : z 0, |
y 16 2x, y |
|
2x, |
площиною x z |
2, яка паралельна осі Oy. |
|
11.3.2. Знайти об’єм тіла, обмеженого поверхнями 2z x2 y2, z |
2. |
Розв’язання. [2.10.1.] |
|
|
Об’єм тіла G знаходять за формулою |
|
[2.10.1]
V(G) dxdydz.
11. Потрійний інтеграл |
117 |
Тіло G циліндричне в напрямі осі Oz і проектується на площину Oxy в область DOxy, обмежену колом:
|
|
|
2 |
2 |
, |
|
|
|
|
|
|
2z x |
|
y |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
x |
y |
4. |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
[2.9.4] |
|
|
|
|
2 |
|
|
|
G |
V dxdydz |
dxdy |
|
|
|
|
|
|
dz |
|
|
G |
|
|
|
|
DOxy |
x2 y2 |
|
|
x |
2 |
y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
dxdy. |
|
D |
|
|
|
|
|
|
|
|
|
|
Oxy |
|
|
|
|
|
У подвійному інтегралі переходимо до полярних коорди-
нат [2.1.1]:
x2 y2 4; 2 4; 2; 0 2; .
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
Рис. до зад. 11.3.2 |
d |
|
|
2 |
2 |
d 4 . |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
Коментар. Тіло G обмежено поверхнями: параболоїдом 2z |
x2 y2 і |
площиною z 2 0 . |
|
11.3.3. Знайти об’єм тіла, обмеженого поверхнями x2 y2 |
4x, z x, |
z 2x.
Розв’язання. [2.10.1, 2.10.6.]
Об’єм тіла G знаходять за формулою
V(G) dxdydz.
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
Тіло циліндричне в напрямі осі Oz. Проекція D тіла на пло- |
|
z |
щину Oxy є круг x2 y2 |
4x. |
|
|
|
|
|
|
|
Обчислимо інтеграл у циліндричній системі координат |
|
G |
[2.1.3] : |
|
|
|
|
|
|
|
|
|
|
|
|
cos , |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin , |
x |
|
y |
|
|
|
|
|
|
y |
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
z, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
0, ( ; ] |
|
|
|
|
|
|
|
|
|
J |
|
; |
|
|
|
|
|
|
|
x |
4 |
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
[Записуємо рівняння поверхонь у циліндричних координатах.]
118 |
Розділ 2. Інтегральне числення функцій кількох змінних |
|
|
|
|
|
x2 y2 |
4x; |
2 |
4 cos ; |
4 cos . |
|
|
|
|
|
|
|
|
z x; z |
cos ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z 2x; z |
2 cos ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) 4 cos 0; |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[2.9.6] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V(G) dxdydz |
|
d d dz |
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 cos |
2 cos |
|
|
|
4 cos |
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
d |
dz |
|
d |
|
z |2 coscos |
d |
|
|
|
|
2 |
0 |
cos |
|
|
2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
4 cos |
|
|
|
|
2 |
|
|
3 |
|
|
4 cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
2 cos d |
cos |
3 |
|
|
|
|
|
d |
|
|
|
|
2 |
0 |
|
|
|
|
|
|
2 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
[2.3.5] |
|
|
|
2 |
|
|
|
[2.3.8] |
|
|
|
|
|
|
|
|
8 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
64 |
|
|
cos4 |
d |
128 |
|
cos4 d |
128 |
|
3 !! |
|
3 |
|
|
|
|
3 |
|
|
|
|
2 |
|
|
|
|
3 |
|
0 |
|
|
|
|
|
|
|
4 !! |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коментар. Тіло G обмежене коловим циліндром x2 |
y2 |
4x і площина- |
ми z x |
і z 2x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Від декартових до циліндричних координат [2.1.3] у потрійних інтегралах доцільно переходити для областей з осьовою симетрією.
11.3.4. Знайти об’єм тіла, обмеженого поверхнями x2 y2 z2 2Rz.
Розв’язання. [2.10.1.]
Об’єм тіла G знаходять за формулою
V(G) dxdydz.
G
Тіло G обмежено сферами:
x2 y2 z2 R2, x2 y2 (z R)2 R2
і міститься ззовні сфери з центром у точці O. Переходимо до сферичних координат [2.1.5]:
x2 y2 z2 R2,
z
G
y
x
Рис. до зад. 11.3.4
x2 y2 z2 R2; r2 R2; r R; |
|
|
x2 y2 z2 |
2Rz; r2 2Rr cos ; r 2R cos . |
|
|
|
|
|
|
|
r R, |
|
1 |
|
|
|
|
|
cos |
; |
. |
|
|
|
|
r 2R cos ; |
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
.
|
|
|
|
11. Потрійний інтеграл |
|
|
|
|
|
|
|
|
|
|
|
|
|
119 |
|
|
|
|
[2.9.8] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V(G) dxdydz |
r2 sin d d dr |
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
2R cos |
3 |
|
|
|
|
r3 |
|
|
|
2R cos |
|
|
|
|
|
|
|
|
|
|
|
d sin d r2dr |
2 sin |
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
0 |
|
|
R |
|
0 |
|
|
|
|
|
3 |
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 R3 |
3 |
|
|
|
|
|
11 R3 |
|
|
|
|
|
|
|
|
(8 cos 1)sin d |
|
|
|
|
|
|
|
|
. |
|
|
|
|
3 |
|
|
|
12 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.4. Знайти масу тіла G, |
заданого нерівностями |
|
z2 |
x2 |
y2 |
4, |
y, z 0, |
|
64 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
з густиною розподілу маси (x,y, z) |
5(x2 |
|
y2 ) |
. |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
Розв’язання. [2.10.2.] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Масу тіла G з густиною (x,y, z) знаходять за формулою |
|
|
|
|
|
[2.10.2] |
(x,y,z)dxdydz |
|
5(x2 y2) |
|
|
|
m(G) |
|
|
dxdydz. |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
G |
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тіло G — циліндричне в напрямі осі Oz.
Обмежене: знизу площиною z 0, зверху — конусом z 8
 x2 y2 ; і проектується на площину Oxy у півкруг.
x2 y2 ; і проектується на площину Oxy у півкруг.
|
m(G) |
5(x2 |
y2) |
|
|
[2.9.4] |
|
dxdydz |
|
|
4 |
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
8 |
|
x2 y2 |
|
|
|
(x2 |
y2)dxdy |
|
|
dz |
|
|
4 |
D |
|
|
|
|
0 |
|
|
|
|
Oxy |
|
|
|
|
|
|
|
|
10 (x2 y2)3 2dxdy |
[2.7.4] |
|
|
|
|
10 4d d |
|
DOxy |
|
|
|
|
|
|
|
|
|
z
 y x
y x
y
DOxy
Рис. до зад. 11.4
|
2 |
5 |
|
2 |
|
10 d 4d 10 |0 |
5 |
|
0 |
0 |
0 |
|
|
|
Коментар. Тіло G обмежують поверхні: конус z2 64(x2 y2 ) (z 0);
циліндр x2 y2 4 і площини Oxz (y 0) та Oxy (z 0).


 3
3
 2x 0;
2x 0;




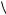
 D
D 



 C
C 





 x
x

 y
y  C
C