Методичка_ОТтаП_Ч1
.pdf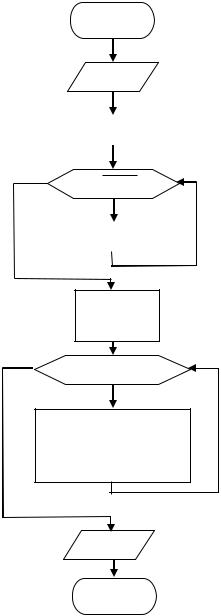
виконуються опеpатоpи тіла циклу (KUKU:=KUKU+I); значення керуючої змінної збільшується на 1.
Цикл завершується при досягненні керуючою змінною свого кінцевого значення (в прикладі - це число 12).
5.5.Приклад
Скласти програму для обчислення суми членів ряду:
|
x |
|
x3 |
x5 |
|||
Z |
|
|
|
|
|
|
... |
(n 1)! |
(n 2)! |
(n 3)! |
|||||
з точністю до члена ряду, що по модулю менше E. Складемо блок-схему алгоритму програми (рис. 5.1) :
Початок
|
x, n |
|
|
|
d := 1 |
|
|
|
i=1, n+1 |
|
Так |
|
|
Ні |
d := d*i |
|
a := x/d i:=0; s:=0
abs(a)>=E
Ні |
Так |
i := i+1 a:=-sqr(x)*a/(n+i+1) s:=s+a
i, a, s
Кінець
Рис. 5.1
60
Тепер запишемо програму:
Program Laba_5; Var
i : integer; {ціла змінна для циклу}
n : integer; {змінна для значення n} d : real;{дійсна змінна для добутку (факторіалу)}
а : real;{дійсна змінна для членів ряду} x : real;{дійсна змінна для значення X} e : real;{дійсна змінна для значення E}
Begin
Write(’Введіть значення X :’);
Readln(x);
Write(’Введіть значення Е :’);{задаємо значення точності}
Readln(е);
Write(’Введіть значення N :’);
Readln(n);
{знаходимо (n+1)!} d :=1;
For i:=1 To n+1 Do d:=d*i;
a:=x/d; {так знаходимо a0}
i:=0; s:=0; {початкове значення i, s} {виконуємо поки модуль a >= E}
While abs(a) >= E Do Begin
i := i + 1; {збільшуємо i на 1}
a := -sqr(x)*a/(n+i+1); {знаходимо ai} s := s+a; {знаходимо si}
End;
Writeln(’i=’, i);
Writeln(’a=’, a:10:6);
Writeln(’s=’, s:10:5);
End.
61
Виконаємо програму для значень X=5.0 і N=4, отримаємо результат:
Введіть значення X : 5.0 Введіть значення N : 4 i=59
a= -0,000006 s= -0,17260
5.6.Порядок виконання роботи.
1.Вибрати індивідуальне завдання. Номер варіанту відповідає номеру студента у списку групи.
2.Ознайомитись із теоретичним матеріалом.
3.Скласти алгоритм для розв’язання завдання.
4.Скласти і відлагодити програму на мові Pascal , яка реалізує введення вихідних даних, розв’язання задачі за допомогою оператора case, виведення результатів у зручній формі на екран.
5.Підготувати звіт по роботі.
5.7.Індивідуальні завдання
Скласти блок-схему алгоритму та написати програму для обчислення нижче приведених прикладів, передбачити захист від ‘зациклювання” програми:
1. Обчислити суму членів ряду: |
|
|
|
|
||||||
|
x |
x2 |
x3 |
|
|
|
|
|||
Z |
|
|
|
|
|
... |
|
|
|
|
( x 1)! |
( x 2)! |
( x 3)! |
|
|
|
|
||||
з точністю до члена ряду, що менше E. |
|
|
|
|
||||||
|
|
|
|
|
n |
2i 1 |
||||
2. Обчислити відрізок ряду: S ( 1)i |
x |
|
|
; |
||||||
i |
|
|
||||||||
|
|
|
|
|
i 0 |
2 |
1 |
|||
|
|
|
|
|
|
|
|
|
||
x = 0,56. Розрахунки припинити, якщо x2i 1 |
|
10 4 . |
||||||||
|
|
|
|
|
|
|
|
|
(2i 1) |
|
62
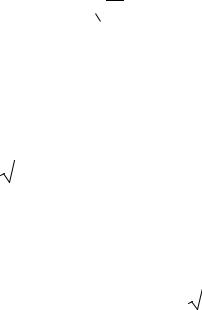
3. Обчислити функцію W 3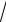
Z , використовуючи ітераційну
|
формулу: W |
W |
|
1 |
( |
|
Z |
W ). |
|||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
n |
|
3 |
W 2 |
n |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
||
|
Розрахунки припинити, якщо |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
W |
|
W |
|
|
10 5; |
W 6; |
Z 220. |
||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
n 1 |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Обчислити y |
|
з точністю E, використовуючи |
|||||||||||||||||||||||||||||||||
4. |
|
x |
|||||||||||||||||||||||||||||||||||
|
співвідношення: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
yi 1 |
|
1 |
( yi |
|
x |
); |
E = 10-3 ; |
x 8,6; y0 = 2,8 . |
|||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
yi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Написати програму обчислення x p |
|
за допомогою |
|||||||||||||||||||||||||||||||||
5. |
|
a |
|||||||||||||||||||||||||||||||||||
|
рекурентного співвідношення Ньютона: x0=a; |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
x |
n 1 |
|
|
|
|
|
|
|
( p 1)x |
n |
|
|
|
|
|
|
|
|
. Точність обчислення: |
||||||||||||||||
|
|
|
|
|
|
|
|
|
p |
1 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
xn 1 xn |
|
|
10 6 . Вихідні дані: p=2; a=3; p=5; a=32. |
||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Знайти значення змінної y |
|
|
|
k 1 k 2 |
|||||||||||||||||||||||||||||||
6. |
|
|
|
|
|
|
|
|
|
для кожного із |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg(x2 1) |
|||||||
значень x, розташованих на інтервалі (-2; 2) з кроком 0,5, з точністю до 0,0001 .
Роздрукувати таблицю значень y і x.
7. Знайти значення змінної y |
|
1 |
з точністю до 0,00001 |
|
|
|
|
||
|
1 |
|
||
|
|
|
||
|
|
|
sin x |
|
|
|
|
||
|
i 1 i2 |
|
|
|
для значень x, розташованих на інтервалі (0; 1) з кроком 0,25. Роздрукувати таблиці значень y і x.
8. Обчислити значення змінної p |
1 |
|
1 |
|
|
|
|
з точністю E |
|
|
(k x) |
|||
|
x2 1 k 1 |
|
||
для значень x, розташованих на інтервалі (-1; 2) з кроком 0,25. Роздрукувати таблицю значень p і x.
63
9. Обчислити суму членів ряду:
z 1 x |
x 2 |
... |
x n |
... |
|
|
|||
2 ! |
|
n! |
|
|
зточністю до члена ряду, що менше E.
10.Обчислити суму членів ряду:
y |
1 |
|
|
|
2 |
... |
n |
... |
|
2 |
3 |
3 4 |
(n 1)(n 2) |
||||||
|
|
|
|
||||||
зточністю до члена ряду, що менше 10-4.
11.Обчислити суму членів ряду:
z cos x |
cos 2x |
|
cos3x |
... |
cos nx |
... |
|
|
n2 |
||||
4 |
9 |
|
|
|||
зточністю до члена ряду, що менше E.
12.Обчислити суму членів ряду:
|
x 1 |
|
( x 1)3 |
|
( x 1)5 |
|
( x 1)2n 1 |
|
||
z 2 |
|
|
|
|
|
|
|
... |
|
... |
|
|
|
|
|||||||
|
|
3( x 1)3 |
|
5( x 1)5 |
|
(2n 1)( x 1)2n 1 |
|
|||
|
x 1 |
|
|
|
|
|||||
зточністю до члена ряду, що менше 10-6.
13.Обчислити суму членів ряду:
z 1 |
mx |
|
|
m(m 1) |
x2 |
|
m(m 1)(m 2) |
x3 |
... |
(m 1)! |
|
|
|||||||
|
|
(m 2)! |
|
(m 3)! |
|
||||
зточністю до члена ряду, що менше 10-4.
14.Обчислити суму членів ряду:
y 1x |
n |
|
1 |
x |
n 1 |
... |
1 |
x |
1 |
|
|
1 |
x |
1 |
... |
|
2 |
|
n |
n 1 |
n 2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
зточністю до члена ряду, що менше 10-6.
15.Обчислити суму членів ряду:
|
mx m m 1 |
|
m m 1 m 2 |
|
|||
z 1 |
m 1 ! |
|
|
x2 |
|
|
x3 |
m 2 |
m 3 ! |
||||||
64
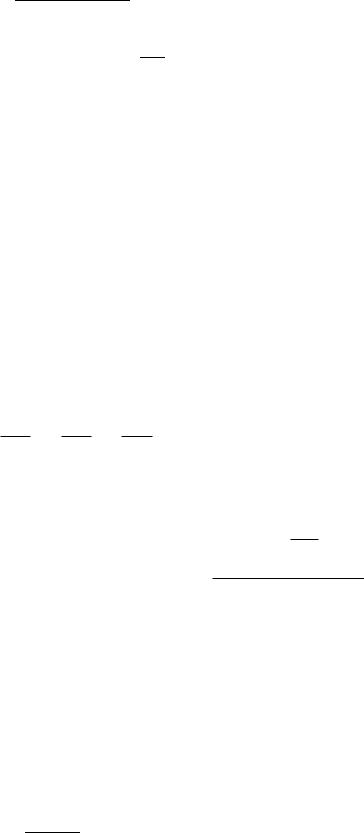
з точністю до члена ряду, що менше E. Для визначеного поточного члена ряду використовувати рекурентну формулу:
yn yn 1 x(m n 1) , де n - номер члена ряду. Початкове
m n
значення y взяти рівним m1!.
16.Обчислити суму членів ряду:
z 1 |
x2 |
|
x4 |
|
x6 |
... |
з точністю до члена ряду, що |
|
|
|
|||||
2 |
4 |
6 |
|
|
|||
менше E.
17.Обчислити число з точністю до десятого знака, якщо
|
4arctg |
1 |
|
arctg |
1 |
. Для обчислення arctg x |
||
|
|
|
|
|
||||
4 |
|
5 |
239 |
|||||
|
|
|
||||||
використовувати наступне розкладання в ряд:
arctg |
1 |
|
1 |
|
1 |
|
1 |
... |
|
x |
x |
3x3 |
5x5 |
||||||
|
|
|
|
|
18.Обчислити суму членів ряду:
z 1 x3 x5 x7 ...
3! 5! 7!
з точністю до члена ряду, що менше E.
1
k 2
19. Знайти значення змінної y k 1 з точністю
cos2 ( x2 0.5)
до 0,00001 для значень x, розташованих на інтервалі (0; 1) з кроком 0,25; на інтервалі (0; 3) з кроком 0,5. Роздрукувати таблицю значень y і x.
20. Знайти методом Ньютона корінь рівняння f (x) ex -
cos(2x)
з точністю до 10-4, взявши як перше приблизне значення кореня x=0. Наступні наближення знаходяться за формулою:
xs 1 xs f ( x) , f '( x)
де f `(x) - похідна від функції f(x).
65
21.Обчислити число за формулою Мечина яка має вигляд:
|
4arctg |
1 |
|
arctg |
1 |
. |
||
|
|
|
|
|
||||
4 |
|
5 |
239 |
|||||
|
|
|
||||||
Для обчислення arctgx використовувати наступне розкладання в ряд:
arctg 1x 1x 31x3 51x5 . Обчислення провести з точністю до шостого знака.
22. Обчислити y 
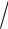x з точністю до четвертого знака, використовуючи співвідношення:
yi 1 |
1 |
( yi |
x |
); x 9,5; |
y0 1,3. |
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
yi |
|
|
|
|
|
||
|
|
|
|
|
|
n |
2i 1 |
||
|
|
|
|
|
|
S 1 i |
x |
|
; |
|
|
|
|
|
|
i |
|
||
23. Обчислити відрізок степеневого ряду. |
i 0 |
2 |
1 |
||||||
|
|
|
|||||||
x=0,56. |
|
|
|
|
|
|
|
||
x2i 1 10 4
Розрахунки припинити, якщо 2i 1 .
24.Обчислити з точністю до п’ятого знака:
|
(x 2)2 |
|
(x 3)3 |
(x 4)4 |
|||
ln x (x 1) |
|
|
|
|
|
... |
|
2 |
3 |
4 |
|||||
|
|
|
|
||||
25. Обчислити значення функції sin y з точністю до п’ятого знака:
y |
x |
; |
1 x 1; sin |
|
|
x |
|
x |
||||||
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
2 |
|
|
1 |
|
( x )3 |
1 |
|
( x )5 |
|
1 |
( x )7 . |
|
||||
|
|
|
|
|
|
|||||||||
|
3! |
2 |
|
|
5! |
2 |
|
7! |
2 |
|
|
|||
66
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
y |
k |
2 |
|
|
|
26. Знайти значення змінної |
k 1 |
|
|
з точністю до 0,0001 |
||
ctg 2 (x2 2) |
||||||
для значень x, розташованих на інтервалі (0; 1.5) з кроком 0,25. Роздрукувати таблиці значень y і x.
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
y |
k |
2 |
|
|
|
27. Знайти значення змінної |
k 1 |
|
|
з точністю до 0,0001 |
||
sin2 (x2 3) |
||||||
для значень x, розташованих на інтервалі (0; 2) з кроком 0,4. Роздрукувати таблицю значень y і x.
28.Обчислити суму членів ряду:
y |
1 |
|
2 |
... |
n |
... |
|
1 4 |
2 5 |
n(n 3) |
|||||
|
|
|
|
з точністю до члена ряду, що менше 10-4.
|
|
|
1 |
|
1 |
|
30. Обчислити значення змінної d |
|
|
|
|
|
з точністю |
|
2 |
|
(k x) |
|||
|
x |
|
1 k 1 |
|
||
до 0,0001, для значень x, розташованих на інтервалі (-1; 2) з кроком 0,25. Роздрукувати таблицю значень d і x.
31.Обчислити суму членів ряду:
z cos x |
cos 2x |
|
|
||
4 |
|
|
з точністю до 0,0001,
(-1; 2) з кроком 0,25.
cos3x ... cos nx ...
9 n2
для значень x, розташованих на інтервалі Роздрукувати таблицю значень z і x.
5.8.Контрольні запитання
1.Опишіть два види циклу For?
2.Як організувати цикл з додатнім кроком?
3.Як організувати цикл з від’ємним кроком?
4.Як працює цикл з передумовою While?
5.Як працює цикл з постумовою Repeat?
6.Як організувати цикл з дрібним кроком?
7.Як працює структура “цикл у циклі”?
8.Які існують можливості виходу за межі циклу?
67
Додаток
Міністерство освіти України
Національний технічний університет України
“Київський політехнічний інститут”
Кафедра автоматизації
енергосистем
З В І Т про виконання завдання
Заняття №______.
по курсу “Обчислювальна техніка та алгоритмічні мови ” Частина 1
( Н а з в а з а н я т т я )
Виконав: |
студент групи |
|
(шифр групи) |
|
(П.І.Б. студента) |
Перевірив: |
(посада) |
|
(П.І.Б. |
|
викладача) |
Київ (рік)
68
на інших аркушах йде виклад за таким планом:
мета роботи;
основні теоретичні відомості по темі;
умова завдання, вибраного відповідно до варіанта;
блок-схема алгоритму вирішення завдання;
надрукована програма на мові Паскаль і результати розрахунків;
аналіз результатів розрахунків та висновки.
69