
Juk_Ilyenko_Moklyachuk_Orlovskiy_DM_praktikum
.pdf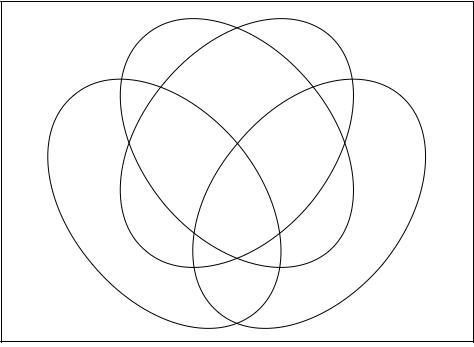
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
0 |
9 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
2 |
0 |
0 |
0 |
1 |
10 |
1 |
0 |
0 |
1 |
3 |
0 |
0 |
1 |
0 |
11 |
1 |
0 |
1 |
0 |
4 |
0 |
0 |
1 |
1 |
12 |
1 |
1 |
1 |
0 |
5 |
0 |
1 |
0 |
0 |
13 |
1 |
1 |
0 |
0 |
6 |
0 |
1 |
0 |
1 |
14 |
1 |
1 |
0 |
1 |
7 |
0 |
1 |
1 |
0 |
15 |
1 |
1 |
1 |
0 |
8 |
0 |
1 |
1 |
1 |
16 |
1 |
1 |
1 |
1 |
5 |
3 |
1 |
|
|
|||
13 |
7 |
|
|
4 |
|
||
9 |
2 |
||
|
|||
12 |
8 |
|
11 |
16 |
6 |
|
15 |
14 |
|
10 |
|
Рис. 2.5.
Будемо мати:
= { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16};
= { 9, 10, 7, 8, 13, 14, 15, 16};
40
= { 5, 6, 7, 8, 13, 14, 15, 16};
= { 3, 4, 7, 8, 11, 12, 15, 16};
= { 2, 4, 6, 8, 10, 12, 14, 16}.
Розглянемо перше рiвняння системи. З огляду на заданий вище спосiб представлення вихiдних множин, будемо мати, що = { 2, 4, 6, 8, 9, 11, 13, 15
= { 5, 6, 13, 14}. Для досягнення рiвностi цих множин необхiдно, щоб множини 2, 4, 5, 8, 9, 11, 14, 15 були порожнiми. Звiдси слiдує,
що
= { 10, 12, 13, 16}, = { 6, 7, 13, 16}, = { 3, 7, 12, 16}, = { 6, 10, 12, 16}.
Розглянемо тепер друге рiвняння системи. Маємо, що ∩ = { 12, 16},
= { 6, 10, 12, 13, 16}. Щоб цi множини спiвпадали, необхiдно, щоб множини 6, 10, 13 були порожнiми. Врахувавши це, будемо мати
= { 12, 16}, = { 7, 16}, = { 3, 7, 12, 16}, = { 12, 16}.
Розглянемо третє рiвняння системи. Так як = { 7}, =
, то для рiвностi цих двух множин необхiдно, щоб множина 7 була порожньою.
Остаточно отримаємо
= { 1, 3, 12, 16}, = { 12, 16}, = { 16}, = { 3, 12, 16}.
Бачимо, що = , .
Перевiримо, що множина = є розв’язком вихiдної системи. Якщо виконано включення , то можна записати
= { }, = { , }, = { , , }, = { , , , }
41

= = { , }, = = ,
= = , ∩ = { , } = .
Як бачимо, всi рiвняння системи виконуються, тобто множина =
є розв’язком вихiдної системи за умови виконання включень.
Задачi для аудиторної та домашньої роботи
№ 2.7. Для унiверсальної множини = {−5, −4, −3, −2, −1, 1, 2, 3, 4, 5}, пiдмножин та унiверсальної множини знайти:
а) ∩ , , , , , , = ( ) ;
б) З’ясувати взаємне розташування множин та ;
в) Знайти ( ) та | ( )|.
1.= {−1, 1, 4, 3}, = { | 4 + 3 − 12 2 − 28 − 16 = 0}
2.= {−1, 1, 2, 3}, = { | 4 + 7 3 + 13 2 − 3 − 18 = 0}
3.= {−1, 1, 3, 4}, = { | 4 − 2 3 − 12 2 + 18 + 27 = 0}
4.= {−1, 1, 2, 3}, = { | 4 − 17 2 + 36 − 20 = 0}
5.= {−2, 1, 3, 4}, = { | 4 − 11 2 − 18 − 8 = 0}
6.= {−1, 1, 4, 5}, = { | 4 + 3 3 − 9 2 − 23 − 12 = 0}
7.= {−3, −1, 1, 2}, = { | 4 − 2 3 − 7 2 + 20 − 12 = 0}
8.= {−4, −1, 1, 2}, = { | 4 − 11 2 + 18 − 8 = 0}
9.= {−2, −1, 3, 5}, = { | 4 + 3 3 − 7 2 − 15 + 18 = 0}
42

10.= {−3, −1, 1, 2}, = { | 4 + 5 3 + 2 − 21 − 18 = 0}
№2.8. Зобразити на координанiй площинi множину , утворену з множин , , .
1.= {( , )| 2 + 2 − 6 ≤ 0}, = {( , )| + 2 + 1 ≥ 0}, =
{( , )|| | ≤ 6, −3 < < −2}, = ( )
2.= {( , )|0 ≤ ≤ √ }, = {( , )|2 ≤ ≤ 6, −3 ≤ ≤ 1},
= {( , )| 2 + 2 − 18 ≤ 0}, = ( )
3.= {( , )| − 2 − 1 ≤ 0}, = {( , )| − 2 + 3 ≥ 0}, =
{( , )| > 0}, = ( )
4. = {( , )| 2 + 2 − 4 ≤ 0}, = {( , )| 2 + 2 + 4 ≤ 0},
= {( , )|| | ≤ 2, | | ≤ 2}, = ( )
5.= {( , )| − 4/ ≤ 0}, = {( , )| 2 + 2 − 25 ≤ 0}, =
{( , )|| | ≤ 1, | | ≤ 1}, = ( ∩ )
6. |
= {( , )| ≤ sin }, = {( , )| > 0, 5}, = {( , )| > −2}, |
||
|
= ( ) ∩ |
||
7. |
= {( , )| − 4 − 1 ≤ 0}, = {( , )|0 ≤ ≤ √ |
|
}, = |
|
|||
|
{( , )| 2 + 2 − 4 ≤ 0}, = ( ∩ ) |
||
8.= {( , )|| | ≤ 5, | | ≤ 1}, = {( , )|| | ≤ 1, | | ≤ 5}, =
{( , )| 2 + 2 ≤ 16}, = ( )
9.= {( , )| 2 − − 2 ≥ 0}, = {( , )| 2 − + 4 ≥ 0}, =
{( , )| > 1}, = ( ∩ )
43

10.= {( , )| 2 + 2 + 6 ≤ 0}, = {( , )| + 2 + 1 ≥ 0}, =
{( , )|| | ≤ 4, −4 ≤ ≤ −2}, = ∩ ( )
№2.9. Чи iснують такi непорожнi множини , та , щоб виконувався наступний набiр умов?
1.= = = , ̸=
2.= = = , ∩ =
3.= ∩ = , ∩ ̸=
4.= = , ̸=
5.∩ = = , =
6.= = = , ̸=
7.= = = , ̸=
8.= ( ) ∩ = , ̸=
9.= ( ) ∩ = , ̸=
10.= = = , ̸=
11.( ) = = = , ̸=
12.= ∩ = , ̸=
13.= = ( ) = , ̸=
14.∩ = = , ̸=
15.= = , ̸=
44
16.∩ = ∩ = = , ∩ ̸=
17.∩ = = , ̸=
18.∩ = ( ) = , ̸=
19.∩ = = , ̸=
№2.10. З’ясувати взаємне розташування множин , ,
1.D = , E = ( ∩ ) ( ∩ )), F = ( ∩ ) ( ∩( ))
2.D = ( ) ( ∩ ), E = , F = ( ) ( ∩ ) ( )
3.D = ( ∩ ) ( ) , E = , F = ( ∩ ) ( ∩ )
4.D = (( ) ) ( ∩ ), E = , F = ( ∩ )
5.D = ( ∩ ) ( ) , E = , F = ( ) ( ∩)
6.D = ( ), E = ( ∩ ) ( ∩ ), F =
7.D = ( ∩ ), E = ( ∩ ) (( ) ), F =
8.D = ( ∩ ) , E = , F = ( ∩ ) ( ∩ ( ))
9.D = ( ∩ ( )), E = ( ∩ ) (( ) ), F =
10.D = ( ∩ ), E = , F = (( ) ) ( ∩ )
45
№2.11. Перевiрити, що включення є необхiдною i достатньою умовою рiвностi
1.= ( )
2.= ( ) (( ) )
3.∩ = ( ) ( )
4.= ( ) ( )
5.= ( ) ( )
6.= ( ) ( ∩ )
7.= ( ∩ )
8.= ( ) ( ∩ )
9.= ( ) (( ∩ ) )
10.= ( )
№2.12. Розв’язати систему спiввiдношень вiдносно множини та вказати умови сумiсностi
1. |
|
∩ = |
|
3. |
|
= |
|
|
|||||||
|
|
|
= |
|
|
|
|
= |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
|
( ) = |
4. |
|
( ) = ∩ |
||||||||||
|
|
|
= |
|
|
|
|
= |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
46
5. |
|
= |
9. |
|
= |
||||||
|
|
|
= |
|
|
∩ |
= |
||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. |
|
= |
10. |
|
= |
||||||
|
|
|
= |
|
|
∩ |
= |
||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7. |
|
= |
11. |
|
∩ = |
||||||
|
|
|
= |
|
|
|
= |
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. |
|
= |
12. |
|
= |
||||||
|
= |
|
|
|
= |
||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ 2.13. Розв’язати систему спiввiдношень вiдносно множини та вка-
зати умови сумiсностi, або довести її несумiснiсть
1. |
|
= ∩ |
3. |
|
∩ = |
||||||||
|
|
∩ |
= |
|
|
|
|
= |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
= |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
|
= |
4. |
|
= |
|||||||
|
|
= |
|
|
|
= |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
= |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
47
|
|
|
|
|
|
|
|
= ∩ |
|||||||||||||||
5. |
= |
8. |
|||||||||||||||||||||
|
|
|
= |
|
|
|
|
|
= |
∩ |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∩ = |
|
|
= |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. |
|
= |
9. |
|
∩ = ∩ |
||||||||||||||||||
|
|
= |
|
|
|
|
= |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∩ = ∩ |
|
|
= |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∩ |
|
|
|
|
|||||||||||||||||
7. |
10. |
∩ = ∩ |
|||||||||||||||||||||
|
|
= |
|
|
|
|
∩ |
= |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
( ) = |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
48
ЗАНЯТТЯ 3
Вiдношення та дiї над ними
Навчальнi задачi
№ 3.1. Для довiльних транзитивних вiдношень = ( , ) та = ( , )
перевiрити, чи буде транзитивним вiдношення .
Розв’язок. Нехай = ( , ), = {( , )}, = {( , )}. Тодi
= {( , )},
= 2{( , )} = {( , ), ( , ), ( , ), ( , ), ( , ), ( , ), ( , ), ( , )}.
Графiк вiдношення мiстить пари ( , ) та ( , ), проте не мiстить пару ( , ), яка є композицiєю двух попереднiх. Тому вiдношення
не є транзитивним.
№ 3.2. Для довiльних рефлексивних вiдношень = ( , ) та = ( , ) перевiрити, чи буде рефлексивним вiдношення .
Розв’язок. Якщо вiдношення заданi на множинi рефлексивнi, це означає, що для кожного елемента множини вiдношення має мiстити пару ( , ). Позначимо = {( , )| } - множина всiх таких пар. Тодi для рефлексивних вiдношень та мають виконуватися умови
та . Проте якщо кожна з цих множин мiстить , то їх об’єднання теж мiстить , тобто . А це автоматично означає, що вiдношення також буде рефлексивним.
49
