
ТЕМА 6. Тертя в мех
..pdf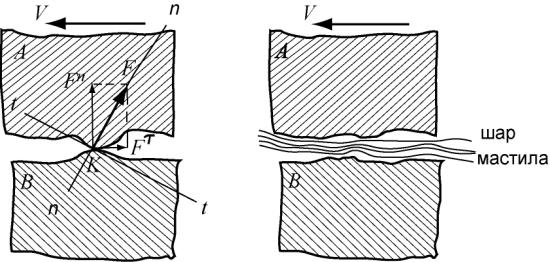
ТЕМА 6. ТЕРТЯ В МЕХАНІЗМАХ
6.1. Види тертя
Питання природи сил тертя до цього часу вивчене недостатньо.
Експериментальні дослідження свідчать, що тертя являє собою складний комплекс механічних, фізичних та хімічних явищ, до того ж ті чи інші явища переважають залежно від умов, за яких відбувається процес тертя.
Розглянемо елементарні відомості з теорії тертя, необхідні для розв'язання найпростіших задач ТММ
Розрізняють два основних види тертя: сухе і рідинне.
Якщо виступаючі нерівності поверхонь А і В (рис. 6.1) безпосередньо стикаються між собою, то такий вид тертя називається сухим.
Якщо між поверхнями А і В є проміжний шар мастила (рис. 6.2) і поверхні А і В безпосередньо не стикаються, то такий вид тертя називається рідинним.
Інколи розрізняють ще два проміжних види тертя: напівсухе
та напіврідинне. |
|
|
|
|
|
Розглянемо схематично ці явища. |
|
|
|||
Якщо |
розглянути |
під |
великим |
збільшенням |
поверхні, |
що труться, |
виявляємо, |
що ці |
поверхні |
не є гладкі, а |
є шорсткі |
та вкриті значною кількістю нерівностей.
Рис. 6.1. Схема сухого тертя Рис. 6.2. Схема рідинного тертя
83
Якщо в точці дотику К (рис. 6.1) прикласти опорні реакції F , спрямовані по нормалі до елементарних площинок дотику,
та розкласти їх на складові |
Fn - |
нормальні і |
F - тангенціальні, |
||||
то нормальні |
складові будуть |
урівноважуватись |
заданими |
||||
нормальними навантаженнями, а тангенціальні складові |
F |
в сумі |
|||||
складуть деяку |
силу опору |
відносному |
переміщенню |
поверхонь |
|||
А і В. Це і буде сила тертя. |
|
|
|
|
|
|
|
За умови рідинного тертя (рис. 6.2) силами тертя будуть сили |
|||||||
опору зсуву окремих шарів мастила. |
|
|
|
|
|||
Напівсухим тертям |
називається |
вид |
тертя, |
за |
якого |
||
найбільш виступаючі шорсткості не розділяються шаром мастила та безпосередньо контактують.
Різниця між напівсухим і напіврідинним тертям головним чином полягає в тому, який з основних видів тертя переважає.
Явища сухого і рідинного тертя за своєю природою зовсім різні, тому різними є і методи урахування сил тертя в механізмах. У фрикційних, пасових та інших передачах спостерігається сухе тертя; у змащених підшипниках, підп'ятниках тощо – рідинне тертя, яке інколи переходить в напівсухе чи навіть сухе (на час пуску машини). Внаслідок цього необхідно вивчати обидва види тертя.
За відносним рухом розрізняють тертя ковзання та тертя кочення.
Тертя ковзання – це зовнішнє тертя за умови відносного ковзання тіл, що стикаються.
Тертя кочення (опір коченню) – це зовнішнє тертя за умови відносного кочення тіл, що стикаються.
6.2.Основні закони тертя ковзання незмащених тіл
6.2.1.Тертя спокою
Розглянемо основні закономірності, що характеризують явище тертя ковзання незмащених тіл.
Нехай тіло, вага якого G, знаходиться в спокої на похилій площині, яка має кут до горизонту (рис. 6.3).
Розкладаємо силу G на нормальну та тангенціальну складові: G cos і G sin ; Fn - нормальна реакція похилої площини; Fтсп -
сила, яка виникає внаслідок тертя, спрямована паралельно площині. Для рівноваги тіла (впливом перекидного моменту нехтуємо)
необхідно, щоб виконувались такі умови:
Fт |
G sin ; Fn G cos . |
(6.1) |
сп |
|
|
84
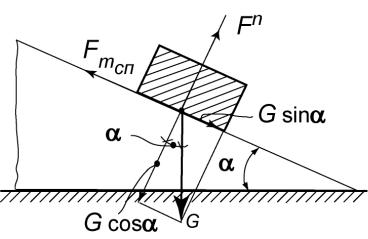
Рис. 6.3. Тертя на похилій площині
із чого випливає:
Fт |
G sin |
|
|
Fn |
|
|
|
сп |
|
|
tg або F |
|
tg . |
(6.2) |
|
|
|
|
|||||
Fn |
G cos |
т |
|
|
|
||
|
сп |
|
|
|
|||
Спостереження показують, що рівновага можлива, поки кут не перебільшує деякого граничного значення сп, де сп- кут тертя
спокою.
tg tg сп. |
(6.3) |
Позначимо:
tg сп |
fcп , |
(6.4) |
де fсп - коефіцієнт тертя спокою. |
|
|
Тоді: |
|
|
tg fсп . |
(6.5) |
|
Сила тертя спокою: |
|
|
F fсп Fn. |
(6.6) |
|
тсп |
|
|
Тертя, яке відбувається за умови відносного |
спокою тіл, |
|
що стикаються, називається |
тертям спокою або |
статичним |
тертям. |
|
|
85
6.2.2. Тертя руху
Якщо тіла, що стикаються, знаходяться у відносному русі, то маємо не тертя спокою, а тертя руху або кінетичне тертя.
На відміну від сили тертя спокою, сила тертя руху виконує певну роботу.
Наприкінці століття французький вчений Кулон опублікував наукову працю, в якій він на основі власних спостережень та досліджень інших вчених (зокрема Амонтона) склав
такі положення:
1. сила тертя ковзання пропорційна нормальному тиску;
2. тертя залежить від матеріалів та стану поверхонь, що труться;
3.тертя майже не залежить від величини відносної швидкості тіл, що труться;
4.тертя не залежить від величини поверхонь дотику тіл, що труться;
5.тертя спокою більш за тертя руху;
6.тертя збільшується із збільшенням часу попереднього контакту поверхонь, що стикаються.
На основі подальших досліджень виявлено, що ці положення Кулона справедливі лише відносно певних матеріалів і в деяких межах зміни швидкостей та навантажень.
6.2.3.Сучасні положення про сили сухого тертя
1.Залежність сил тертя від нормального тиску має такий вигляд (див. рис. 6.4):
F A f |
ков |
Fn , |
(6.7) |
т |
|
|
де А – стала тертя, яка залежить не від тиску, а від здатності до попереднього зчеплення; вона характеризує “причепливість” поверхонь, що стикаються;
fков - коефіцієнт тертя ковзання;
Fn - сила нормального тиску.
Розділимо обидві частини рівняння на Fn :
Fт |
|
A |
fков . |
(6.8) |
|
Fn |
Fn |
||||
|
|
|
86
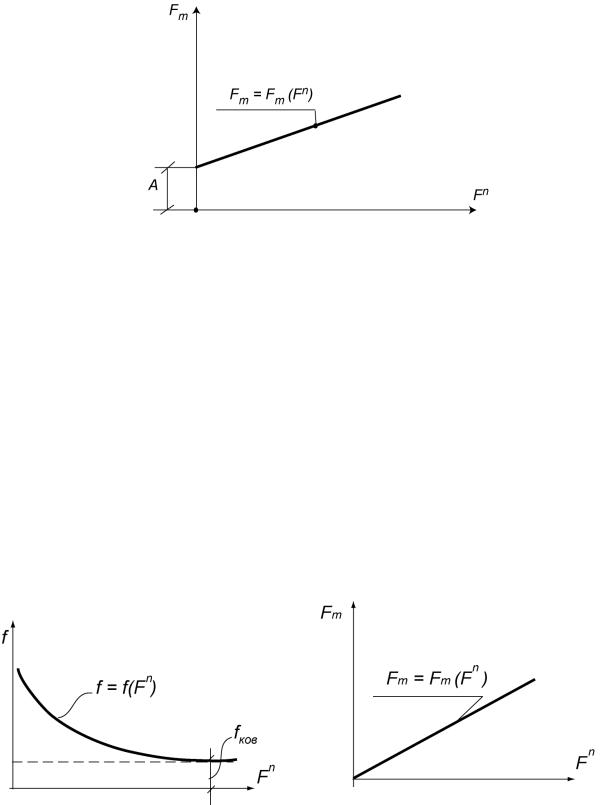
Рис. 6.4. Залежність сили тертя від сили нормального тиску
Але якщо F f Fn , то |
Fт |
f , тоді |
f |
A |
f |
ков |
. |
|
|||||||
т |
Fn |
|
Fn |
|
|||
|
|
|
|
||||
Графік залежності коефіцієнта тертя від сили нормального тиску наведено на рис. 6.5.
На практиці часто “причепливістю” нехтують, користуючись формулою:
F |
f Fn , |
|
|
(6.9) |
|
т |
|
|
|
|
|
тоді графік залежності |
F |
F |
Fn |
має |
вигляд, наведений |
|
т |
т |
|
|
|
на рис. 6.6.
Коефіцієнт тертя f визначається експериментальним шляхом і в розрахунках вважається сталою величиною.
Рис. 6.5. Залежність коефіцієнта |
Рис. 6.6. Розрахункова |
тертя від сили нормального тиску |
залежність сили тертя від сили |
|
нормального тиску |
87
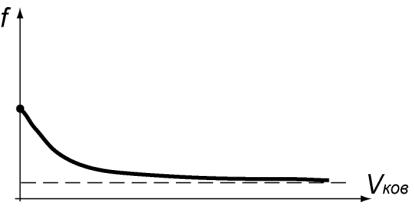
Дослідження показують, що f для більшості матеріалів
зменшується за умови збільшення швидкості ковзання (рис. 6.7), за значних швидкостей f const.
Рис. 6.7. Залежність коефіцієнта тертя від швидкості ковзання
Остаточно положення про сили сухого тертя формулюються таким чином:
1.коефіцієнт тертя можна вважати сталим, а сили тертя прямо пропорційними нормальним лише у певному діапазоні швидкостей та навантажень;
2.сили тертя завжди спрямовані у бік, протилежний відносним швидкостям;
3.тертя спокою в початковий момент руху в більшості випадків дещо більше за тертя руху;
4.із збільшенням швидкості руху сила тертя в більшості випадків зменшується, наближуючись до деякого сталого значення;
5.із підвищенням питомого тиску сила тертя в більшості випадків збільшується;
6.із збільшенням часу попереднього контакту сила тертя збільшується.
6.3.Тертя в кінематичних парах
Вуточнених силових розрахунках механізмів виникає потреба врахування сил тертя в кінематичних парах.
Розглянемо, як визначаються сили тертя в нижчих кінематичних парах: поступальній, обертальній та гвинтовій.
88
6.3.1.Тертя в поступальній парі
6.3.1.1.Умова руху повзуна
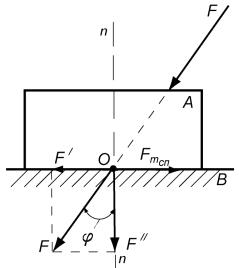
Нехай повзун А навантажений деякою силою F , результуючою всіх сил, що діють на повзун. Також відомі коефіцієнти тертя спокою fсп та ковзання f (рис. 6.8).
Рис. 6.8. До визначення умови руху повзуна
Розглянемо, за яких |
умов |
повзун |
А почне рухатись |
по нерухомій напрямній В. |
Для |
цього |
перенесемо точку |
прикладання сили F в точку О та розкладемо силу F на складові F/ та F// . Кут між напрямом сили F і нормаллю n n позначимо .
Тоді: |
|
F/ F sin . |
(6.10) |
F// F cos . |
(6.11) |
Під дією сили F// поверхні зближуються, а під дією сили F/ повзун намагається зсунутись відносно напрямної.
Сила тертя за Кулоном - Амонтоном:
Fт |
F// |
fсп. |
(6.12) |
сп |
|
|
|
Повзун зсунеться з місця у той момент, коли значення
F |
/ F |
, де F - сила тертя спокою. |
|
т |
т |
|
сп |
сп |
89
Підставимо в рівняння для Fтсп значення F/ і F// :
F sin F cos fсп. |
(6.13) |
Тоді:
fсп |
sin |
tg . |
(6.14) |
|
|||
|
cos |
|
|
Але fсп tg сп , отже, повзун виходить зі стану спокою, коли
сп, де сп- кут тертя спокою.
Із кулонівських положень відомо, що сила тертя руху менша за силу тертя спокою: Fт Fтсп , отже, і кут тертя руху менший за кут
тертя спокою: cп.
6.3.1.2. Геометрична форма зображення взаємодії сил
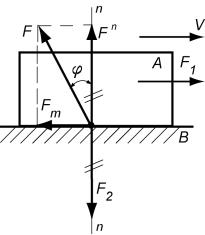
Розглянемо умову рівноваги повзуна А, який рухається по напрямній В зі швидкістю v const (рис. 6.9).
Рис. 6.9. До визначення умови рівноваги повзуна
На повзун діють сили F1 і F2 . Сила F1 прагне зсунути повзун уздовж напрямної В, а F2 притискає повзун до цієї напрямної.
У свою чергу, напрямна В діє на повзун нормальною реакцією Fn та силою тертя Fт. Відомий кут тертя .
Тоді сила тертя: |
|
|
F Fn |
f . |
(6.15) |
т |
|
|
90
Результуючу силу F отримуємо складанням сил Fn і Fт:
F Fn2 |
F2 |
Fn2 |
Fn2 f 2 |
Fn2 |
Fn2 tg2 |
|
|||||||
|
|
|
|
|
т |
|
|
|
|
|
|
(6.16) |
|
|
n |
|
|
|
|
|
n |
1 |
|
|
|
|
|
F |
1 tg |
2 |
F |
|
, |
|
|
||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
cos |
|
|
|
||
звідки: |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
F cos Fn. |
|
|
(6.17) |
||
Отже, |
з цього випливає, що повна реакція F |
відхилена від |
|||||||||||
нормалі n n |
на кут тертя . |
|
|
|
|||||||||
Висновок: Для урахування сил тертя в поступальній парі необхідно відхилити реакцію F від напряму нормалі n n на кут тертя у бік, протилежний напряму швидкості v повзуна відносно напрямної.
Якщо тіло знаходиться в спокої, то реакція F відхилена від нормалі на кут, менший чи рівний куту тертя спокою сп (рис. 6.10).
Рис. 6.10. Кути тертя спокою сп |
Рис. 6.11. До визначення умови |
та руху |
можливості руху повзуна |
6.3.1.3. Умови можливості та неможливості руху повзуна
Покажемо тепер, що коли результуюча зовнішня сила F , яка діє на нерухомий повзун А, прикладена під кутом до нормалі n n, який менший від кута тертя спокою сп, то повзун А не може
рухатись (рис. 6.11).
91
Розкладаємо силу F на дві складові: |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
F/ |
F sin . |
|
|
|
|
(6.18) |
|||||||||
|
|
|
|
|
F// |
F cos . |
|
|
|
|
(6.19) |
|||||||||
Сила тертя спокою: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
F |
|
F// f |
сп |
F cos tg |
сп |
. |
|
|
(6.20) |
||||||||||
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
сп |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Підставимо в цю формулу значення для F через F/ : |
|
|||||||||||||||||||
|
|
|
|
|
F |
F/ |
|
. |
|
|
|
|
|
|
|
|
(6.21) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
sin |
|
|
|
|
|
||||||||
Отже: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fт |
|
F/ |
cos tg сп |
|
F/ |
tg сп |
. |
|
|
|
|
(6.22) |
||||||||
|
|
|
|
|
|
|
|
|||||||||||||
сп |
|
|
|
|
sin |
|
|
|
|
|
|
tg |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
За умовою |
|
сп |
, |
отже, |
|
|
|
tg сп |
1, звідки |
F |
/ F |
, тобто |
||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
tgα |
|
|
|
т |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сп |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
сила, яка прагне зсунути повзун А по напрямній В менша за силу тертя спокою.
Якщо сп, то нерухомий повзун залишається в спокої
незалежно від значення сили F . |
|
||
Повзун починає переміщуватись, коли сп. |
нормалі n n |
||
Відкладаємо кут |
сп |
праворуч та ліворуч від |
|
(див. рис. 6.11). Тоді |
кут |
2 сп буде обмежувати |
деяку область |
рівноваги тіла.
Будь-яка сила, що прикладена в цій області під кутом сп, не може вивести повзун зі стану спокою.
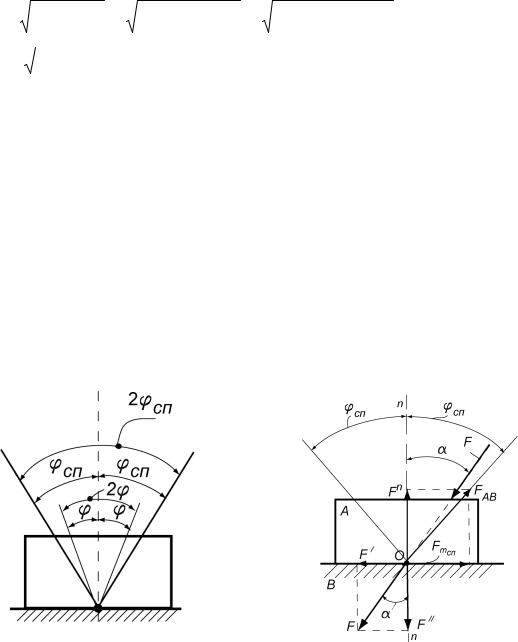
Якщо надавати силі F різні напрями в просторі, область рівноваги буде обмежена конусом тертя спокою (рис. 6.12), який може бути утворений обертанням кута тертя навколо нормалі n n до поверхонь, що дотикаються.
Аналогічно, якщо тіло рухається, то напрям сили F повинен бути по твірній або ж ззовні конуса під кутом 2 сп .
92
