ПриклАкустика-1_2

Лекція 10 Розділ 2. Архітектурна акустика

2.1. Історія розвитку архітектурної акустики

Основи архітектурної акустики були закладені в глибокій старовині, по суті, тоді, коли з'явився театр. Слово "театр" в перекладі з грецької мови означало "місце, щоб бачити". В перших відкритих театрах глядачі розташовувалися на схилах гори, біля підніжжя якої демонструвалися танці. Пізніше з'являється драма, і в поняття "театр" включається поняття "місце, щоб слухати". Це зумовило поступову трансформацію споруди. Оратор або актор знаходиться на піднятому майданчику. Глядачі розміщувалися крутим амфітеатром. Глядацькі місця розташовувалися по колу. Це робилося для максимального наближення глядачів до актора, оскільки через відсутність стін і стелі звукова енергія не підкріплювалася відбиттями і різко зменшувалася при віддаленні від джерела звуку. Репліку актор вимовляв голосно, добре поставленим голосом, поволі, з великими паузами. Потім актори повторювали репліку хором. Актори надягали великі маски, які підкреслювали риси обличчя, біля рота був рупороподібний отвір.

У роботі Вітрувія "Десять книг по архітектурі" узагальнюється досвід античних архітекторів. Побудовані перші променеві картини поширення звуку.

Під лавами глядачів розташовувалися, так звані, "гармоніки" – бронзові посудини, які в сучасному розумінні були системою резонаторів.

В пізніші часи, коли цивілізація розповсюдилася в країнах з помірнішим кліматом, навколо площі, зайнятої глядачами, виникли стіни і стеля. З'явилися багатоярусні балкони. Як "гармоніки" стали використовуватися резонансні властивості поверхонь з дерев'яною обшивкою. Безліч театрів, що збереглися до наших днів, відносяться до шедеврів архітектури і акустики. Проте, проектування тільки на основі досвіду приводило до копіювання будівель, або до пошуків нових рішень, що вимагають десятиліть для знаходження оптимального варіанту.

Вивчення цього питання до середини XIX століття було незначним. Тільки в 1853 році доктор Уфам провів ряд дослідів у великому Бостонському залі (США) і помітив вплив різних оздоблювальних матеріалів на якість звучання в ньому.

Друга половина XIX століття ознаменувалася значним підвищенням інтересу учених до цієї області науки. Разом з тим

1

дослідження ряду учених, в тому числі і Релея, приміщення як тривимірної системи з розподіленими параметрами давали лише якісний аналіз і були непридатні для застосування в інженерній техніці.

Тільки в кінці XIX століття Себіном (США) було виконане перше дослідження, що поклало початок розвитку теорії архітектурної акустики. Не дивлячись на те, що в основу покладені серйозні припущення і ідеалізація процесів, теорія Себіна названа класичною.

У 1895 році ректор Гарвардського університету запропонував Себіну, який у той час був асистентом професора, виявити акустичні дефекти в лекційному залі тільки що побудованого Музею мистецтв в Гарварді. Основним недоліком лекційного залу була його надмірна гулкість. Вимовлене слово звучало протягом 5,5 с через багатократне віддзеркалення від стін, стелі, підлоги.

Час післязвучання, тобто тривалість звучання після виключення джерела Себін назвав часом реверберації, а сам процес післязвучання за рахунок перевідбиття звуку від захищаючих приміщення поверхонь

– реверберацією.

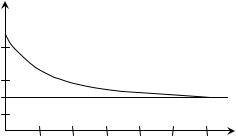
За час 5,5 с той, що говорить, вимовляє 12-15 складів. Тому слухати мову в такому залі важко через погану розбірливість. Себін в першу чергу виміряв час реверберації. Джерелами звуку служили різні органні труби. Він правильно припустив, що ступінь ослаблення реверберації залежить від поглинання звуку. Разом з колегами Себін приніс близько 1500 подушок від сидінь з найближчого театру і поступово заповнював ними сидіння крісел. Результати експерименту представлені на рисунку.

T , c

5

Рис. 2.1

2

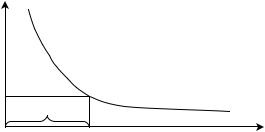
Через 3 роки, в 1898 році, уважно вдивившись в цю криву, Себін помітив, що вона є "хвостом" гіперболи, початок якої зміщено вліво по горизонтальній осі.

Рівняння такої гіперболи має вигляд:

(a x)T K ,

де a – величина зсуву відносно початку координат; x – довжина подушок;

T – час реверберації; K – стала.

T , c

5,5

стіни

Вираз (a x) характеризує повне поглинання звукової енергії

в залі, а величина " a ", яка виявилася рівною 146 м, - поглинання стінами (і іншими захищаючими поверхнями), виміряне в одиницях довжини "стандартної подушки".

Таким чином Себін довів, що повне поглинання звуку в приміщенні, помножене на час реверберації, є величина постійна. До цього дня ця формула є основною в архітектурній акустиці і носить назву формули Себіна.

Зрозуміло, подушка є не кращою одиницею вимірювання поглинання звуку. Тому за одиницю поглинання Себін вибрав поглинання 1 м2 відкритого вікна в припущенні, що вся енергія, що попала на вікно, не повертається (без врахування явища дифракції).

2.2. Теорії архітектурної акустики

Розглянемо звуковий процес в приміщенні. Включаємо джерело звуку: першою до слухача приходить пряма хвиля, а потім хвилі, відбиті від захищаючих поверхонь. При тривалому звучанні джерела

3

наступає усталений режим, тобто загальна енергія в приміщенні буде постійною (поглинена енергія компенсується тою, що поступає від джерела). Якщо джерело включити, спостерігається процес реверберації, тобто поступового згасання перевідбитих хвиль.

Оскільки і мова, і музика є сукупність імпульсних сигналів, то ми їх сприймаємо у вигляді складних процесів наростання і згасання звукової енергії.

Ці процеси в приміщенні строго вивчаються в теорії, названій хвилевою, яка розглядає об'єм приміщення як коливальну систему з певним набором власних частот:

n n c ). l

Таке завдання можна вирішити для приміщень простої форми, але в практичних випадках, в інженерних розрахунках використання хвилевої теорії не раціональне через її складність.

Найдавніша теорія архітектурної акустики – геометрична. Звукова хвиля замінюється звуковим променем, який відображає переважний напрям розповсюдження хвилі. У приміщенні будуються променеві картини, які дозволяють якісно оцінити звукове поле (наприклад, зони тіні або фокусування звуку); знаходяться площадки відбиттів на обмежуючих поверхнях (відбиваючись від цих ділянок стін, стелі та ін., звук потрапляє на площадку із слухачами); оцінюється якість сприйманої програми по ранній ділянці ревербераційного процесу. Теорія придатна для аналізу приміщень неправильної форми, проте, швидше дає якісні результати ніж кількісні.

Найширше застосування в інженерній практиці знайшла теорія, що одержала назву статичної, основоположником якої є Себін.

2.3.Статистична теорія архітектурної акустики

2.3.1.Основні допущення статистичної теорії

1.У будь-якій точці приміщення застосуємо принцип енергетичного підсумовування. Це значить, що величина

4

звукової енергії визначається підсумовуванням середніх значень енергій, принесених в дану точку всіма відбитими хвилями. Таким чином не враховується амплітуда і фаза доданків, тобто ігнорується інтерференційна картина. Це невірно для тонального сигналу, але справедливо для мови і музики.

2.Поле в приміщенні дифузне, тобто в кожну точку поля в одиницю часу приходить достатньо велике число відбиттів з рівноймовірних напрямів, і щільність звукової енергії в будьякій точці однакова.

2.3.2. Середній час і довжина вільного пробігу звукової хвилі

Припущення про дифузність звукового поля дозволяє ввести поняття середньої довжини вільного пробігу променя, тобто середньої відстані між двома послідовними відбиттями.

Нехай в одиницю часу в будь-яку точку приміщення приходить n відбиттів (промені, відповідно, від останнього відбиття пройшли

шлях l1 , l2 , ... ln ). Тоді середній шлях

lñåð l1 l2 ... ln . n

Використовуючи положення теорії ймовірності, можна показати, що для звичайних приміщень

lñåð 4SV ,

де V - об'єм приміщення, ì 3 ;

S - сумарна площа всіх захищаючих приміщення поверхонь, ì 2 . При цьому, час вільного пробігу звукової хвилі, тобто середній

час між двома послідовними відбиттями, визначається як

де c0 – швидкість звуку в повітрі.

Звідси, число відбиттів в одиницю часу

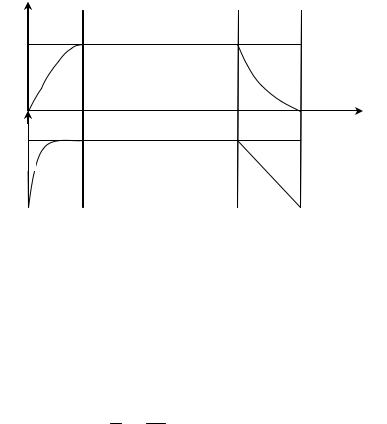
Побудуємо графік залежності W (t) для наростання і спадання звуку в абсолютних одиницях і в дБ:

Вибір логарифмічної шкали нав’язаний тим, що людський слух оцінює гучність (згідно закону Вебера – Фехнера) в логарифмічному масштабі.

w0

L,äÁ

t

0

t

Рис. 2.3

Спостерігається суб'єктивна швидкоплинність процесу наростання рівня звукової енергії, завдяки якій це явище не грає будьякої істотної ролі в оцінці акустичної якості приміщення.

Спадання ж рівня звукової енергії грає дуже важливу роль. Спадання відбувається по похилій прямій, добре фіксується слухом, і може бути досить тривалим процесом:

Нахил прямої визначає швидкість спадання звуку

Lt 4cSV ln 1 10 lg e.

9

2.3.4.Стандартний час реверберації

Заналізу кута нахилу прямої спаду рівня звукової енергії в приміщенні витікає, що час спаду (або час реверберації) залежить від потужності джерела, тобто від рівня звуку в приміщенні.

Щоб використовувати час реверберації як критерій, була введена нормована величина – стандартний час реверберації.

Стандартний час реверберації – це час, протягом якого звукова енергія зменшується в 106 разів, або рівень звукової енергії зменшується на 60 дБ.

Саме ця величина використовується в розрахунках.

Запишемо вираз для спаду звукової енергії від 60 дБ, при цьому час позначимо Т, як стандартний час реверберації:

одержимо формулу для обчислення стандартного часу реверберації:

де V - об'єм приміщення, ì 3 ;

S - сумарна площа захищаючих приміщення поверхонь, ì 2 ;– середній коефіцієнт поглинання звуку в приміщенні.

Ця формула носить назву формули Ейрінга.

Якщо середній коефіцієнт поглинання малий 0.2 , то ln(1 ) і формула спрощується:

де A – сумарний фонд.

Ця формула на згадку про Себіна носить назву формули Себіна. Введена їм закономірність має вигляд:

T A const .

Якщо пригадати, що

A i Si ,

i

то формулу (2) можна переписати:

0,164V T i Si .

i

10