Ряд Фур’є

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный технический университет Украины «Киевский политехнический институт»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

усіх точках неперервності функції f(x)

з інтервалу a;b

сума ряду дорівнює

Зокрема, якщо f(x) визначена лише на інтервалі 0;l

(початок координат

перенесено в точку x a,l

то її можна доозначити на інтервалі

.pdf

Скачиваний:

Добавлен:

12.05.2015

Размер:

270.29 Кб

Скачать

☆

Лекція 11. Розвинення функцій у тригонометричний ряд Фур’є

Короткий зміст Розділ 11.1. Розвинення функцій в ряд

Фур’є 11.1.1. Розвинення в ряд Фур’є парних

та непарних функцій 11.1.2. Ряд Фур’є для неперіодичної

функції Розділ 11.2. Комплексна форма ряду

Фур’є

Короткий зміст

У лекції:

—наведено методи розвинення періодичних функцій в ряд Фур’є;

—розглянуто розвинення неперіодичних функцій в ряд Фур’є;

—виведено комплексну форму ряду Фур’є.

11.1. Розвинення функцій в ряд Фур’є

11.1.1. Розвинення в ряд Фур’є парних та непарних функцій

Нехай f(x) — 2l - періодична парна функція (її графік симетричний

відносно осі Oy). Тоді функції	f(x)sin	n		x, n ,		є непарними функціями, а

всі коефіцієнти			l

1	l		n
bn l	f(x)sin		l		xdx,n ,
	l

дорівнюють нулеві. Отже, ряд Фур’є для парної функції має вигляд:

f x

an cos l

де

n 1

f(x)dx,

(11.1)

an l

f(x)cos

l xdx,n

(11.2)

Розвинення парної 2l - періодичної функції в ряд Фур’є

Висновок.

відбувається тільки за косинусами.

Припустимо, що

на відрізку

l;l

функція

f(x) непарна

(її графік

симетричний щодо

точки O(0;0)).

Тоді функції

f(x)cos

x, n , є

непарними функціями і

an 0,n 0,1,2,...,

bn l

f(x)sin

l xdx,n

(11.3)

sinn x.

f x bn

n 1

Розвинення

непарної 2l - періодичної функції в ряд

Висновок.

Фур’є відбувається тільки за синусами.

Зауваження 11.1.

Приклад 11.1.

 Графік функції

Якщо графік функції f(x) симетричний щодо точки

C(0;c), тоді

	a0		1	l		n
		c,an	0,bn l	f(x)sin		l	xdx,n .
	2	c,an	0,bn l	f(x)sin		l	xdx,n .
Отже				l
Отже	, ряд Фур’є має вигляд

					sinn x.
			f x c bn		sinn x.
				n 1		l
				n 1

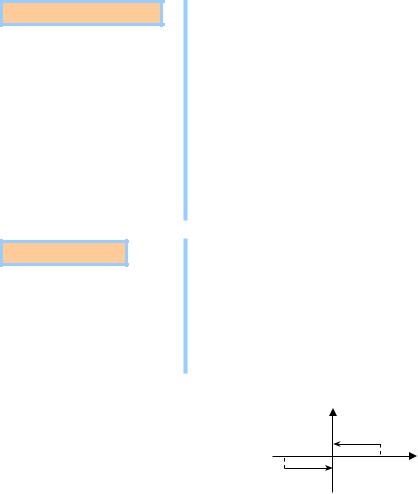
Знайдемо розвинення в ряд Фур’є 2 -періодичної функції f(x):


	1, x 0,

f(x)		1, 0 x .
		1, 0 x .


f(x) на відрізку ;		зображено на рис. 11.1.
y
1
		x
1		x

Рис. 11.1

Функція f(x) на інтервалі ; : має розрив першого роду в точці x 0

(тобто кусково-неперервна), не має екстремумів (тобто кусково-монотонна), обмежена. Отже, вона справджує умови теореми Діріхле і її можна розвинути в ряд Фур’є.

Графік функції симетричний щодо початку координат, отже, ряд Фур’є має вигляд

f(x) bn sinnx.

n 1

Обчислимо коефіцієнти bn за формулою (11.3) l :

cosn 1

1 sinnxdx

cosnx

або, враховуючи , що cosn 1 n :

n 2k,

1 1

,n 2k

1,n .

Отже, сума ряду Фур’є:

sin 2n 1 x

S(x)

;

n 1

2n 1

S(0)

f(0 0) f(0 0)

1 ( 1)

S( ) S( )

f( 0) f( 0)

( 1) 1

Таким чином,

f(x),x

S(x)

0, ,

T 2 .

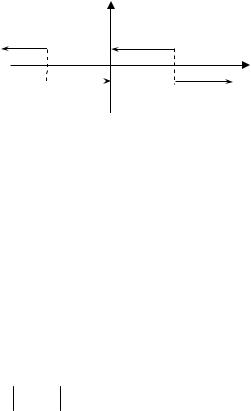
Графік суми ряду Фур’є функції зображений на рис. 11.2 (T 2 ). 

S(x)

Рис. 11.2

11.1.2. Ряд Фур’є для неперіодичної функції

Нехай y f(x)— неперіодична

функція,

яка

задана

на

всій дійсній осі

x . Таку функцію не можна розвинути в ряд Фур’є, оскільки сума ряду Фур’є є періодичною функцією, а тому не може дорівнювати f(x) x .

Але неперіодичну функцію можна розвинути в ряд Фур’є на довільному скінченному проміжку a;b , на якому функція задовольняє умови теореми

Діріхле. Для цього помістимо початок координат в середину відрізка a;b і

розглянемо періодичне продовження функції f(x),x a;b , на всю числову вісь з періодом T 2l b a , вважаючи F(x) f(x), F(x T) F(x).

Ряд Фур’є для періодичного продовження збігається до F(x), причому в

l;0 парним чином і періодично продовжити, покладаючи

	x	0;l		,

f(x),

						F(x 2l) F(x),
F(x) f( x), x l;0 ,						F(x 2l) F(x),

	x 0,
f(0),	x 0,

або непарним чином, тоді
	x		0;l		,
f(x),	x		0;l		,


						F(a 2l) F(x).
F(x) f( x), x l;0 ,						F(a 2l) F(x).

	x 0,
f(0),	x 0,

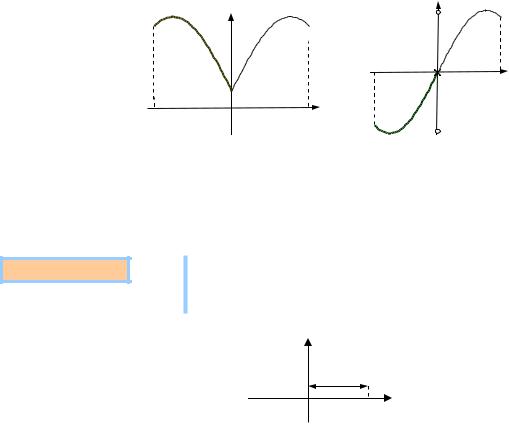
Графік F(x) на l;l буде відповідно симетричним відносно осі Oy або

початку координат (рис. 11.3 а, б):

	y				y
	y
			l		O	l
						x
		x
l	O	l
	а)	Рис. 11.3			б)
		Рис. 11.3
Знаходимо розвинення в		ряд	Фур’є		допоміжної функції F(x) з
періодом 2l . На інтервалі 0;l		дістанемо розвинення функції f(x) в ряд Фур’є,
що містить тільки косинуси або тільки синуси.						0;l , в ряд Фур’є за
Приклад 11.2.	Розвинемо функцію f(x) 1, x					0;l , в ряд Фур’є за
	синусами.
Графік функції f(x) на інтервалі 0;l зображено на рис. 11.4.
		y
		1		x
		0	l	x
		Рис. 11.4
Непарним продовженням f(x) на інтервалі l;0						є функція
			0 x	l,
		1,	0 x	l,

	F(x)		l x	0.
		1,	l x	0.

Продовжимо її періодично з періодом T 2l на всю дійсну вісь. Функція кусково-неперервна, не має екстремумів, обмежена, отже, задовольняє умови теореми Діріхле.

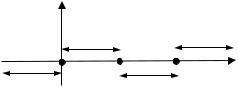
Графік суми ряду Фур’є за синусами, тобто ряду Фур’є функції F(x), зображено на рис. 11.5.

Рис. 11.5

Обчислимо коефіцієнти Фур’є цієї функції:

a0 an 0,n ,

1 sinn l xdx

cosn l x

2k,

0,n

( 1) 1

,n 2k 1,k .

Отже,

4 sin 2n 1 x

S(x)

n 1

S(0) S( l) 0.

Таким чином,

f(x),x 0;l ,

x 0, l,

T 2l.

S(x)

( x),x

l;0

В загальному випадку функцію f(x), яка на проміжку

Зауваження 11.2.

0;l

задовольняє

умови теореми Діріхле, можна

продовжити на проміжок l;0 за допомогою

довільної функції, яка не порушує умови теореми

Діріхле. Отже, функцію,

яка задана на проміжку 0;l ,

нескінченною кількістю способів можна розвинути в

ряд Фур’є. Суми таких рядів Фур’є співпадають з

заданою функцією на проміжку 0;l .

11.2. Комплексна форма ряду Фур’є

Нехай 2 - періодична функція

f(x), x ; , задовольняє умови теореми

Діріхле. Тоді на відрізку

; для неї можна побудувати ряд Фур’є

f(x)

an cosnx sinnx.

n 1

Застосовуючи формули Ейлера:

cos

e i

sin

ei e i

одержимо

einx

e inx

einx

e inx

f(x)

n 1

a ib

neinx

e inx.

n 1

Запровадимо позначення

an ibn

c ,

an ibn

Тоді

f(x) c0

cneinx

c ne inx

n 1

c0 cneinx

cneinx,

тобто

n 1

f(x)

cneinx.

(11.4)

Вираз (11.4) називають комплексною формою ряду Фур’є функції f(x) з

комплексними коефіцієнтами Фур’є cn .

Для коефіцієнтів cn справджуються співвідношення:

f(x)(cosnxdx i sinnx)dx

f(x)e inxdx,n .

(11.5)

2l , тоді комплексна

Якщо функція f(x) задана на відрізку

l;l

форма ряду Фур’є набуває вигляду

f(x)

cnei

l x,

(11.6)

де коефіцієнти cn обчислюються за формулою

f(x)e i l

xdx,n .

(11.7)

Функцію ei l

називають n-ою комплексною гармонікою, отже, ряд (11.2)

описує розвинення функції за комплексними гармоніками.

Зауваження 11.3.

Для

дійсної

функції

f(x) коефіцієнти cn

та c n є

комплексно-спряженими числами c n

b i

отже, модулі коефіцієнтів комплексного ряду Фур’є є

амплітудами відповідних гармонік.

Приклад 11.3.

Знайдемо комплексну форму ряду Фур’є для функції

f(x) x ( x ).

 Маємо

inx

2 ni

cosn

,n 0,

2 ni

xdx 0.

Ряд Фур’є набуває вигляду:

einx

einx,

n 0

причому

x i

einx, x ; ,

S( ) 0.



n 0

Зауваження 11.4. Знаючи комплексні коефіцієнти Фур’є cn , можна знайти відповідні дійсні коефіцієнти Фур’є an та bn за формулами

a20 c0, an 2Recn, bn 2Imcn.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.11.2019434.18 Кб1Руйнування гірських порід.doc
#
17.03.2016297.47 Кб413Руны (Таблица).doc
#
21.08.20197.72 Mб44Руны.docx
#
10.09.201929.04 Кб1русс 13-15 Юля Е.docx
#
12.05.2015249.34 Кб12Рыков поп-арт.doc
#
12.05.2015270.29 Кб50Ряд Фур’є.pdf
#
24.11.201991.25 Кб2с3.docx
#
22.12.201830.58 Кб2сам текст.docx
#
29.07.201953.25 Кб4Сама все знаю.doc
#
17.03.20163.82 Mб13Самогон в большом городе.doc
#
14.11.201977.31 Кб6Самоменеджмент_Тесты.doc