
C _Учебник_МОНУ
.pdfДинамічні структури даних |
479 |
Права гілка вже є, порівнюємо 20 і 25. 20<25, тому викликаємо функцію від лівого піддерева відносно елемента зі значенням 25:
search_insert(root->right->left, 20)
Створюємо новий елемент.
4)Викликаємо для 6: search_insert(root, 6)
Корінь є, тому порівнюємо 6 і 10. Оскільки 6<10, викликаємо цю ж саму функцію для лівого піддерева:
search_insert(root->left, 6)
Створюємо новий елемент.
5)Викликаємо для 21: search_insert(root, 21)
Корінь є, тому порівнюємо 21 і 10. Оскільки 21>10, викликаємо цю ж саму функцію для правого піддерева:
search_insert(root->right, 21)
Права гілка вже є, тому порівнюємо 21 і 25. 21<25, тому викликаємо функцію від лівого піддерева відносно елемента зі значенням 25:
search_insert(root->right->left, 21)
Там вже є елемент зі значенням 20, тому порівнюємо 21 і 20. Оскільки 21>20, тому викликаємо функцію від правого піддерева відносно елемента зі значенням 20:
search_insert(root->right->left->right, 20)
Створюємо новий елемент.
Далі продовжуємо рекурсивно викликати функції від лівого й правого піддерев, допоки не дістанемось кінця гілки (вузол=0 ). Тоді створюємо новий вузол.
Функція пошуку елемента в дереві: int Find(Node *root, int x)
{if (!root) return 0;
else if (root->d==x) return 1;
else if (x < root->d) return Find(root->left, x); else return Find(root->right, x);
}
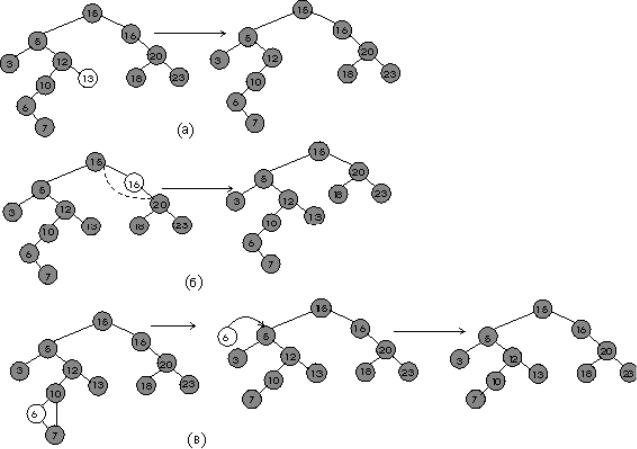
Вилучення вузла з дерева являє собою не таке просте завдання, оскільки вузол, що вилучається, може бути кореневим, містити два (рис. 13.2, в), одне (рис. 13.2, б) чи не містити посилання (рис. 13.2, а) на піддерева. Для вузлів, які містять менше двох посилань, вилучення є тривіальне. Щоб зберегти впорядкованість дерева при вилученні вузла із двома посиланнями, його замінюють на вузол з найближчим до нього ключем. Це може бути крайній лівий вузол його правого піддерева чи то крайній правий вузол лівого піддерева (наприклад, щоб вилучити з дерева на рис. 13.1 вузол із ключем 25, його треба замінити на 21 або 30, вузол 10 замінити на 20 або 8).
Динамічні структури даних |
481 |
if(x > root->d) root->right = Del_el(root->right, x); else
{ P = root;
if (!root->right) |
//Випадок 2: праве піддерево не існує, |
root = root->left; |
//лівий елемент стає на місце root. |
else |
|
if (!root->left) |
//Випадок 2: ліве піддерево не існує, |
root = root->right; |
//правий елемент стає на місце root. |
else |
//Випадок 3: існують два піддерева. |
{ v = root->left; |
//Перехід на лівий вузол, |
while(v->right) |
//проходження праворуч до кінця. |
{P = v; v = v->right;} //P – попередній вузол. |
|
root->d = v->d; |
//Змінювання значення вузла root. |
if(P!=root) |
//Якщо Р дорівнює root, долучення праворуч |
P->right = v->left; |
//елементів з лівого піддерева v |
else P->left=v->left; |
//або долучення їх ліворуч. |
} |
|
//Звільнення пам‟яті від крайнього правого елемента (на який замінено root) delete v;
}
return root;
}
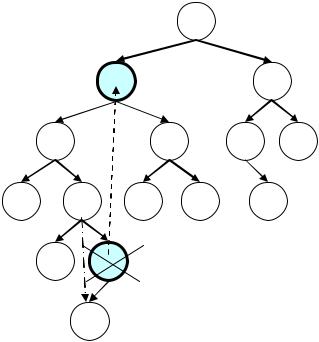
На поданому нижче рисунку схематично зображено вилучення вузла зі значенням 6
|
|
|
10 |
|
|
|
|
root |
|
|
|
|
|
6 |
|
|
25 |
|
root->d=v->d |
|
|
|
|
1 |
|
|
8 |
20 |
30 |
|
|
P |
|
|
|
0 |
3 |
7 |
9 |
|
21 |
v
2 5
P->right=v->left
4
Вузол root має два піддерева. Переходимо на ліве (1). Йдемо лівим піддеревом до крайнього правого елемента (5). Замінюємо значення root (6) на 5. Перш ніж звільнити пам‟ять від елемента зі значенням 5, долучаємо його ліву гілку до попереднього елемента у якості правої гілки.
Динамічні структури даних |
483 |
Node* root=0;
Node * first(char ukr[20], char eng[20])
{Node *pv = new Node; strcpy(pv->ukr, ukr); strcpy(pv->eng, eng); pv->left = 0; pv->right = 0;
return pv;
}
// Пошук з долученням
Node * search_insert(Node *root, char ukr[20], char eng[20])
{if(!root)
{root = new Node; strcpy(root->ukr, ukr);
strcpy(root->eng, eng); root->left=0; root->right=0;
}
else
if(strcmp(ukr, root->ukr)<0) root->left=search_insert(root->left, ukr, eng);
else root->right=search_insert(root->right, ukr, eng); return root;
}
//Пошук слова українською мовою
char* Find(Node *root, char ukr[20])
{if(!root) return v; else
if(strcmp(root->ukr,ukr)==0) //Якщо слово віднайдено,
return root->eng; |
//повертання його англійського перекладу |
else |
|
if(strcmp(ukr,root->ukr)<0) return Find(root->left, ukr);
else
return Find(root->right, ukr);
}
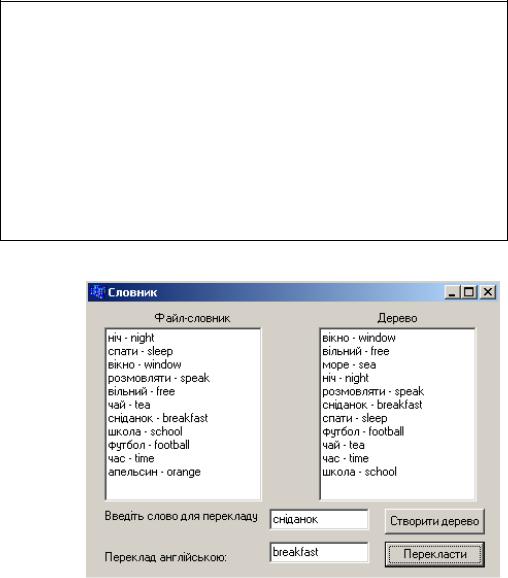
// Виведення слів з дерева до Memo2 (слова відсортовано за алфавітом) void print_tree(Node *p)
{AnsiString S; if(p)
{print_tree(p->left);
S=AnsiString(p->ukr)+" - "+AnsiString(p->eng); Form1->Memo2->Lines->Add(S); print_tree(p->right);
}
}
// Звільнення пам‟яті від дерева void ochistka(Node* p)
{if(p)
{ ochistka(p->left);
Динамічні структури даних |
485 |
1955 р. Джорджем Х. Мілі й 1956 р. Едвардом Ф. Муром. Автомати Мілі та Мура дещо відрізнялися один від одного, але ці відмінності є неістотні. Наведемо означення, більш подібне до автомата Мілі.
Автоматом називається п‟ятірка M = (S, X, Y, F, s0),
де S – непорожня скінчена множина, елементи якої (s1, s2, s3, …) називаються станами автомата;
X – непорожня скінчена множина, яка називається вхідним алфавітом автомата;
Y – непорожня скінчена множина, яка називається вихідним алфавітом автомата;
F – відображення F: S × X → S × Y; s0 – початковий стан автомата.
Кожен автомат має скінчену множину станів. Автомат переходить з одного стану до іншого під впливом послідовності літер вхідного алфавіту. На момент запуску він перебуває у початковому стані s0. На вхід автомата поступає перший елемент вхідної послідовності x1, й відображення перетворює пару (s0, x1) до пари (s1, y1). Елемент s1 стає новим станом автомата, а елемент y1 – першим елементом вихідної послідовності. Отже, автомат перетворює певну вхідну послідовність у вихідну.
Алфавіт автомата – це скінчена множина певних символів. Наприклад, множина {1, 2} – це алфавіт, який складається з одиниці та двійки, множина {A, B, …, Z}– це алфавіт великих латинських літер.
Вхідним алфавітом є скінчена множина допустимих вхідних символів, з якої формуються зчитуванні автоматом рядки. Вихідний алфавіт – це скінчена множина допустимих вихідних символів, з якої формуються рядки-результати. Найпоширенішим є різновид автоматів, коли набори елементів вхідного й вихідного алфавітів автомата збігаються.
За приклад доволі простого автомата розглянемо ліфт у двоповерховому будинку. Припустімо, що цей ліфт вміє реагувати на такі команди:
О – відчинити двері (від англ. open – відчинити);
С – зачинити двері (від англ. close – зачинити);
D – спуститися на перший поверх (від англ. down – донизу);
U – піднятися до другого поверху (від англ. up – догори).
Окрім того, ліфт може виконувати комбінацію вище наведених команд, наприклад: “СUО”, що означає: “зачинити двері”, “піднятися до другого поверху”, “відчинити двері”. Але існують команди, які для такого ліфта будуть некоректними. Приміром, не можна рухатися з відчиненими дверима чи підніматися на другий поверх, коли ліфт уже перебуває на другому поверсі.
Тепер наведемо чотири можливі стани ліфта:
CD – перший поверх, двері зачинено;
OD – перший поверх, двері відчинено;
CU – другий поверх, двері зачинено;
OU – другий поверх, двері відчинено.
Динамічні структури даних |
487 |
першого перетворення автомат змінить стан: зі стану “ОD” дугою “С” здійсниться перехід до стану “СD”. Після другого переходу зі стану “СD” за команди “U” автомат змінить свій стан на “СU”. Після третього переходу за команди “О” автомат перейде до стану “ОU”.
13.7.2 Синхронні автомати
Автомат називають синхронним, якщо він перетворює один елемент вхідного на один елемент вихідного алфавіту.
Програми, що реалізують синхронні автомати, можуть використовувати оператори циклу for для опрацювання послідовності елементів та вкладені в нього оператори switch та if для аналізу й перетворювання елементів.
Розглянемо на прикладі засоби програмування такого автомата.
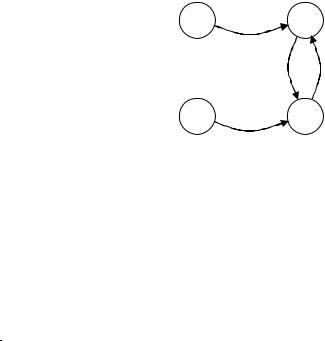
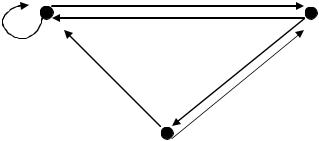
Приклад 13.11 Автомат задано алфавітом X = Y ={0, 1} і трьома станами –
A, B, C:
А |
0/1 |
В |
|
||
|
|
0/0
1/0
1/0
1/1
0/1
С
Ввести вхідну послідовність символів S з алфавітом Х і здобути вихідну послідовність після дії заданого автомата (перетворений рядок S).
Розв‟язок. По дугах автомата можна визначити, наприклад, що в стані А елемент 0 буде перетворено на 1 і при цьому автомат перейде до стану В, а елемент 1 перетвориться на 0 і автомат залишиться у тому ж самому стані А. Аналогічно інтерпретуються інші дуги. Цей автомат, заданий графічно, можна подати також у вигляді таблиці переходів:
Стан |
Вхідний елемент |
||
|
|
||
0 |
1 |
||
|
|||
|
|
|
|
А |
B,1 |
A,0 |
|
|
|
|
|
В |
А,0 |
C,0 |
|
С |
B,1 |
A,1 |
|
|
|
|
|
У наведеній програмі опрацювання вхідної послідовності реалізовано у функції. Зауважимо, що цю функцію можна реалізувати багатьма іншими способами. Стан автомата (А, В чи С) обирається послідовно для кожного з опрацьовуваних символів рядка за допомогою оператора switch.
На вхід автомата подається рядок символів з вхідного алфавіту. Кожен з цих символів буде перетворено згідно до команд переходу, при цьому автомат змінюватиме свій стан. Розглянемо послідовно дії автомата у кожному стані.
Якщо автомат перебуває у стані А можливі дві ситуації: 1) при опрацю-


 OD
OD  CD C
CD C CU
CU