
C _Учебник_МОНУ
.pdf
Динамічні структури даних |
469 |
Функція вставлення нового елемента після елемента с1: void insert_el(Element* c1, int x)
{Element* c=new Element; c->d=x; c->next=c1->next; c1->next=c;
if (c1==last) last=c;
}
Функція вилучення зі списку елемента, який слідує після елемента с1: void del_el(Element* c1)
{Element* c=c1->next; c1->next=c->next;
if(c==first) |
// Якщо вилучається перший елемент, |
first=c->next; |
// першим стає другий |
if(c==last) |
// Якщо вилучається останній елемент, |
last=c1; |
// останнім стає передостанній |
delete c; |
|
}
Функція звільнення пам‟яті від списку: void ochistka()
{Element* c; last->next=0; while(first!=0)
{c=first; first=first->next; delete c;
}
}
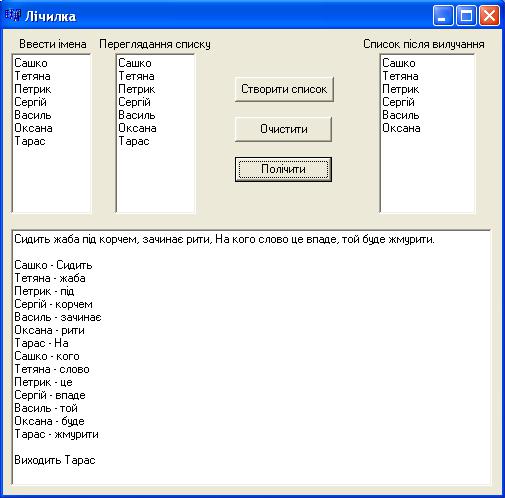
Приклад 13.8 Створити список з іменами хлопчиків та дівчаток. Створити файл з лічилками. Обрати у довільний спосіб одну з лічилок і полічити дітей. Вивести до Memo імена дітей з відповідним словом лічилки. Вилучити зі списку ім‟я того, хто вибув.
Розв‟язок. Оскільки імена дітей під час лічби змінюватимуться циклічно, то список слід обрати однозв‟язний циклічний.
Лічилки запишемо до файла lichilki.txt заздалегідь. У програмі буде згенеровано випадкове число і рядок з цим номером буде зчитано з файла. Саме цей рядок і буде обраною лічилкою. Рядок слід поділити на слова (це можна зробити, приміром, за допомогою функції strtok).
Уміст файла lichilki.txt, створеного у Блокноті:
Ходила квочка коло кілочка. Водила діточок біля квіточок! Квок!
Сітка, вітка, дуб, дубки – поставали козаки. Шабельками брязь – вийди, князь. Сидить жаба під корчем, зачинає рити. На кого слово це впаде, той буде жмурити. Еники-беники їли вареники. Еники-беники, квас: вийшов маленький Тарас.
Динамічні структури даних |
471 |
last=c;
}
// Функція виведення списку до компонента memo void print_el(TMemo* memo)
{memo->Clear(); Element* c=first;
if (first==0) {ShowMessage("Empty"); return;} do{
memo->Lines->Add(AnsiString(c->name)); c=c->next;
}while(c!=first);
}
// Функція вилучення елемента, який слідує після елемента с1 void del_el(Element* c1)
{Element* c=c1->next; c1->next=c->next; if(c==first) first=c->next; if(c==last) last=c1;
delete c;
}
// Функція звільнення пам‟яті й очищення форми void ochistka()
{Element* c;last->next=0; while(first!=0)
{c=first; first=first->next;
delete c;
}
}
// Кнопка “Створити список”
void __fastcall TForm1::Button1Click(TObject *Sender)
{int i, N=Memo1->Lines->Count; for(i=0; i<N; i++)
if(first==0) fir(Memo1->Lines->Strings[i].c_str()); else add_el(Memo1->Lines->Strings[i].c_str());
print_el(Memo2);
}
// Кнопка “Очистити”
void __fastcall TForm1::Button2Click(TObject *Sender)
{ochistka(); print_el(Memo4);
}
// Кнопка “Полічити”
void __fastcall TForm1::Button3Click(TObject *Sender) { randomize();
int n=random(4); // Генерування випадкового числа з проміжку [0,3] int i=0; char s[200];
if((f=fopen(fn, "rt"))==0) {ShowMessage("Can't open file"); return;}
Динамічні структури даних |
473 |
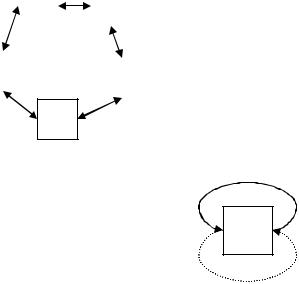
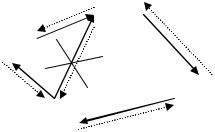
Функція долучення нового елемента до списку (поміж останнім і першим):
void add_el(int x) |
|
|
|
|
first |
||
|
|
|
|
|
|||
{ Element* c=new Element; |
c |
|
|
|
|
|
|
|
|
|
4 |
|
|
||
c->d=x; |
|
|
|
|
|
||
|
|
|
|
|
|
||
c->next=first; |
1 |
|
|
|
|
|
|
c->prev=last; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
last->next=c; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
first->prev=c; |
|
|
|
|
|
|
-5 |
last=c; |
|
0 |
|
|
|
||
|
|
|
|
|
|||
} |
|
|
|
|
|
||
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Функція виведення списку до Memo від |
|
|
last |
||||
першого елемента до останнього: void print_beg(TMemo* memo)
{memo->Clear(); Element* c=first;
if(first==0) {ShowMessage ("Порожній"); return;}
do{ memo->Lines->Add(IntToStr(c->d)); c=c->next;
}while(c!=first);
}
Функція виведення списку до Memo від останнього елемента до першого: void print_end(TMemo* memo)
{memo->Clear(); Element* c=last;
if(last==0) { ShowMessage ("Порожній"); return;} do{ memo->Lines->Add(IntToStr(c->d));
c=c->prev;
} while(c!=last);
}
Функція вставлення нового елемента після елемента с1: void insert_el(Element* c1, int x)
{Element* c=new Element; c->d=x; c->next=c1->next; c1->next->prev=c; c1->next=c; c->prev=c1; if(c1==last) last=c;
}
Функція вилучення зі списку елемента, який слідує після елемента с1:
void del_el(Element* c1) { Element* c=c1->next;
c1->next=c->next; c->next->prev=c1; if(c==first) first=c->next; if(c==last) last=c1;
Динамічні структури даних |
475 |
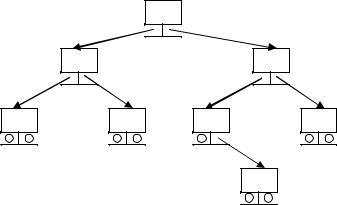
Якщо для кожного вузла дерева всі ключі його лівого піддерева є менше за ключ цього вузла, а всі ключі його правого піддерева – більше, то воно називається деревом пошуку. У такому дереві однакові ключі заборонено. У дереві пошуку можна віднайти елемент за ключем, рухаючись від кореня й переходячи на ліве чи то праве піддерево залежно від значення ключа в кожному вузлі.
Дерево є рекурсивною структурою даних, оскільки кожне піддерево також є деревом. Дії з такими структурами найоптимальніш описуються за допомогою рекурсивних алгоритмів. Приміром, функцію обходу всіх вузлів дерева у загальному вигляді можна описати як
void way_around (<дерево>)
{way_around (<ліве піддерево>) <відвідування кореня>
way_around (<праве піддерево>)
}
Можна обходити дерево й у іншому порядку, наприклад, спочатку корінь, потім піддерева, але наведена функція дозволяє одержати на виході відсортовану послідовність ключів, оскільки спочатку відвідуються вершини з меншими ключами, розташовані у лівому піддереві. Результат обходу дерева, зображеного на рис. 13.1:
1, 6, 8, 10, 20, 21, 25, 30
Якщо у функції обходу перше звертання іде до правого піддерева, результат обходу буде іншим:
30, 25, 21, 20, 10, 8, 6, 1
Отже, дерева пошуку можна застосовувати для швидкого сортування та пошуку значень. При обході дерева вузли не вилучаються.
Для бінарних дерев визначені такі операції:
вилучення вузла до дерева;
пошук по дереву;
обхід дерева;
вилучення вузла.
Для кожного рекурсивного алгоритму можна створити його нерекурсивний еквівалент.
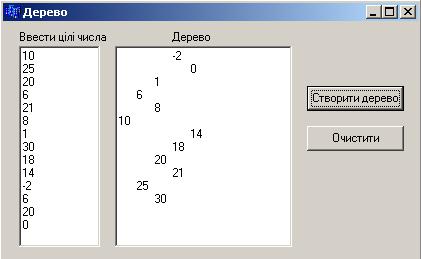
Приклад 13.9 Увести цілі числа до Memo і сформувати з них дерево пошуку.
Розв‟язок. У програмі реалізуємо нерекурсивну функцію пошуку по дереву із включенням і рекурсивну функцію обходу дерева.
Перша функція здійснює пошук елемента із заданим ключем. Якщо елемент знайдено, вона повертає вказівник на нього (елементи з однаковими ключами у дереві пошуку заборонено), а якщо елемента немає – включає його у відповідне місце дерева і повертає вказівник на нього. Для включення елемента слід пам‟ятати пройдений деревом шлях на один крок назад і знати, чи виконується включення нового елемента в ліве чи праве піддерево його предка.
Динамічні структури даних |
477 |
// Допоки в дереві є елементи і елемент зі значенням х не знайдено while(pv && !found)
{prev = pv;
if(x==pv->d) found = true;
else |
|
// Якщо значення вузла не збігається з х |
if(x<pv->d) |
|
// і, якщо х є менше за значення вузла, |
pv = pv->left; |
// перехід до лівого піддерева, |
|
else pv = pv->right;// або перехід до правого піддерева. |
||
} |
|
|
if(found) |
// Якщо вузол зі значенням х було знайдено, |
|
return pv; |
//повертання вказівника на нього |
|
Node *pnew = new Node; |
// Створення нового вузла |
|
pnew->d = x; |
|
|
pnew->left = 0; |
|
|
pnew->right = 0; |
|
|
if(x<prev->d) |
|
|
prev->left = pnew; |
// Долучення до лівого піддерева предка |
|
else |
|
|
prev->right = pnew; |
//Долучення до правого піддерева предка |
|
return pnew; |
|
//Повертання вказівника на новий вузол |
}
// Виведення дерева – рекурсивна функція void print_tree(Node *p, int level) { AnsiString S="";
if(p)
{ print_tree(p->left, level+1); |
//Виведення лівого піддерева |
|
for(int i=0; i<level; i++) S=S+" |
"; |
|
S=S+IntToStr(p->d); |
|
|
Form1->Memo2->Lines->Add(S); |
//Виведення кореня піддерева |
|
print_tree(p->right, level +1); //Виведення правого піддерева
}
}
void ochistka(Node* p) { if(p)
{ ochistka(p->left); ochistka(p->right); delete p;
}
else return;
}
// Кнопка “Створити дерево”
void __fastcall TForm1::Button1Click(TObject *Sender) {int i, N=Memo1->Lines->Count;
for(i=0; i<N; i++)
if(root==0) root=first(StrToInt(Memo1->Lines->Strings[i])); else search_insert(root, StrToInt(Memo1->Lines->Strings[i])); print_tree(root, 0);
}
//-------------------------------------------------------------
