C _Учебник_МОНУ

Якщо розглядати цю послідовність, розпочинаючи від молодших членів до старших, спосіб її побудови задається циклічним алгоритмом, а якщо, навпаки, – від заданого n=n0, то спосіб визначення цього елемента через попередні буде рекурсивним.

Вочевидь, що рекурсія не може бути безумовною, бо у такому разі вона стає нескінченною. Про це свідчить принаймні наведена вище лічилка. Рекур-

сія повинна мати всередині себе умову завершення, за якою наступний крок рекурсії вже не виконуватиметься.

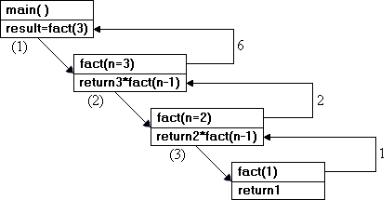
Рекурсивні функції лише на перший погляд схожі на звичайні фрагменти програм. Щоб відчути специфіку рекурсивної функції, варто простежити за текстом програми перебіг її виконування. У звичайній програмі будемо йти ланцюжком викликів функцій, але жодного разу повторно не увійдемо до того самого фрагменту, допоки з нього не вийшли. Можна стверджувати, що перебіг виконування програми “лягає” однозначно на текст програми. Інша річ – рекурсія. Якщо спробувати відстежити за текстом програми перебіг її виконування, то дістанемось такої ситуації: увійшовши до рекурсивної функції, “рухаємося” її текстом доти, допоки не зустрінемо її виклик (можливо, з іншими параметрами), після чого знову розпочнемо виконувати ту ж саму функцію спочатку. При цьому слід зазначити найважливішу властивість рекурсивної функції: її перший виклик ще не завершився. Чисто зовні складається враження, що текст функції відтворюється (копіюється) щоразу, коли функція сама себе викликає. Насправді цей ефект відтворюється в комп‟ютері. Однак копіюється при цьому не весь текст функції (не вся функція), а лише її частини, пов‟язані з локальними даними (формальні, фактичні параметри, локальні змінні й точка повертання). Алгоритмічна частина (оператори, вирази) рекурсивної функції й глобальні змінні не змінюються, тому вони присутні в пам‟яті комп‟ютера в єдиному екземплярі.

Кожний рекурсивний виклик породжує новий “екземпляр” формальних параметрів і локальних змінних, причому старий “екземпляр” не знищується, а зберігається у стеку на засаді вкладеності як “матрьошки”. Тут має місце єдиний випадок, коли одному імені змінної в перебігу роботи програми відповідають кілька її екземплярів. Відбувається це в такій послідовності:

у стеку резервується місце для формальних параметрів, куди записуються значення фактичних параметрів. Зазвичай це виконується в порядку, зворотному до їхнього місця у списку;

при виклику функції до стека записується точка повертання – адреса тієї частини програми, де міститься виклик функції;

на початку тіла функції у стеку резервується місце для локальних (автоматичних) змінних.

Зазначені змінні створюють групу (фрейм стека). Стек “пам‟ятає історію” рекурсивних викликів у вигляді послідовності (ланцюжка) таких фреймів. Програма у кожний конкретний момент працює з останнім викликом і з останнім фреймом. По завершенні рекурсії програма повертається до попередньої версії рекурсивної функції й до попереднього фрейму у стеку.

Послідовність рекурсивних викликів можна прокоментувати приблизно

такою фразою: “Функція F виконує ... і викликає F, яка виконує ... і викликає F...”.

При створюванні рекурсивної функції завжди слід добре поміркувати, чи ефективно є застосовувати рекурсивний алгоритм, оскільки рекурсія з надто великою кількістю вкладених викликів може вичерпати ресурси оперативної пам‟яті, що спричинить збій у роботі операційної системи.

Розглянемо алгоритм нераціонального використання рекурсії на прикладі обчислення чисел Фібоначчі – числового ряду, в якому кожен наступний член є сумою двох попередніх: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 і т.д. Італійський математик середньовіччя Леонардо Фібоначчі відкрив цю числову послідовність, вивчаючи піраміду Хеопса у Гізі. До речі, ці числа пов‟язані поміж собою цікавими співвідношеннями. Наприклад, кожне число є приблизно в 1.618 разів більше попереднього (цю пропорцію називають золотою), у 2.618 рази більше того, яке розташоване через одне число від нього і в 4.236 разів більше числа, розміщеного двома числами раніш, а кожне попереднє число складає приблизно 0.618 від наступного. Поширеність співвідношень Фібоначчі у житті просто вражає. Принцип золотого перетину – найвищий прояв структурної й функціональної довершеності цілого та його частин у мистецтві, науці, техніці й природі. Закономірності “золотої” симетрії проявляються в енергетичних переходах елементарних часток, у будові деяких хімічних сполук, у планетарних і космічних системах, у генних структурах живих організмів, у принципах формотворення рослин тощо. Ці закономірності, виявлено як у будові окремих органів людини, так і тіла у цілому, а також вони проявляються у біоритмах і функціонуванні головного мозку і зорового сприйняття.

Ітераційна функція обчислення чисел Фібоначчі має вигляд

long fib1(int n)

{ long a=0, b=1, c=n; for(int i=2; i<=n; i++)

{ c=a+b; a=b; b=c; } return c;

}

Рекурсивна функція матиме вигляд long fib2(int n)

{if(n==0 || n==1) return n;

else return fib2(n-1)+fib2(n-2); }

або

long fib3(int n)

{ return (n>1) ? fib3(n-1)+fib3(n-2) : n; }

Така рекурсивна функція є придатна для використання лише для невеликих значень n, оскільки кожне звертання призводить до двох подальших викликів, причому викликів з одним і тим самим значенням параметра, тобто кількість викликів зростає експоненціально. Отже, у цьому завданні доцільніше застосовувати ітераційну функцію fib1.

Рекурсивні функції найчастіше застосовують для компактної реалізації рекурсивних алгоритмів, а також для роботи зі структурами даних, описаними рекурсивно, наприклад з бінарними деревами. Кожну рекурсивну функцію можна реалізувати без застосування рекурсії. Достоїнством рекурсії є компактний

Приклад 8.15 Написати рекурсивну функцію, яка обчислює мінімальний елемент масиву.

Розв‟язок. Створимо рекурсивну функцію minimum(), яка повертатиме індекс мінімального елемента. Вона матиме три параметри: 1) вказівник на початок масиву mas, 2) розмір масиву n і 3) індекс елемента, з якого розпочинається підмасив. Цей підмасив рекурсивно зменшується, допоки його розмір не становитиме 1. Коли у ньому залишиться один елемент (k==n-1), повертається значення k. На наступному кроці рекурсивного повертання порівнюються mas[k] (останній елемент) та mas[a] (передостанній елемент) та повертається індекс меншого з них. Продовжуючи, на кожному кроці порівнюються мінімум, здобутий на попередніх кроках, і mas[a] (поточний елемент).

Тексти функції та її виклику в основній пр ограмі: int minimum(int *mas, int n, int k)

{if(k == n-1) return k;

int a = minimum(mas,n,k+1);// Виклик для підмасиву розміром на 1 менше

if(mas[a]<mas[k]) return a; else return k;

min = minimum(mas,n,0);// Виклик для всього масиву (k=0). cout<<"Мінімум: mas["<<min<<"] = "<<mas[min]<<endl; getch();

return 0;

}

Приклад 8.16 Написати рекурсивну функцію, яка обчислює суму квадратних коренів натуральних чисел від 1 до n.

Тексти функції та її виклику в основній пр ограмі:

#include <iostream.h> #include <conio.h> #include <math.h> double sumkor(int a)

{if (a==1) return 1;

else return (sqrt(a) + sumkor(a-1));

}

void main()

{int n;

cout<<"n= "; cin>>n; cout<<sumkor(n);

getch(); return 0;

}

delete []s1;

}

void __fastcall TForm1::Button1Click(TObject *Sender)

{AnsiString ss = Edit1->Text; char *s = new char [ss.Length()]; strcpy(s,ss.c_str());

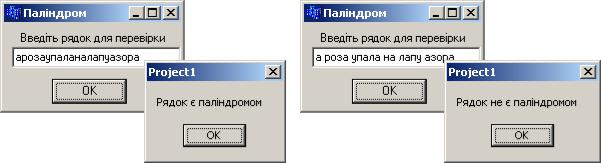
int p = pal(s);

if(p)ShowMessage("Рядок є паліндромом"); else ShowMessage("Рядок не є паліндромом");

}

Зверніть увагу на команду: l=(s[0]==s[strlen(s)-1]);

У ній спочатку виконується порівняння s[0]==s[strlen(s)-1], а потім його результат (true чи false) перетворюється на ціле число (відповідно 1 чи 0) і присвоюється змінній l.

Запис

return l && pal(s1);

означає, що після обчислення pal(s1) обчислюється результат операції логічного множення && і цей результат повертається у точку виклику функції.

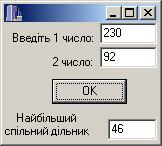
Приклад 8.19 Увести два числа й обчислити найбільший спільний дільник (НСД) двох цілих чисел, застосовуючи рекурсивний алгоритм Евкліда.

Розв‟язок. Нерекурсивна реалізація алгоритму Евкліда обчислення НДС двох цілих чисел наведена у п. 4.4.4.

Тексти функції та основної пр ограми:

int nod(int a, int b) { int c;

// За умови b>a параметри змінюються місцями if(b > a) c = nod(b, a);

else

if(b == 0) c = a;

else c = nod(b, a%b); // Тут a%b – залишок від ділення a на b return c;

}

void __fastcall TForm1::Button1Click(TObject *Sender)

{int a, b;

a = StrToInt(Edit1->Text); b = StrToInt(Edit2->Text);

Edit3->Text = IntToStr(nod(a, b));

}

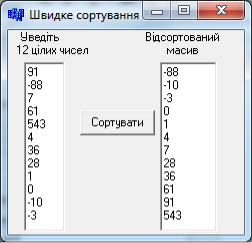
Приклад 8.20 Увести масив з 12-ти цілих чисел і упорядкувати їх за зростанням методом швидкого сортування за допомогою рекурсивної функції.

Розв‟язок. Швидке сортування (англ. quicksort), часто зване qsort на ім‟я реалізації в стандартній бібліотеці мови С – широко відомий алгоритм сорту-

if ( i <= j )

{y=a[i]; a[i]=a[j]; a[j]=y; i++; j--;

}} while (i <= j);

if (L < j) QuickSort(a, L, j); if (i < R) QuickSort(a, i, R); return;

}

void __fastcall TForm1::Button1Click(TObject *Sender)

{int i, a[12];

for (i=0; i<12; i++) a[i]=StrToInt(Memo1->Lines->Strings[i]);

QuickSort(a, 0, 11 ); // На вході ліва і права межа сортування

Memo2->Clear();

for (i=0; i<12; i++) Memo2->Lines->Add(IntToStr(a[i]));

}

8.6 Перевантаження функцій

Часто буває зручно, щоб функції, які реалізовують однаковий алгоритм для різних типів даних, мали однакове ім‟я. Якщо це ім‟я несе певну інформацію, це робить програму більш зрозумілою, оскільки для кожної дії треба пам‟ятати лише одне ім‟я. Використовування кількох функцій з однаковим ім‟ям, але з різними типами параметрів називається перевантаженням функцій.

Компілятор визначає, яку саме функцію слід викликати, за типом фактичних параметрів. Цей процес називається дозволом перевантаження (переклад з англійського слова “resolution”). Тип значення, яке повертає функція, у дозволі не бере участі. Механізм дозволу ґрунтується на доволі складному наборі правил, зміст яких зводиться до того, щоб використати функцію з найбільш придатними аргументами й видати повідомлення, якщо така не віднайдеться. Мета перевантаження – зробити так, щоб функції з однаковим ім‟ям виконувалися по-різному (і за можливість повертали різні значення) при звертанні до них з різними за типами й кількістю параметрами. За приклад наведемо чотири варіанти функції для визначення максимального значення:

int max(int, int); // Повертає найбільше з двох цілих

char* max(char*, char*);//Повертає рядок максимальної довжини