
Metod_LR_TEK1_2014p
.pdf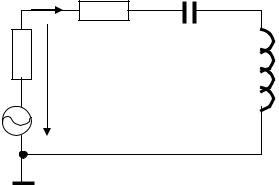
21
Лабораторна робота № 6
Дослідження послідовного коливального контуру (резонанс напруг) Стислий зміст роботи
Впроцесі виконання роботи досліджуються і вивчаються наступні питання:
1)Явище резонансу, яке виникає в нерозгалуженому ланцюгу, що містить в собі котушку індуктивності і конденсатор (послідовний коливальний контур);
2)Умова виникнення резонансу в ланцюгу і його перевірка в лабораторних умовах;
3)Методика виміру резонансних характеристик;
4)Аналітичні співвідношення при резонансі і їх експериментальна перевірка.
Підготовка до роботи
1. При підготовці до роботи необхідно ознайомитися з методичними вказівками, робочим завданням, вивчити зазначені питання до лабораторної роботи по навчальній літературі, зробити всі розрахунки, зазначені цьому розділі та в робочому завданні та відповісти на наступні питання:
а) що розуміють під явищем резонансу і при яких умовах він виникає?
б) зміною яких параметрів можна досягти резонансу в послідовному контурі? в) чому явище резонансу в послідовному контурі називають резонансом напруг? г) які енергетичні процеси виникають в контурі при резонансі?
д) чому дорівнює опір послідовного коливального контуру при резонансі?
е) що називають хвильовим опором, добротністю, загасанням резонансного контуру і узагальненою розстройкою?
ж) як змінюється повна, активна і реактивна потужність, яку споживає послідовний коливальний контур при зміні частоти в діапазоні, що включає резонансну частоту?
з) дайте визначення, характеризуйте вид і призначення узагальненої резонансної характеристики послідовного резонансного контуру.
2. Скласти протокол звіту лабораторної роботи у відповідності з варіантом завдання. Розрахувати теоретично резонансні криві для напруг на елементах ланцюга, які будуть отримані практично в п.3 робочого завдання. Побудуйте також теоретичні графічні залежності цих резонансних кривих (для кожного з випадків а), б), в).
При теоретичних розрахунках спочатку потрібно обчислити резонансну частоту контуру, його добротність Q і визначити значення смуги пропускання контуру 2 f для приведених схем. Тоді діапазон зміни частоти f при розрахунку резонансної кривої буде:
f0-5 f ≤f ≤f0+5 f тобто частота f буде змінюватися в районі f0 з відхиленням (± 5 f/ f0)*100%. Аналогічно розраховується при розрахунках резонансних кривих діапазон зміни параметра контуру L або C. Так ці параметри будуть змінюватися в районі значень, приведених в варіанті завдання з відхиленням:
для L/ L0 або С/С0 → ±.( 1/(1±(5 f/ f0))2-1)
Обчислені в цьому пункті зміни параметрів повинні бути використані при виконанні робочого завдання.
Робоче завдання
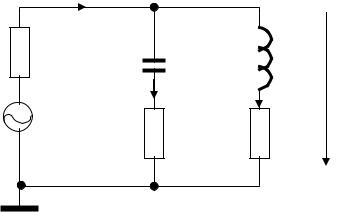
1. Зібрати схему ланцюга послідовного контуру згідно рис.6.1 і у відповідності з варіантом завдання, наведеним в табл.6.2.
I |
|
|
RВН |
R |
C |
U |
|
L |
e
Рис. 6.1
22
2.Встановити значення частоти синусоїдального ідеального генератора (e), що дорівнює резонансній частоті ланцюга f0. Вихідну напругу генератора задати 1 В.
3.Моделюючи ланцюг в часової області, зробити виміри величин, зазначених в таблиці 6.1, для наступних трьох випадків:
а) при незмінній ємності С, у відповідності з варіантом завдання, частотою генератора fо, варіюючи в можливих межах індуктивність котушки L;
б) при незмінній індуктивності L, в відповідності с варіантом завдання, частоті генератора fо, варіюючи в можливих межах ємність конденсатора С;
в) при незмінній ємності С, індуктивності L, у відповідності з варіантом завдання, змінюючи частоту генератора f.
4.За даним п.3 побудувати для кожного з випадків а),б),в) графічні залежності для резонансних
кривих ( на одному графіку I, UL,UC, ϕ - для кожного з випадків), обчислити добротність контуру і його смугу пропускання, порівняти їх значення з отриманим в п.2 робочого завдання. За даними п.3- б) побудувати в масштабі векторні діаграми напруг на елементах ланцюга для випадків: C<C0;C=C0;C>C0 (C0-резонансне значення)
5. Встановити внутрішній опір генератора RВН:
1) RВН=R; 2) RВН=0,1*R.
и провести вимір величин, зазначених в табл. 6.1 для кожного з випадків 1),2) тільки в залежності от частоти f, при значених L,C, відповідних варіантові завдання.
Табл. 6.1 Парам.1____=_______( L/C/f), Парам.2____=______( L/C/f), Змін. параметр_____
Знач. |
|
|
|
|
|
|
|
|
Вар. |
U |
UL |
UC |
I |
ϕ |
P |
Q |
S |
Парам. (напр. |
|
|
|
між |
активн |
реакт. |
повна |
|
L/C/f |
на |
|
|
|
U--I |
. |
|
|
(____) конт.) |
|
|
|
|
|
|
|
|
|
роз екс |
роз екс |
роз екс |
роз екс |
роз екс |
роз екс |
роз екс |
роз екс |
1_____
……
10____
6. За даними п.5 побудувати резонансні криві, наклавши їх на наявні графіки, побудовані в п.4. 7.Визначити та перевірити практично умови узгодження на змінному струмі генератора та контуру для випадку ємності в контурі – C=1.01*C0 при резонансній частоті генератора fо та інших параметрах контуру по вихідному варіанту і обґрунтувати розрахунком правильність отриманих результатів.
8. Зробити висновки і узагальнення по виконаній роботі.
Методичні вказівки
Резонансними або коливальними ланцюгами називаються електричні ланцюги, в яких можуть виникати явища резонансу напруг або струмів.
При впливі гармонійного струму або напруги на пасивний електричний ланцюг, який містить резистори котушки індуктивності і конденсатори, спостерігається режим, при якому її вхідний реактивний опір дорівнює нулю. Такий режим називається резонансом. Для цього режиму характерно те, що реактивна потужність на вхідних затискачах ланцюга виявляється рівною нулю і вся електрична енергія, що надходить в ланцюг від джерела, перетвориться в теплоту.
Резонанс напруг спостерігається в електричному ланцюгу з послідовним з'єднанням ділянок, що містять індуктивності і ємності. Нерозгалужений ланцюг, що складається з послідовно з'єднаних елементів R, С и L (рис.6.2), є одним з найпростіших випадків такого ланцюга. Його називають
послідовним коливальним контуром.
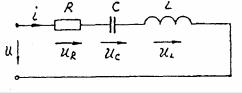 Рис.6.2
Рис.6.2
Якщо в ланцюзі тече синусоїдальний струм i=Imsinωt, то миттєві напруги на елементах ланцюга можна визначити: UR=RImsinωt; UL=Ldi/dt=ωLImsin(ωt+π/2)=XL Imsin(ωt+π/2);
23
1
UC=1/C ∫idt = ωC Imsin(ωt-π/2)=XCImsin(ωt-π/2).
Значення миттєвої напруги на елементах ланцюга:
U=UR+UL+UC= RImsinωt+j(XL-XC) Imcosωt=  R 2 +(X L − X C )2 Imsin(ωt+ϕ);
R 2 +(X L − X C )2 Imsin(ωt+ϕ);
де: ϕ=arctg( X L − X C ) – кут зсуву фази між струмом і напругоюв ланцюгу.
R
Активна P, реактивна S , повна Q, потужності, які споживаються ланцюгом, можуть бути визначені: P=UIcosϕ=I2R; Q= UIsinϕ=I2(XL-XC); S=UI= P 2 +Q 2 =I2  R3 +(X L − X C )2 ,
R3 +(X L − X C )2 ,
де U=Um /  2 ; I=Im /
2 ; I=Im /  2 – діючі амплітуди струмів і напруг на зовнішніх виводах ланцюга.
2 – діючі амплітуди струмів і напруг на зовнішніх виводах ланцюга.
Умова резонансу для такого ланцюга: XВХ=ωL-1/ωC=0.
Резонанс може бути отриманий шляхом зміни однієї з трьох змінних ω, L, C, при незмінних двох інших, значення яких для ланцюга при резонансі повинні задовольняти співвідношення:
ω0=1/ L0 C0 , де ω0=1/2πf0 – кругова резонансна частота, L0, C0 – номінальні значення елементів ланцюга при резонансі.
Повний опір ланцюга при резонансі напруг: Z= R2 + (X L − X C )2 =R – мінімальний і дорівнює
активному опорові. При цьому струм і споживана активна потужність досягають найбільших значень.
Якщо реактивні опори XL=ωL і XC=1/ωC при резонансі перевищують по величині опір R, то напруга на затискачах котушки і конденсатора також буде більше напрузі на опорі R, що дорівнює вхідній напрузі генератора. Тому резонанс в послідовному контурі називається резонансом напруг.
Перевищення напруг має місце, якщо R<ω0L=1/ω0C=  L / C =ρ.
L / C =ρ.
Тут ρ має розмірність опору, чисельно дорівнює опорові реактивного елемента при резонансі і носить назву характеристичного (хвильового) опору контуру.
Вираз Q=UC0/U=UL0/U=I0ω0L0/I0R=ω0L0/R=ρ/R – визначає кратність перевищення напруги на котушці індуктивності або конденсаторі над напругою вхідного генератора і називається
добротністю контуру.
Величина, зворотна добротності, називається загасанням: α=1/Q.
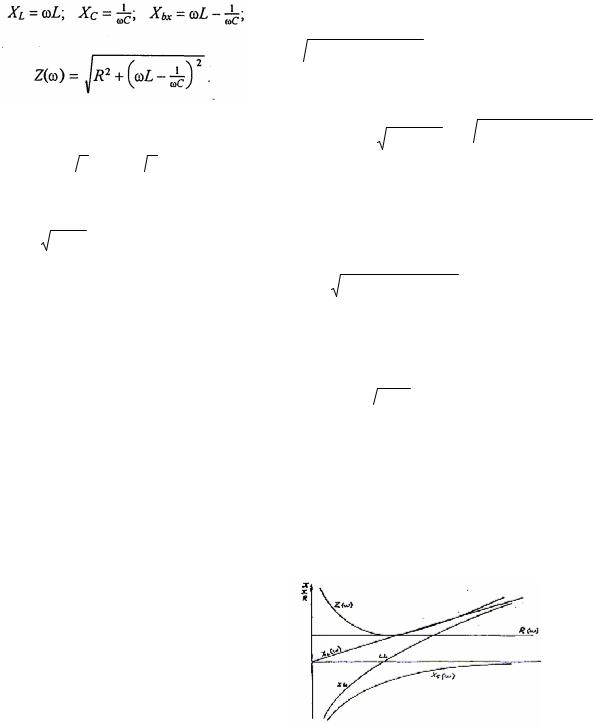
Залежності величин (R ,Xi.,Xc, Zвх) від частоти, що характеризують поведінку ланцюга при зміні частоти вхідного сигналу - називають частотними характеристиками, а залежності діючих значень струму і напруг (або їх відношень) на елементах від частоти - резонансними кривими. На рис.6.З зображені частотні характеристики послідовного контуру, побудовані у відповідності з виразами:
|
Рис.6.3 |
X L − X C |
|
|
|
|
|||
В теорії контурів вводиться поняття іншої частотної змінної ξ = |
. При резонансі ξ = 0 , |
|||
|
||||
|
|
R |
||
тому цю частотну змінну називають узагальненою частотною розстройкою контуру. При використанні узагальненої частотної розстройки контуру ξ будуються нормовані резонансні криві
(нормовані значення струму або напруги на елементі ланцюга по відношенню до його значення при резонансі). Наприклад:
- вираз для комплексного вхідного опору послідовного контуру:
Z ВХ |
= |
|
|
R |
= R |
1 |
−i |
|
ξR |
1 |
+iξ |
1+iξ 2 |
|
+iξ 2 |
|||||
|
|
|
1 |
||||||
- вираз для нормованої резонансної кривої напруги на реактивному елементі контуру:

|
|
|
|
24 |
|
U m |
= |
1 |
де: Um0 |
–амплітудне значення напруги на реактивному елементі при резонансі.. |
|
U m0 |
1+ξ 2 |
||||
|
|
|
Має місце технічний інтерес - умова узгодження на змінному струмі, коли від генератора передається активна максимальна потужність в електричний ланцюг (в даному випадку резонансний контур). У відповідності з рис.6.4 для комплексних амплітуд струму і напруги на навантаженні:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
− |
|
|
|
|
||||
|
|
|
|
|
|
− |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z Г |
|
|
|
I |
|
|
|
|
||||||
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
− |
|
|
E |
− |
|
E Z Н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
I |
= |
|
|
; U Н |
= |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
− |
− |
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Z Г +Z Н |
|
|
Z Г |
|
+ Z Н |
|
|
|
|
|
е |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
− |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
_ |
|
|
|
|
|
|
|
|
|
|
|
Z Н |
U Н |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
− − |
|
|
|
|
|
|
|
|
Рис.6.4 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
+ jX Н ) |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
E E Z Н |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
− * |
|
|
|
|
= |
|
|
|
|
Em (RН |
|
|
|
|
||||||||||||||||||
Повна потужність: |
S =U I = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
− |
− |
|
− |
− |
2 (RГ + RН ) |
2 |
+(X Г + X |
Н ) |
2 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(Z Г +Z Н )(Z Г |
+Z Н )* |
|
|
|
|
|
|
|
|
|||||||||||||||||||
Активна потужність: P= |
1 |
|
|
|
|
Em2 RН |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2 (RГ + RН )2 |
+(X Г + X Н )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Для нашого ланцюга : RГ+RН= RВН+R, |
|
XГ+XН=(ωL-1/ωC). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Тоді умова передачі максимальної потужності в резонансний ланцюг: (ωL-1/ωC)=0, RВН=R, при цій |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E 2 |
|
|
|
|
||||
умові повного узгодження одержимо потужність в ланцюзі: |
P max |
|
= |
m |
. |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Н |
|
|
|
8RВН |
|
|
|
|
||||
Таблиця 6.2 |
|
|
|
|
|
|
Варіанти завдань. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Варіант |
R |
|
Ом |
|
|
|
|
C |
нФ |
|
|
|
|
|
|
|
|
|
L мкГн |
|
|
|
RВН Ом |
|||||||||||||
|
|
|
1 |
|
0.3 |
|
|
|
|
|
|
|
|
1000 |
|
|
|
|
|
|
|
|
|
|
1000 |
|
|
|
|
|
|
|
|
|
|
0.1 |
|||
|
|
|
2 |
|
1.0 |
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
500 |
|
|
|
|
|
|
|
|
|
|
|
0.3 |
||
|
|
|
3 |
|
0.7 |
|
|
|
|
|
|
|
|
500 |
|
|
|
|
|
|
|
|
|
|
1000 |
|
|
|
|
|
|
|
|
|
|
0.2 |
|||
|
|
|
4 |
|
0.3 |
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
|
|
|
|
0.2 |
|
|
|
|
5 |
|
0.5 |
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
250 |
|
|
|
|
|
|
|
|
|
|
|
0.2 |
||
|
|
|
6 |
|
0.8 |
|
|
|
|
|
|
|
|
250 |
|
|
|
|
|
|
|
|
|
|
1000 |
|
|
|
|
|
|
|
|
|
|
0.3 |
|||
|
|
|
7 |
|
0.5 |
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
200 |
|
|
|
|
|
|
|
|
|
|
|
0.2 |
||
|
|
|
8 |
|
0.3 |
|
|
|
|
|
|
|
|
300 |
|
|
|
|
|
|
|
|
|
|
500 |
|
|
|
|
|
|
|
|
|
|
|
0.1 |
||
|
|
|
9 |
|
1.3 |
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
|
300 |
|
|
|
|
|
|
|
|
|
|
|
0.9 |
|
|
|
|
10 |
|
0.5 |
|
|
|
|
|
|
|
|
150 |
|
|
|
|
|
|
|
|
|
|
400 |
|
|
|
|
|
|
|
|
|
|
|
0.2 |
||
25
Лабораторна робота №7
Дослідження паралельного коливального контуру (резонанс струмів)
Стислий зміст роботи
В процесі виконання роботи досліджуються і вивчаються наступні питання:
1)Явище резонансу, яке виникає в паралельному контурі, що містить котушку індуктивності і конденсатор;
2)Умова виникнення резонансу в паралельному контурі і його перевірка в лабораторних умовах;
3)Резонансні характеристики ланцюга і їх особливості;
4)Перевірка аналітичних співвідношень при резонансі .
Підготовка до роботи
1.При підготовці до роботи необхідно ознайомитися з методичними вказівками, робочим завданням, вивчити зазначені питання до лабораторної роботи по навчальній літературі, зробити всі розрахунки, зазначені цьому розділі та в робочому завданні та відповісти на наступні питання:
а) що розуміють під явищем резонансу?
б) зміною яких параметрів можна досягти резонансу в паралельному контурі? в) чому явище резонансу в паралельному контурі називають резонансом струмів? г) які енергетичні процеси відбуваються в контурі при резонансі?
д) як визначити резонансну частоту ідеального і реального паралельних контурів?
е) що називають хвильовою провідністю, добротністю, узагальненою розстройкою і затуханням паралельного контуру?
ж) як визначити резонансний стан ланцюга по величині струмів і напруг на елементах ланцюга? з) наведіть приклади і дайте характеристику параметрів часткового включення паралельного контуру; е) як визначається навантажена добротність паралельного контуру, в тому числі з урахуванням
часткового включення контуру.
2.Скласти протокол звіту лабораторної роботи у відповідності з варіантом завдання. Розрахувати резонансні криві для змінних струмів, які будуть отримані практично в п.3 робочого завдання, а також побудувати теоретичні графічні залежності цих резонансних кривих (для кожного з випадків а), б), в) – на одному графіку всі залежності для струмів та напруг див. табл. 7.1). При цьому потрібно розрахувати ( див. п.2 к ЛР №6 розділ «Підготовка до роботи») резонансну частоту
контуру f0, його навантажену добротність Qен, і діапазони зміни величин f, L, C для побудови резонансних кривих і досліджень контуру в розділі робочого завдання.
Робоче завдання
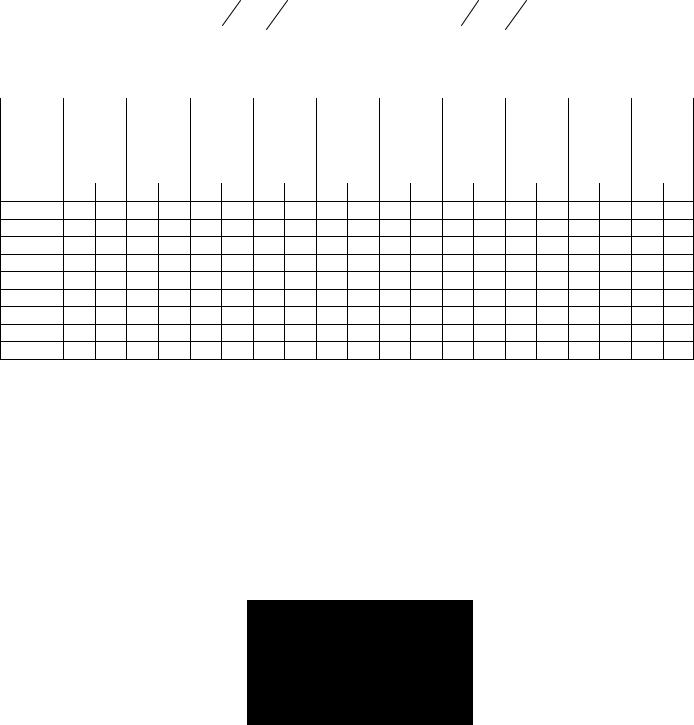
1. Зібрати схему ланцюга паралельного контуру відповідно рис.7.1.
I
RВН |
|
|
|
|
C |
L |
|
+ |
IC |
IL |
U |
E _ |
RC |
RL |
|
Рис.7.1
2. Встановити значення частоти гармонічного генератора Е рівним резонансній частоті ланцюга f0. Вихідну напругу генератора встановити 100 В.
3. В паралельному контурі (див. рис. 7.1 і варіант завдання табл. 7.2 ), зробити виміри часових залежностей і записати в протокол величини, вказані в таблиці 7.1, для наступних трьох випадків:
26
а) при незмінній ємності С, у відповідності з варіантом завдання, частоті генератора fо, варіюючи в можливих межах індуктивність котушки L;
б) при незмінній індуктивності L, у відповідності з варіантом завдання, частоті генератора fо, варіюючи в можливих межах ємність конденсатора С;
в) при незмінній ємності С, індуктивності L, у відповідності з варіантом завдання, змінюючи частоту генератора f.
4.. За даними п.3 побудувати резонансні криві (на одному графічному полі) I, IL, IC, ϕ для кожного з випадків а),б),в), обчислити добротність контуру і його смугу пропускання, порівняти їх значення з отриманим в п.2 розділу «Підготовка до роботи» використовуючи ці графічні залежності. За даними п.3-б) побудувати в масштабі сумісні векторні діаграми напруг та струмів на елементах ланцюга RВН,L,C для випадків: C<C0;C=C0;C>C0 (C0-резонансне значення)
5. Встановити внутрішній опір генератора RВН:
2) RВН= L C *( 1(RL + RC ) ); 2) RВН=0,1 L C *( 1(RL + RC ) );
і провести виміри величин, які вказані в табл. 7.1 для кожного з випадків 1),2) - при значеннях L,C, відповідних варіанту завдання тільки в залежності от частоти f.
Табл. 7.1 Парам.1___=_____( L/C/f), Парам.2___=_____( L/C/f), Вар. параметр __________
Знач. |
|
|
|
|
|
|
|
|
|
|
Вар. |
U |
IL |
IC |
I |
ϕC |
ϕL |
ϕ |
P |
Q |
S |
Парам. (напр. |
|
|
|
між |
між |
між |
активн |
реакт. |
повна |
|
L/C/f |
на |
|
|
|
U—IC |
U—IL |
U--I |
. |
|
|
(____) конт.) |
|
|
|
|
|
|
|
|
|
|
|
роз екс |
роз екс |
роз екс |
роз екс |
роз екс |
роз екс |
роз екс |
роз екс |
роз екс |
роз екс |
1
2
3
4
5
6
7
8
9 6. За даними п.5 побудувати резонансні криві, наклавши їх на наявні теоретичні графіки,
побудовані по п.4.
7.Визначити та перевірити практично умови узгодження на змінному струмі генератора та контуру для випадку індуктивності в контурі – L=1.01*L0 при резонансній частоті генератора fо та інших параметрах контуру по вихідному варіанту і обґрунтувати розрахунком правильність отриманих результатів (див. методичні вказівки до ЛР №6).
8. Зробити висновки і узагальнення по виконаній роботі.
Методичні вказівки
Для виявлення характерних особливостей резонансних режимів в електричних ланцюгах синусоїдального струму належить, попередньо, ознайомитися з методичними вказівками до лабораторної роботи № 6.
Резонанс струмів спостерігається в електричному ланцюзі з паралельним з'єднанням котушки індуктивності і конденсатора рис.7.2. У випадку, якщо R1=0 і R2=0, то ланцюг розглядається як ідеальний резонансний контур.
Рис.7.2

27
Резонанс в ланцюзі (рис. 7.2) настає, якщо вхідна реактивна провідність дорівнює нулю:
BВХ=BC-BL=0
Постановка реактивних провідностей BC і BL, виражених через параметри ланцюга на змінному струмі приводить до рівняння:
ωL / (R12+(ωL)2) – (1/ωC) / (R22+(1/ωC )2) = 0;
Таким чином, резонанс в даному ланцюзі, може бути досягнуто зміною одного з параметрів (ω, L, C, R1, R2) при інших чотирьох постійних. Розв’язок останнього рівняння відносно ω дає наступне значення для резонансній частоти:
ω0= |
1 L / C − R12 |
= |
1 |
ρ2 |
−R12 |
; |
|
LC L / C − R22 |
LC |
ρ2 |
−R22 |
||||
|
|
|
При резонансі рівні і протилежні по фазі реактивні складові струмів в гілках. Причому ці значення можуть бути значно більші струму на вході ланцюга. Тому такий резонанс отримав назву резонансу струмів.
Для схеми рис.7.2, в якій R2=0, при зміні індуктивності L або частоти ω мінімум повної провідності ланцюга, а також мінімум загального струму настає на інший частоті, відмінній від резонансної частоти ω0. Якщо ж перемінним параметром є ємність С, то провідність і загальний струм досягають мінімуму при резонансі струмів.
В радіотехніці широко застосовуються резонансні контури з малими втратами, для яких R1 і R2 малі порівняно з ρ і їх значеннями можна знехтувати. Тому далі розглядаються особливості контуру с паралельним з’єднанням R, L, C (рис.7.3). Провідність G=1/R може бути знайдена при малих R1, R2, з співвідношення: G=(R1+R2)/ρ2
i
|
|
iG |
|
|
|
iC |
|
|
iL |
|
|
|
|
|
|
|
|
|
|||
u |
G |
|
|
C |
|
|
|
L |
||
|
|
|
||||||||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис 7.3
Миттєві значення струмів в гілках ланцюга при значенні вхідної напруги u=Umsinωt: iG=GUmsin(ωt); iL=(1/L) ∫udt =(1/ωL)Umsin(ωt-π/2); iC=Cdu/dt=ωCUmsin(ωt+π/2);
Сумарний струм в ланцюзі: i= iG+ iL+ iC= GUmsin(ωt)-(1/ωL-ωC)Umsin(ωt-π/2)=Y Umsin(ωt-ϕ),
де: |Y|= G 2 +(1/ ωL −ωC) 2 - модуль вхідної провідності ланцюга;
ϕ=arctg (BL-BC)/G= arctg BВХ/G – зсув фаз між струмом і напругою на вході ланцюга; BL=1/ωL, BC=ωC; - провідності реактивних елементів;
BВХB = BL-BC – вхідна провідність ланцюга.
Якщо розглядати комплексну амплітуду сумарного струму, то її можна представити як векторну
|
− |
|
− |
− − |
суму комплексних амплітуд струмів: |
I |
= I G + I L − I C . |
||
Сумарна амплітуда струму ланцюга: |
I = |
IG2 |
+(I L −IC )2 |
|
Вираз для активної P, реактивної Q, повної потужності S, яку споживає ланцюг: P=0.5UmImcosϕ=0.5U2mG; Q=0.5UmIm sin ϕ=0.5U2mBBX; S=0.5UmIm=0.5U2m |Y|=  P 2 +Q 2 .
P 2 +Q 2 .
Умова передачі максимальної активної потужності в ланцюга визначається аналогічно тому, як це описано в ЛР-№6. Опір навантаження ZН (див. рис. 6.4) при резонансі ланцюга: ZН=LG/C.
Резонансна частота паралельного коливального контуру (см. рис. 7.3): ω0 |
= 1 |
|
LC |
28
Хвильова провідність γ чисельно дорівнює провідності реактивного елемента при резонансі:
γ=ω0С=1/ω0L=  C / L .
C / L .
Перевищення струмів в реактивних елементах над вхідним струмом ланцюга має місце при умові:
G<ω0С=1/ω0L=γ.
Величина, обернена добротності, називається затуханням контуру: α=1/Q=ImG/ImL= ImG/IC=Gω0L, де ImG, ImL, ImC – амплітудні значення струмів на елементах ланцюга при резонансі.
Залежність величин ( BL, BC, BBX, Y ) від частоти, називають частотними характеристиками ланцюга, а залежності значень струмів в гілках вхідного струму або відношень струмів від частоти –
резонансними характеристиками (кривими).
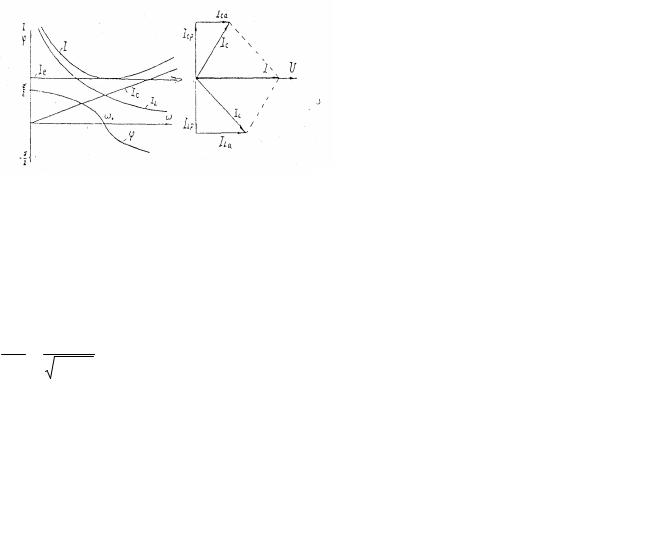
На рис. 7.4 побудовано частотні характеристики ідеального паралельного контуру, а на рис.7.5 представлено його резонансні характеристики (від джерела гармонічної напруги). На рис.7.5 наведено також векторні діаграми струмів в ланцюзі, де:
IR=U/R, IL=U/ωL, IC=UωC, I=UY (все для діючих амплітуд).
При застосуванні узагальненої розстройки ξ ( див. методичні вказівки до ЛР №6 ), вхідний опір паралельного контуру може бути представлено:
Z |
P |
= |
|
|
RP |
= |
|
|
RP |
−i |
RPξ |
|
; де R |
P |
= ρ2G - активний опір паралельного контуру при резонансі. |
|
1 |
+iξ |
1 |
+ξ2 |
1+ξ |
2 |
|||||||||||
|
|
|
|
|
|
|||||||||||
Вираз для нормованої резонансної кривої струму в реактивних елементах контуру:
Im |
= |
1 |
; де Im0 |
– амплітудне значення резонансного струму через реактивний елемент. |
||
Im0 |
1+ξ2 |
|||||
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 7.4. |
|
|
|
Рис.7.5 |
|
|
Таблиця 7.2 |
|
|
Варіанти завдань. |
|
|
|||
|
Варіант |
|
R L |
|
RC |
C нФ |
L мкГн |
RВН кОм |
|
|
|
Ом |
|
Ом |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0.2 |
|
0.1 |
1000 |
1000 |
1.5 |
|
2 |
|
0.8 |
|
0.2 |
100 |
500 |
3 |
|
3 |
|
0.6 |
|
0.2 |
500 |
1000 |
1 |
|
4 |
|
0.3 |
|
0.1 |
25 |
50 |
2 |
|
5 |
|
0.4 |
|
0.1 |
100 |
250 |
3 |
|
6 |
|
0.6 |
|
0.5 |
250 |
1000 |
2 |
|
7 |
|
0.4 |
|
0.1 |
100 |
200 |
2 |
|
8 |
|
0.2 |
|
0.1 |
300 |
500 |
4 |
|
9 |
|
1.4 |
|
0.05 |
30 |
300 |
3 |
|
10 |
|
0.4 |
|
0.1 |
150 |
400 |
3 |
29
Лабораторна робота № 8
Дослідження магнітного зв'язку і зв'язаних коливальних контурів
Стислий зміст роботи
В процесі виконання роботи досліджуються і вивчаються наступні питання:
1)Магнітний зв'язок між котушками, що входять в різні коливальні контури;
2)Явище резонансу в двох однакових зв’язаних коливальних контурах:
-повна настройка в резонанс зв’язаних коливальних контурів;
-вид резонансних кривих і перевірка аналітичних співвідношень.
Підготовка до роботи
1.При підготовці до роботи необхідно ознайомитися з методичними вказівками, робочим завданням, вивчити навчальну літературу, зробити всі розрахунки, зазначені цьому розділі та в робочому завданні та відповісти на наступні питання:
а) як враховується вплив магнітної зв’язку між двома котушками при складанні рівнянь ланцюгу за другим законом Кірхгофа?
б) характеризуйте зустрічне і взаємопогоджене вмикання двох послідовних котушок індуктивності і визначте теоретично їх сумарний опір в кожному з випадків; в) як експериментально визначити однойменні виводи двох магніто - зв’язаних котушок і величину їх взаємної індуктивності?
г) що собою представляє система двох зв’язаних коливальних контурів (характеризуйте коефіцієнт зв’язку і можливі типи і види зв’язку) ?
д) характеризуйте можливі види резонансних кривих коефіцієнта передачі по напрузі системи двох зв’язаних однакових контурів в залежності від параметра зв’язку; ж) перерахуєте види настройки системи двох зв’язаних контурів і дайте їх характеристику.
2.Скласти протокол звіту по лабораторній роботі.
Розрахувати ланцюг у відповідності з варіантом завдання: а) Для таблиць п.2 і п.4 з урахуванням п.5 робочого завдання;
б) Для таблиць п.8 з урахуванням п.7 робочого завдання у випадку простого часткового резонансу (першого для першого студента в підгрупі або другого для другого студента в підгрупі ). Теоретично довести цей випадок – простий частковий резонанс 2-х зв’язаних контурів і побудувати графічні залежності КU(jω)|, ϕU(ω);
в) Для таблиць п.9 робочого завдання в випадку повного резонансу. Теоретично довести цей випадок – повний резонанс 2-х зв’язаних контурів і побудувати графічні залежності КU(jω)|, ϕU(ω). Розрахувати критичний коефіцієнт зв’язку між зв'язаними контурами КсКР , по якому визначити значення критичного магнітного зв’язку МКР;
Робоче завдання
1. Зібрати схему для дослідження зв’язаних котушок індуктивності у відповідності з рис.8.1 і варіантом завдання (див. табл. 8.3). Значення номіналів опорів R1, R2 помножити на значення коефіцієнта К у відповідності з варіантом завдання.
I M
R1
L1 |
L2 |
R2 |
EГ
Рис.8.1 2.Встановити частоту генератора ЕГ у відповідності з варіантом завдання (див. табл. 8.3). Вихідну
напругу генератора встановити 10 В. В режимі часового моделювання ланцюга вимірювати струм в ланцюзі, напруги на елементах і зсув фаз між струмом в ланцюзі і напругою на її вході ϕ. Дані
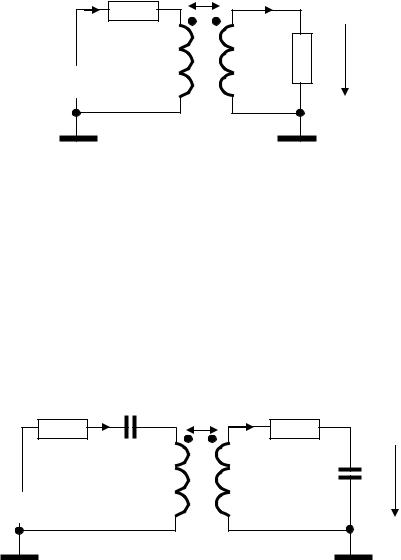
30
занести в табл. 8.1 |
|
|
|
|
|
|
|
табл. 8.1 ЕГ = |
fГ= |
|
|
|
|
|
|
|
I |
ϕ |
UR1 |
UL1 |
UR2 |
UL2 |
|
Експерим. |
|
|
|
|
|
|
|
Розрах. |
|
|
|
|
|
|
|
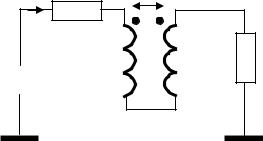
3.Зібрати схему для дослідження зв’язаних котушок індуктивності у відповідності з рис. 8.2 і
варіантом завдання (см. табл. 8.3). Значення номіналів опорів R1, R2 помножити на значення коефіцієнта К у відповідності з варіантом завдання.
4.Встановити частоту генератора ЕГ у відповідності з варіантом завдання (см. табл. 8.3). Вихідну напругу генератора встановити 10 В. В режимі часового моделювання ланцюга вимірювати струми
в ланцюзі, напруги на елементах. Вимірювати також зсув фаз ϕ1- між струмом в ланцюзі I1 і напругою на його вході (на генераторі), зсув фаз ϕU -- між напругою на виході ланцюга U2 і напругою на його вході U1 (на генераторі), коефіцієнт передачі по напрузі КU(jω) = U2 / EГ . Дані занести в табл. 8.2. В цьому випадку генератор-ідеальне джерело напруги.
I1 |
M I2 |
|
R1 |
|
|
L1 |
L2 |
R2 U2 |
EГ
|
|
|
|
Рис.8.2 |
|
|
|
|
|
|
табл.8.2 ЕГ = |
|
fГ= |
|
|
|
|
|
|
||
|
I1 |
UL1 |
|
UR1 |
ϕ1 |
I2 |
UR2 |
ϕU |
КU(jω) |
|
Експер. |
|
|
|
|
|
|
|
|
|
|
Розрах. |
|
|
|
|
|
|
|
|
|
|
5.Записати вихідні рівняння для схем на рис 8.1 і 8.2. Зробити розрахунок величин, наведених в табл. 8.1 і 8.2. Зробити висновки про дію магнітного зв’язку.
6.Зібрати схему для дослідження зв’язаних резонансних контурів у відповідності з рис. 8.3 і
варіантом завдання (см. табл. 8.3). Додаткові параметри схеми (значення М, С2 ) розрахувати у відповідності з п.7.
|
I1 |
M I2 |
|
R1 |
C1 |
|
R2 |
|
L1 |
L2 |
C2 U2 |
EГ
Рис.8.3
7. Вважаючи, що перший контур (L1, C1) настроєний на частоту настройки 2-х зв’язаних контурів – f0, обчислити необхідне значення ємності конденсатора C2 з формули власного резонансу другого контуру (L2, C2) на частоті f0. Обчислити також по відомим співвідношенням (див. ЛР.7)
