
amo_metoda
.pdf
|
|
n |
|
||||
|
|
2 max |
|
ij |
|
, |
(35) |
|
|
|
|||||
|
|
j i 1 |
|
|
|
|
|
третя канонічна норма – це корінь квадратний з сум квадратів модулів всіх елементів матриці коефіцієнтів :
|
|
3 |
|
|
ij |
|
2 . |
|
|
|
|||||
|
|
|
i j |
|
|
||
Наслідок 1: Ітераційний процес розв’язання системи (2.30) збігається, якщо сума модулів елементів рядків матриці коефіцієнтів або сума модулів елементів її стовпців менше за одиницю, тобто виконується умова
n |
n |
|
||||||||
max |
|
ij |
|
<1 або умова |
max |
|
ij |
|
<1. |
(36) |
|
|
|
|
|||||||
i j 1 |
|
|
|
|
j i 1 |
|
|
|
|
|
Наслідок 2: Ітераційний процес розв’язання системи (2.30) збігається, якщо елементи головної діагоналі більше суми модулів елементів відповідного рядка, крім діагонального елемента цього рядка, тобто виконується умова:
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
||||
|
|
|
ii |
|
|
max |
|
ij |
|
або умова |
|
jj |
|
max |
|
ij |
|
. |
(37) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
i |
|
j 1 |
|
|
|
|
|
|
|
|
|
|
j |
|
i 1 |
|
|
|
|
|
|
Приклад. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Визначити, чи збігається ітераційний процес для системи рівнянь |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 x3 |
20 |
|
|
|
3,25 0,125x2 |
0,125x3 |
|
||||||||||||||||||||
8x1 |
|
|
|
x1 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5x |
|
|
x |
|
7 |
|
або |
|
x |
|
1,4 0,2x |
|
0,2x |
|
|
|
|
|||||||||||
x |
1 |
2 |
3 |
|
|
2 |
1 |
3 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
x |
|
|
5x |
|
7 |
|
|
|
x |
|
1,4 0,2x |
|
0,2x |
|
|
|
|
|||||||||||
x |
1 |
2 |
|
3 |
|
|
|
3 |
1 |
2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Матриця |
|
даної системи має вигляд: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
0,125 |
0,125 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
0,2 |
|
0 |
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
0,2 |
|
0,2 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Визначаємо норми:

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
max |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
1 |
|
|
|
|
|
21 |
|
|
|
|
22 |
|
|
|
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
31 |
|
|
|
|
32 |
|
|
|
|
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
0 |
0,125 |
0,125 |
|
|
|
|
|
|
|
|
0,25 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,2 |
0 |
0,2 |
|
|
max |
|
0,4 |
|
0,4 |
1 |
||||||||||
max |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,2 |
0,2 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0,4 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
11 |
|
21 |
|
|
|
|
|
|
|
31 |
|
|
|
|
|
0 0,2 0,2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,125 0 0,2 |
|
|
||||
|
|
|
max |
|
|
|
|
|
|
|
|
|
|
|
|
|
max |
|
|||||||||||||
|
|
|
2 |
|
|
|
|
12 |
|
|
|
22 |
|
|
|
|
|
|
23 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,125 0,2 0 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
31 |
|
|
|
32 |
|
|
|
|
33 |
|
|
|
|
|
|
|
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
0,325 |
|
0,4 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
0,325 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким чином, перша та друга канонічні норми менші за одиницю, тобто ітераційний процес для даної системи збігається.
Розглянемо особливості алгоритмів наближених методів.
Метод послідовних наближень (метод Якобі)
Нехай задана система лінійних алгебраїчних рівнянь виду (28). Метод послідовних наближень (метод Якобі) відноситься до ітераційних методів, тому потребує перетворення даної системи до нормального вигляду (31) та пошуку канонічних норм матриці , для того, щоб визначити умови збіжності ітераційного процесу (34)–(36) пошуку розв’язку системи з заданою похибкоювідповідно до теореми про збіжність. Якщо жодна з умов (34) – (36) не виконується, то дану систему необхідно перетворити за певними правилами та знову перевірити умови збіжності ітераційного процесу (34) – (36). Якщо жодна з умов знову не виконується, то метод послідовних наближень не має сенсу використовувати. Якщо хоча б одна з умов (34)–(36) виконується, то ітераційний процес пошуку розв’язку системи з заданою похибкою збігається, і метод послідовних наближень можна використовувати.
По-перше, вибирається певне значення вектора початкових наближень x(0) , яке підставляється в праву частину системи рівнянь виду:

x |
(1) |
|
|
|
|
|
11 |
12 |
|
1 |
|
|
1 |
|
|||
|
(1) |
|
|
2 |
|
|
21 |
22 |
x |
2 |
|
|
|
|
|||
|
(1) |
|
|
3 |
|
|
311 |
32 |
x |
3 |
|
|
|
|
|||
|
|
|
|
... |
|
|
|
|
... |
|
|
|
....... ...... |
||||
|
|
|
|
|
|
|
n11 |
n2 |
x |
(1) |
|
|
|
|
|||
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
x1 |
(0) |
|
|
|
|
13 |
|
1n |
|
|
|
|
|
|
|
|
|
|
|
|
|
(0) |
|
|
|
23 |
... |
n2 |
x |
2 |
|
|
|
|
|
|
|
|
|
||||||
33 |
... |
|
|
|
(0) |
|
, |
(38) |
|
3n |
* x |
3 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
..... |
..... |
..... |
... |
|
|
|
|
||
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
n3 |
... |
nn |
x |
|
(0) |
|
|
|
|
|
n |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
що легко розв’язується для знаходження вектора розв’язку першого наближення x(1), тому що в правій частині містить всі визначені елементи. По-друге, перевіряється виконання умови закінчення ітераційного процесу виду: | x(1) x(0) | ,
де - задана похибка результатів розв’язання задачі. Якщо умова не виконується, то x(1) підставляється в праву частину системи (31) і знаходиться x(2):
x |
(2) |
|
|
|
|
|
11 |
12 |
13 |
|
1 |
|
|
1 |
|
||||
|
(2) |
|
|
2 |
|
|
21 |
22 |
23 |
x |
2 |
|
|
|
|
||||
|
(2) |
|
|
3 |
|
|
311 |
32 |
33 |
x |
3 |
|
|
|
|
||||
|
|
|
|
... |
|
|
|
|
|
... |
|
|
|
....... ...... ..... |
|||||
|
|
|
|
|
|
|
n11 |
n2 |
n3 |
x |
(2) |
|
|
|
|
||||
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
x1 |
(1) |
|
|
|
1n |
|
|
|
|
|
|
|
|
|
|
(1) |
|
... |
n2 |
x |
2 |
|
|
|
|
|
|||||
... |
|
|
|
(1) |
|
|
* x |
|
|||||
|
3n |
|
|
3 |
|
|
|
|
|
|
|
||
..... ..... |
... |
|
|
|||
|
|
|||||
|
|
|
|
|
|
|
... |
nn |
x |
|
(1) |
|
|
|
n |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
та знову перевіряється виконання умови закінчення ітераційного процесу
виду: | |
|
(2) |
|
(1) |
| . |
|
|
|
|
|
x |
x |
|
|
|
|
|
||||
За аналогією |
будь-яке |
k 1 -e |
наближення |
можна обчислити за |
||||||
формулою: |
|
|
|
|
|
|
||||
|
|
|
|
|
_ |
_ |
_ |
_ |
|
|
|
|
|
|
|
x(k 1) |
* x(k) , |
де k 1,2,... |
(39) |
||
Якщо послідовність x(0),x(1),x(2),...,x(k), отримана в результаті |
||||||||||
ітераційного процесу, має границю |
x lim xk , то ця границя є розв’язком |
|||||||||
|
|
|
|
|
|
|
|
|
k |
|
системи. Умова закінчення ітераційного процесу має вигляд:
_ |
|
| x(k 1) x(k) | , |
(40) |
де - задана похибка результатів розв’язання системи.
Алгоритмічно перевірка умови (40) представляє собою алгоритм пошуку
максимального відхилення між координатами вектора x(k) і x(k 1) і порівняння його з заданою похибкою .
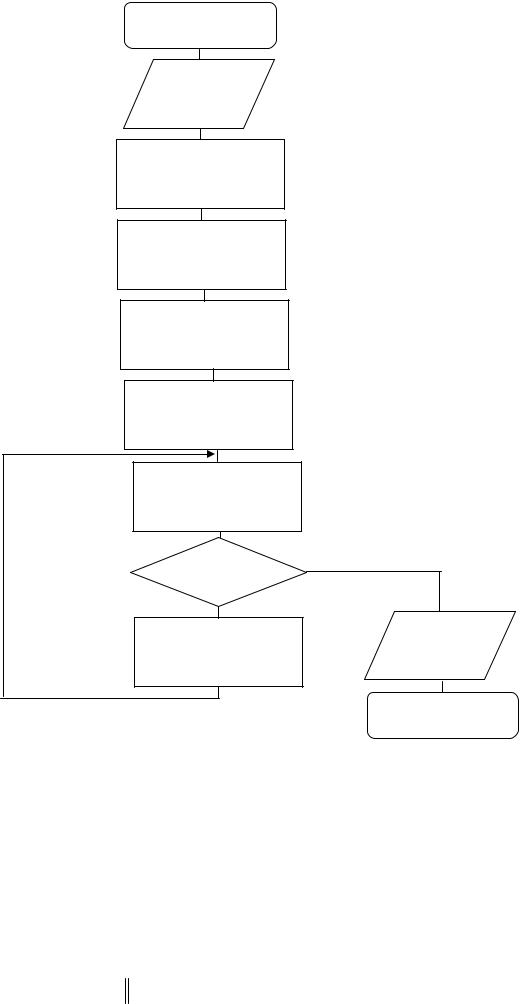
Алгоритм методу послідовних наближень зображено на рис. 5
Початок
Ввід
вхідних
даних
Зведення СЛАР до
нормального вигляду
Перевірка умови
|| ||i<1
Визначення
теоретичного числа ітерацій кТ
Вибір вектору
початкових значень X0
Обчислювання
x(k+1)= + *x(k)
|xk+1-xk|< 1
0
заміна
x(k+1)=x(k)
Вивід
X,K,кТ
Кінець
Рис. 5. Схема алгоритму методу послідовних наближень
Оцінка похибки методу Якобі |
|
|
Якщо задана допустима похибка обчислень |
і x – вектор |
точного |
розв’язку системи лінійних рівнянь, а x(jk) k -те |
наближення до |
вектору |
точного розв’язку, то для оцінки похибки метода послідовних наближень використовується формула:
xj xkj |
|
|
|
|
|
|
|
|
|
|
|
|
|
(k 1) |
, |
(41) |
||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

де |
|
|
|
|
|
|
|
- одна з 3 норм матриці ; |
|
|
|
|
|
|
|
- аналогічна норма вектора ; |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k - кількість ітерацій, необхідна для досягнення потрібної точності .
Метод Гауса-Зейделя
Метод Зейделя є модифікацію методу послідовних наближень, причому у методі Зейделя при обчисленні i -ої координати вектора розв’язку (k 1)-го
наближення використовуються значення всіх i 1 координат вектора (k 1)-е наближення, обчислені раніше. Розглянемо метод більш детально.
Нехай початкова система лінійних алгебраїчних рівнянь приведена до нормального вигляду:
|
|
x |
x |
|
x |
; |
|
||||
x |
1 |
|
|||||||||
|
1 |
11 1 |
|
12 2 |
|
|
1n n |
|
|
|
|
|
|
x |
|
x |
|
|
x |
|
; |
|
|
x |
2 |
|
|
|
|
||||||
|
2 |
21 1 |
|
22 2 |
|
|
2n n |
|
(42) |
||
|
|
|
|
|
|
|
|
|
|
|
|
........................................................ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
x |
|
|
x |
|
. |
||
x |
n |
|
|
|
|||||||
|
n |
n1 1 |
n2 2 |
|
nn n |
|
|||||
Алгоритм Гауса-Зейделя
1.Вибрати значення координат вектора початкових наближень
xx1(0),...,xn(0)
2.Визначити значення першої координатиx1(1) вектора першого наближення
зпершого рівняння системи:
x1(1) 1 11x1(0) 12x2(0) ... 1nxn(0).
3.Підставити в друге рівняння системи значення першої координатиx1(1), яке обчислено на попередньому кроці
x2(1) 1 21x1(1) 22x2(0) ... 2nxn(0).
4.Отримані значення координат першого наближення x1(1), x2(1) підставляємо
утретє рівняння системи (39)
x3(1) 1 21x1(1) 22x2(1) 23x3(0) ... 2nxn(0)
для знаходження третьої координати і т. д.
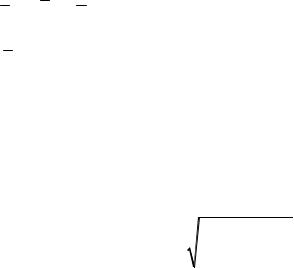
5.Для знаходження останньої координати вектора першого наближення xn(1)в останнє рівняння системи треба підставити значення всіх n 1
координат (x1(1),x2(1),x3,(1) ,xn(1)1), які отримані на попередніх кроках, та значення координати xn(0)
xn(1) n n1x1(1) n2x2(1) ... n,n 1xn(1)1 nnxn(0).
6.Аналогічно будують друге, третє та інші наближення. Так, для вектора
k 1 -го наближення за методом Зейделя використовують наступні формули:
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(k 1) |
|
|
|
|
(k) |
|
|
|
|
|
|
|
|
||
|
|
|
x |
|
|
|
|
|
|
|
|
|||||
x |
1 |
j |
; |
|
|
|
|
|
|
|
|
|||||
|
1 |
1j |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(k 1) |
|
|
|
|
(k) |
|
|
(k 1) |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
2 2jxj |
|
21xj |
|
; |
|
|
|
|||||||
x |
|
|
|
|
|
|||||||||||
|
|
|
j 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
(k 1) |
|
(k 1) |
|
|
|
(k 1) |
(k) |
|
|
||||||
|
|
32x |
|
; |
(43) |
|||||||||||
x |
3 |
3 31x1 |
|
|
|
|
2 |
|
3jxj |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
j 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
....................................................................... |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(k 1) |
|
|
|
x |
(k 1) |
x |
(k) |
|
|
|
|||||
x |
n |
|
j |
|
|
n |
. |
|
|
|
||||||
|
n |
nj |
|
|
|
|
|
nn |
|
|
|
|
||||
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Умови збіжності ітераційного процесу Зейделя
Даний процес розв’язання СЛАР – ітераційний, тому важливим є аналіз умов збіжності ітераційного процесу. Процес Зейделя для системи лінійних
рівнянь x x збігається до точного розв’язку з заданою похибкою при
будь-якому виборі вектора початкових наближень, якщо будь-яка норма матриці менша 1, тобто якщо:
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
1 |
max |
|
|
|
ij |
|
|
|
|
|
1 |
(44) |
||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
max |
|
|
|
ij |
|
|
|
|
|
1 |
(45) |
||||||
|
|
|
2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
3 |
|
|
|
ij |
|
|
|
|
|
2 1 |
(46) |
||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
i |
j |
|
|
|
|
|
|
|
|
||||||
Відомо, що процес |
Зейделя |
сходиться до точного |
розв’язку СЛАР |
|||||||||||||||||||
швидше, ніж метод послідовних наближень.
Приклад. Знайти першу та другу норми та проаналізувати умови збіжності ітераційного процесу для матриці α, яка має вигляд :
|
|
|
0,24 |
-0,05 |
-0,24 |
|
|
|
|
|
|||
|
|
|
022 |
0,09 |
-0,44 |
|
|
|
|||||
|
|
|||||
|
|
|
0,13 |
-0,02 |
0,42 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
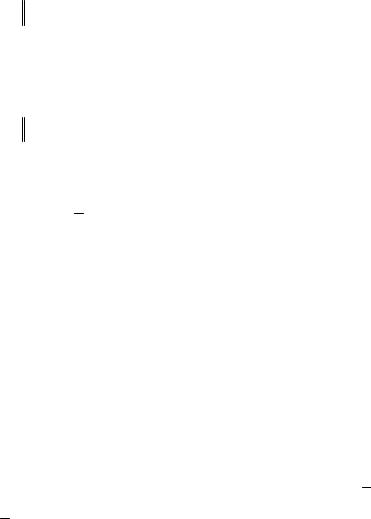
|
|
|
n |
|
|
||
|
|
1 maxj |
|
|
ij |
|
max 0,53; 0,75; 0,57 0,75 1. |
|
|
|
|||||
|
|
|
j 1 |
|
|
|
|
Очевидно, що процес ітерації для даної системи сходиться до точного розв’язку, незважаючи на те, що
|
|
|
|
n |
|
|
||
|
|
|
max |
|
ij |
|
max{0,59; 0,16; 1,1}=1,1>1. |
|
|
2 |
|
|
|||||
|
|
|
i |
|
|
|
|
|
|
|
|
j 1 |
|
|
|||
|
|
|
|
|
|
|||
Оцінка похибки методу Гауса-Зейделя
Якщо x – точне значення вектора розв’язку системи лінійних рівнянь; а
|
|
(k)- к-е наближення, обчислене за методом |
|
Гауса-Зейделя, то для оцінки |
|||||||||||||||||||||||||||||||||
x |
|||||||||||||||||||||||||||||||||||||
похибки цього методу використовується формула: |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
(k) |
|
|
|
|
|
|
|
|
|
|
|
|
|
(k) |
|
|
|
|
|
(1) |
|
|
(0) |
|
(47) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
x |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Метод верхньої релаксації
В основі методу верхньої релаксації використовується алгоритм та обчислювальна схема метода Гауса-Зейделя, але на відміну від нього нові значення координат вектора k -го наближення визначаються за формулами:
xi(k 1) xi(k) ( |
xi(k 1) xi(k)), |
(48) |
де |
xi(k 1)- уточнене |
значення змінної по |
методу Гауса-Зейделя, - параметр |
релаксації, значення |
якого визначається |
з інтервалу 1 2. При =1 |
|
метод тотожний методу Гауса-Зейделя. Швидкість збіжності ітераційного процесу залежить від значення .
Контрольні запитання
1.Дати визначення термінів: розв’язання СЛАР, визначена і невизначена, вироджена, сумісна і несумісна СЛАР.
2.Класифікація методів розв’язання СЛАР.
3.Суть точних методів розв’язання СЛАР.
4.У яких випадках краще використовувати точні методи?
5.Суть алгоритму методу Гауса розв’язання СЛАР.
6.У чому різниця між алгоритмами методів Гауса з послідовним виключенням невідомих і з вибиранням головного елементу; що спільного?
7.У чому суть методу Гауса за схемою Халецького?
8.Порівняйте алгоритми методів Гауса з вибиранням головного елементу і за схемою Халецького. Обчислення за яким з цих алгоритмів швидше? Який із алгоритмів ефективніший?
9.В чому суть методу Гауса за схемою Халецького?
10.Яку систему отримано в результаті прямого ходу методу Гауса-Жордана?

11. Дати визначення термінів: розв’язання СЛАР, норма матриці, норма вектора, достатня умова збіжності.
12. Привести СЛАР: 9,9х1 -1,5х2+2,6х3=0; 0,4х1+13,6х2-4,2х3=8,2; 0,7х1+0,4х2+7,1х3=-13;
до нормального вигляду.
Порядок виконання роботи
1.Ознайомитись з відомими точними чисельними методами розв'язання систем лінійних алгебраїчних рівнянь (СЛАР).
2.Скласти схему алгоритму розв’язання систем лінійних алгебраїчних рівнянь методом, вказаним викладачем.
3.Скласти програму розв'язання систем лінійних алгебраїчних рівнянь на алгоритмічній мові Pascal.
4.Користуючись даними відповідного варіанту (табл.1), розв’язати СЛАР на ЕОМ (початкові дані та результати роздрукувати).
5.Оформити звіт.
Звіт по лабораторній роботі повинен містити:
1)файл вихідного тексту програми;
2)файли результатів для тестового прикладу і для інтерполяції заданої функції;
3)опис алгоритму розрахунку (в текстовій формі та у вигляді блок-схеми) в електронному та роздрукованому вигляді;
4)роздруківку файлів з коментарями;
5)загальні висновки за результатами роботи, що включають результати тестування, отримані оцінки похибки результатів і обґрунтування цих оцінок.
Варіанти лабораторної роботи приведені в таблиці 1.
|
|
|
|
|
|
|
Таблиця 1 – Варіанти завдань |
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
Номер |
Матриця коефіцієнтів |
Стовпець |
|
Примітка |
|
|
|||||
|
|
|
|
|
||||||||
|
варіанту |
|
системи |
|
вільних членів |
|
|
|||||
|
|
1 |
1 |
2 |
-1 |
|
x1 1 |
|
||||
|
1 |
2 |
1 2 |
-4 |
|
x2 2 |
|
|||||
|
|
|
4 |
1 |
4 |
|
2 |
|
x3 2 |
|
|
|
|
|
1 |
3 |
2 |
1 |
|
x1 2 |
|
||||
|
2 |
3 |
4 |
0 |
2 |
|
x2 |
1 |
|
|||
|
|
|
2 |
5 |
3 |
|
2 |
|
x3 |
1 |
|
|
|
|
1 |
3 |
2 |
5 |
|
x1 5 |
|
||||
|
3 |
3 |
4 |
0 |
7 |
|
x2 |
2 |
|
|||
|
|
|
2 |
5 |
3 |
|
9 |
|
x3 |
3 |
|
|

4
5
6
7
8
9
10
11
12
1 |
1 |
1 |
2 |
3 |
1 |
1 |
1 |
1 |
|
|
|
1 |
3 |
2 |
3 |
4 |
0 |
2 |
5 |
3 |
|
|
|
0,63 1,00 0,71 0,34
1,17 0,18 0,65 0,71
2,71 0,75 1,17 2,35
3,58 0,21 3,45 1,18
7,09 1,17 2,23
0,43 1,40 0,62
3,21 4,25 2,13
1,84 2,25 2,58
2,32 2,00 2,82
1,83 2,06 2,24
2,36 2,37 2,13
2,51 2,40 2,10
2,59 2,41 2,06
6,1 |
0,7 |
0,05 |
|||
1,3 2,05 |
|
0,87 |
|||
2,5 |
3,12 |
5,03 |
|||
|
|
|
|
|
|
8,7 |
3,1 |
1,8 |
|
2,2 |
|
2,1 |
|
6,7 |
2,2 |
0 |
|
3,2 |
1,8 |
9,5 |
1,9 |
||
1,2 |
|
2,8 |
1,4 |
9,9 |
|
|
|
|
|
|
|
2,58 2,98 3,13
1,32 1,55 1,58
2,09 2,25 2,84
4 |
|
x1 1 |
|
9 |
|
x2 |
2 |
-2 |
|
x3 |
1 |
|
|
||
-5 |
|
x1 6 |
|
-2 |
|
x2 |
5 |
-7 |
|
x3 |
2 |
|
|
||
2,08 |
x1 0.4026 |
||
0,17 |
x2 |
1.5016 |
|
1,28 |
x3 |
0.5862 |
|
0,05 |
x4 0.2678 |
||
|
|||
-4,75 |
x1 0.2386 |
||
-1,05 |
x2 |
0.5945 |
|
-5,06 |
x3 |
3.2019 |
|
|
|||
-6,09 |
|
|
|
-6,96 |
|
|
|
-5,52 |
|
|
|
|
|
|
|
1,48 |
|
|
|
1,92 |
|
|
|
2,16 |
|
|
|
|
|
||
6,97 |
x1 1.22 |
||
0,10 |
x2 |
0.67 |
|
2,04 |
x3 |
0.35 |
|
|
|||
-9,7 |
x1 0.72 |
||
13,1 |
x2 |
1.88 |
|
6,9 |
x3 |
0.92 |
|
25,1 |
x4 |
1.94 |
|
|
|||
-6,66 |
|
|
|
-3,58 |
|
|
|
-5,01 |
|
|
|
|
|
|
|
13
14
15
16
17
18
19
20
21
1,54 1,70 1,62
3,69 3,73 3,59
2,45 2,43 2,25
7,6 |
0,5 |
2,4 |
2,2 |
9,1 |
4,4 |
1,3 |
0,2 |
5,8 |
8 |
1 |
1 |
1 |
5 |
1 |
1 |
1 |
5 |
|
|
|
2 |
1 |
4 |
2 |
1 |
3 |
3 |
4 |
5 |
|
|
|
11 |
3 |
1 |
2 |
5 |
5 |
1 |
1 |
1 |
1 |
4 |
0 |
1 |
1 |
1 |
2 |
3 |
2 |
3 |
1 |
1 |
1 |
2 |
3 |
1 |
|
|
|
|
2 |
0 |
1 |
2 |
0 |
1 |
2 |
1 |
1 |
1 |
0 |
1 |
1 |
3 |
2 |
0 |
|
|
|
|
1,14 2,15 5,11
0,42 1,13 7,050,71 0,81 0,02
0,61 0,71 0,051,03 2,05 0,87 2,5 3,12 5,03
-1,97 -3,69 -5,98
1,9 |
x1 0.248 |
||
9,7 |
x2 |
1.114 |
|
-1,4 |
x3 0.224 |
||
|
|||
26 |
|
x1 3 |
|
7 |
|
x2 |
1 |
7 |
|
x3 |
1 |
|
|
||
7 |
|
x1 0 |
|
-5 |
|
x2 |
1 |
-14 |
|
x3 |
2 |
|
|
||
15 |
|
x1 2 |
|
-11 |
|
x2 |
2 |
1 |
|
x3 |
1 |
|
|
||
6 |
|
x1 1 |
|
-1 |
|
x2 1 |
|
-1 |
|
x3 |
1 |
3 |
|
x4 1 |
|
|
|
||
-8 |
|
x1 1 |
|
-1 |
|
x2 |
2 |
-6 |
|
x3 |
0 |
7 |
|
x4 |
3 |
|
|
||
2,05 |
x1 1.12 |
||
0,80 |
x2 |
0.341 |
|
-1,07 |
x3 0.008 |
||
|
|||
-0,16 |
x1 0.008 |
||
0,50 |
x2 |
0.231 |
|
0,95 |
x3 |
0.042 |
|
|
|||
