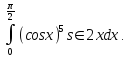Підготовка до КРЗЗ-2 за 1-й курс
.docxЗадачі для підготовки до КР з вищої математики за І курс
(КРЗЗ-2 проводиться на 1-му практичному занятті в вересні)
Всього в КР 7 задач такого типу
Задача 1.
-
Знайти кут B трикутника АВС, якщо А(-1,-2,4), В(-4,-2,0), С(3,-2,1). Відповідь: В =
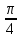 ( через скалярний добуток).
( через скалярний добуток). -
Обчислити площу трикутника АВС, А(1,1,1), В(2,3,4), С(4,3,2). Відповідь: S =2
 (Sтр
=
(Sтр
=
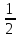 |[
|[
 ,
,
 ]|
(векторний добуток).
]|
(векторний добуток). -
Знайти об’єм піраміди ABCD, якщо її вершини А(2,-3,5), В(0,2,1), С(-2,-2,3), D (3,2,4). Відповідь: V = 6. (Vпір = =
 │
│ ,
,
 ,
,
 │-
модуль мішаного добутку).
│-
модуль мішаного добутку). -
Знайти розклад вектора
 = (-10, 4) за базисом
= (-10, 4) за базисом
 = (1, -2),
= (1, -2),
 = (-3, 2).
= (-3, 2).
Відповідь:
 =2
=2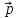 +4
+4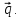
-
Знайти відстань від точки М(-1, 2) до прямої L: -2x+y-1=0. Відповідь: d =
 .
( d
=
.
( d
=
 ).
). -
Знайти відстань від початку координат до прямої, яка проходить через точки (5,2) та (-3,-2). Відповідь:
 .
. -
Скласти рівняння прямої, яка проходить через точку М(-1,2), перпендикулярно до прямої L: -2x+y-1=0. Відповідь: у =−
 .
. -
Знайти проекцію точки М(-1,2) на пряму L: -2x+y-1=0. Відповідь: (
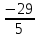 ,
,
 ).
).
-
Знайти точку В, симетричну точці А(1,2) відносно прямої L: 3x-y+9 = 0. Відповідь: В(-5,4).
-
Знайти відстань від центра кола x2 + y2 -4x + 6y -3 = 0 до початку координат. Відповідь:
 .
. -
Написати рівняння кола, якщо точки М1(5,-1) та М2(1,2) є кінцями одного з його діаметрів. Відповідь: (х-3)2+(у-
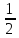 )2
=
)2
=
 .
. -
Написати рівняння дотичної до еліпса x2 + 4y2 = 40 в точці (2,-3). Відповідь: у+3 =
 (х-2).
(х-2).
Задача 2. Обчислити визначений інтеграл.
-
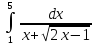 ,
Зробити заміну змінної t
=
,
Зробити заміну змінної t
=
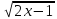 .
.
-
 ,
Зробити заміну змінної t
=
,
Зробити заміну змінної t
=
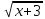 .
.
-
 ,
Зробити заміну змінної x
= sint.
,
Зробити заміну змінної x
= sint.
-
 ,
Зробити заміну змінної
x
=
,
Зробити заміну змінної
x
=
 .
.
-
 ,
Зробити заміну змінної
x+1=
2sint.
,
Зробити заміну змінної
x+1=
2sint.
-
 ,
Зробити
заміну змінної t
= tg
,
Зробити
заміну змінної t
= tg .
.
Задача 3. Обчислити невизначений інтеграл типу
 , де D<0
, де D<0
Наприклад:
 .
Відповідь:
.
Відповідь:
 ln|3x2+2x+1|
-
ln|3x2+2x+1|
-
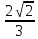 arctg
arctg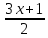 +C.
+C.
Задача 4.
-
Написати формулу Маклорена 3-го порядку з залишковим членом в формі Лагранжа для функції f(x) = chx (або f(x) = cos2x, … ).
-
Написати формулу Тейлора 2-го порядку в околі точки х0=1 для функції f(x) =
 .
Залишковий
член в формі Лагранжа.
.
Залишковий
член в формі Лагранжа.
Задача 5. Знайти екстремуми функцій однієї або двох змінних.
-
f(x) = x3e-x ; f(x) = x2 +
 ; f(x) = x-2lnx.
; f(x) = x-2lnx. -
z = x2+y2-2x+4y+10; z = (x-5)2+y2+1 (TР-2. Зад 4.)
Задача 6. Знайти загальний розв’язок ЛНДР 2-го порядку зі сталими коефіцієнтами та правою частиною спеціального вигляду, або методом Лагранжа.
-
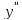 +9y
= -6sin3x;
2)
+9y
= -6sin3x;
2)
 +2
+2 +y
=
+y
=
 (ТР-2. Зад. 31, 32).
(ТР-2. Зад. 31, 32).
Задача 7. Розв’язати систему ДР.
-
 (ТР-2.
Зад.33).
(ТР-2.
Зад.33).