2. Динамічне рівняння руху матеріальної точки у координатній та натуральній формі ( формі Ейлера). Зміст першої задачі динаміки точки.
Динамічні (диференціальні) рівняння руху МТ – встановлює математичну залежність між кінематич характер руху точки та силами
Перша (пряма) задача динаміки точки: визначення невідомої сили за відомою масою та кінематичним законом руху.
3. Зміст другої задачі динаміки точки. Інтеграли рівнянь руху точки. Початкові умови.
Друга задача динаміки – обернена задача, задача інтегрування.
Нехай є сили, маса, потрібно знайти x(t), y(t), z(t).
перший інтеграл,
Припустимо що 1.1 =>
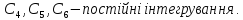
Припустимо що з 1.3 випливає:
Сталі інтегрування визначимо за допомогою початкових умов.
Початкові
умови – значення координат точки та
проекції швидкості у
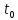(коорд.
спосіб).
При натуральному способі – значення дугової координати та швидкості.
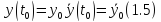
Визначення сталих інтегрування – задача Коші.
Для їх визначення треба підставити у 1.4 похідні цих виразів.
Отримаємо 6 рівнянь та 6 невідомих.
4. Класифікація в’язей. Рівняння Лагранжа першого роду.
В’язь називається стаціонарною якщо у її р-ня не входить час f(x,y,z). Нестаціонарна f(x,y,z,t). Геометрична в’язь – у її р-ня входять координати точки f(x,y,z) чи f(x,y,z,t).Утримувальна в’язь (двостороння) – в’язь при накладанні якої до кожного переміщення точки існує протилеж.
Жорсткий стержень = l
;
Утримувальна в’язь (одностороння) – в’язь при накладанні якої не до кожного переміщення точки існує протилежність. (малюнок такий самий тільки замість стержня нитка)
;
Кінематична в’язь – у р-ня якої входять швидкість точки і можливо час. Усі геометричні та інтегровані кінематичні в’язі називаються голономні в‘язі. Неголономні- в’язі не інтегровані кінематичні. Ідеальна в’язь – в’язь напрям реакції якої визнач наперед виходячи з її фізич вл. До ідеальних в’язей відносяться: 1)точкові ідеальні шарніри 2)ідеальні стержні 3) ідеально гладкі поверхні 4)котки
Р-ня Лагранжа І-го роду:
Припустимо,
що рух т.М обмеж ідеальною в’яззю. В’язь
реалізується у вигляді поверхні.
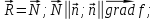
f(x,y,z)=0 рівняння поверх (в’язі)
;
;
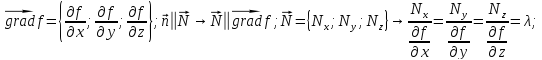-Рівняння
Лагранжа І-го роду.
-
множник Лагранжа.
5. Принцип д’Аламбера для матеріальної точки. Сила інерції та її фізичний зміст. Способи визначення.
6.
Принцип Д’Аламбера
для системи матеріальних точок.
7. Визначення головного вектора та головного момента системи сил інерції в загальному випадку та при поступальному русі системи точок.
8. Визначення головного вектора та головного момента системи сил інерції при обертальному русі системи точок.
9. Динамічне рівняння відносного руху матеріальної точки. Ейлерові сили інерції. Умова відносного спокою. Принцип відносності Галілея.
10. Виведення диференціального рівняння вільних коливань точки без урахування сил опору та його розв'язок. Визначення сталих інтегрування. Амплітуда, частота та період коливань.
________________________________________________________
13. Розв’язок диференціального рівняння вільних коливань з урахуванням сил опору у випадку малого опору. Визначення сталих інтегрування. Залежність між амплітудами коливань. Декремент коливань.
14. Виведення диференціального рівняння змушених коливань без урахування сили опору. Визначення частинного розв’язку у нерезонансному випадку та його коефіцієнтів.
15. Виведення диференціального рівняння змушених коливань без урахування сили опору. Визначення частинного розв’язку у резонансному випадку та його коефіцієнтів. Зсув фази змушених коливань.
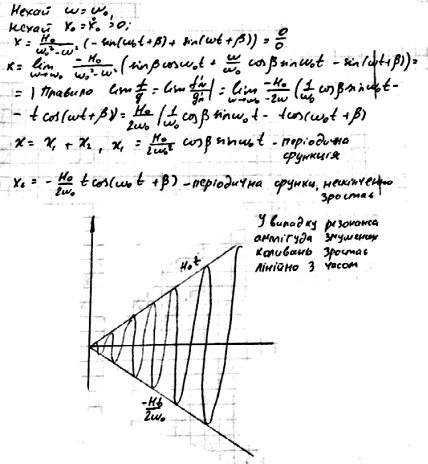
16. Виведення диференціального рівняння змушених коливань з урахуванням сили опору. Визначення загальної форми частинного розв’язку та його коефіцієнтів.
17. Визначити залежність коефіцієнта динамічності змушених коливань з урахуванням сили опору від частоти збурювальної сили. Амплітудно-частотна характеристика. Фазо-частотна характеристика.
