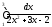Додаток 2
Приклад програми, яка обчислює суму перших при перегляді масиву додатного та від’ємного елементів масиву.
#include <iostream.h>
#include <conio.h>
const int n=4,l=3;
struct result // структура з результатами
{
int suma,ind1,ind2; //сума та індекси елементів масиву
};
//variant 1: функція повертає суму елементів
int fun1(int arr[],int m)
{
int sum=0;
for(int i=0;i<m;i++)
if(arr[i]>0)
{
sum+=arr[i];break;
}
for(i=0;i<m;i++)
if(arr[i]<0)
{
sum+=arr[i];break;
}
return sum;
}
//variant 2: функція повертає усі потрібні результати (суму та //індекси елементів) через список /формальних аргументів;
void fun2(int arr[],int m,int *sum,int *index1,int *index2)
{
*sum=0;
for(int i=0;i<m;i++)
if(arr[i]>0)
{
*sum+=arr[i];*index1=i;break;
}
for(i=0;i<m;i++)
if(arr[i]<0)
{
*sum+=arr[i];*index2=i;break;
}
}
//variant 3: функція повертає структуру із усіма потрібними результатами
result fun3(int arr[],int m)
{
result a={0,0,0};
for(int i=0;i<m;i++)
if(arr[i]>0)
{
a.suma+=arr[i];a.ind1=i;break;
}
for(i=0;i<m;i++)
if(arr[i]<0)
{
a.suma+=arr[i];a.ind2=i;break;
}
return a;
}
//variant 4: функція повертає вказівник на масив із усіма потрібними
// результатами
int *fun4(int arr[],int m)
{
int *g=new int[l];g[0]=0;
for(int i=0;i<m;i++)
if(arr[i]>0)
{
g[0]+=arr[i];g[1]=i;break;
}
for(i=0;i<m;i++)
if(arr[i]<0)
{
g[0]+=arr[i];g[2]=i;break;
}
return g;
}
//variant 5: функція отримує масив в для заповнення усіма //потрібними результатами через список формальних аргументів.
void fun5(int arr[],int m,int b[])
{
b[0]=0;
for(int i=0;i<m;i++)
if(arr[i]>0)
{
b[0]+=arr[i];b[1]=i;break;
}
for(i=0;i<m;i++)
if(arr[i]<0)
{
b[0]+=arr[i];b[2]=i;break;
}
}
void main()
{
int mas[n]={0,-3,-5,13},sum,index1,index2,*res,res1[l];
//input(mas); output(mas);
res=new int[l]; //динамічний масив результатів
clrscr();
//variant 1 call
sum=fun1(mas,n);
cout<<"\n sum="<<sum;
//variant 2 call
fun2(mas,n,&sum,&index1,&index2);
cout<<"\n sum="<<sum<<" index1="<<index1<<" index2="<<index2;
//variant 3 call
result q=fun3(mas,n);
cout<<"\n sum="<<q.suma<<" index1="<<q.ind1<<" index2="<<q.ind2;
//variant 4 call
res=fun4(mas,n);
cout<<"\n sum="<<res[0]<<" index1="<<res[1]<<" index2="<<res[2];
//variant 5 call
fun5(mas,n,res1);
cout<<"\n sum="<<res1[0]<<" index1="<<res1[1]<<" index2="<<res1[2];
getch();
}
Результати виконання тесту
sum=10
sum=10 index1=3 index2=1
sum=10 index1=3 index2=1
sum=10 index1=3 index2=1
sum=10 index1=3 index2=1
Лабораторна робота № 6
ОБЧИСЛЕННЯ ВИЗНАЧЕНОГО ІНТЕГРАЛУ
Мета роботи – вивчення методу чисельного інтегрування ,складання програми чисельного обчислення визначеного інтегралу , дослідження точності розрахунків.
Порядок виконання роботи
А.При пiдготовцi :
1. Ознайомитися з методом чисельного обчислення визначеного інтегралу ( Крилов В.И. Приближенное вычисление определенных интегралов.-М.Наука,1967 та додаток А ).
2.Розробити алгоритм програми обрахунку визначеного інтеграла (таблиця )
3.Скласти програму обчислення інтеграла, підінтегральну функцію записати окремою функцією в програмі. Передбачити у програмі обчислення інтегралу з заданою точністю к ≤ 10-6 … 10-5 та з різними кроками для дослідження залежності значення інтегралу від кроку (кількості проміжків n ) з метою визначення оптимального n .
4.Підготувати проект звіту.
В.У лабораторii:
1. Ввести в ПК підготовлену програму .Для налагодження програми використати стандартний інтеграл
= 2 .
2. Обчислити інтеграл з заданою точністю к ≤ 10-6 … 10-5 .
3. Визначити оптимальний n (побудувати у звіті залежність значення інтегралу від кількості проміжків n ).
Змiст звiту:
1.Блок-схема алгоритму або граф обчислювального процесу (Д.Мак-Кракен,У.Дорн Численные методы и программирование на Фортране.-М.;Мир,1977 ).
2.Програма з коментарем.
3. Результати виконання обчислень.
4. Висновки по роботi.
Додаток А
Алгоритми обчислення визначеного інтегралу зводяться до обчислення площі криволінійної трапеції шляхом її розбиття на елементарні фігури, площі яких можна легко обчислити, та обчислення суми площ цих елементарних фігур (з урахуванням знаку). Для зручності крок розбиття обирають сталою величиною для всіх елементарних фігур. На рисунку зображений приклад розбиття криволінійної трапеції на елементарні фігури
n
– кількість проміжків розбиття,
- крок.
Формула Сімпсона за методом парабол працює для парної кількості проміжків n
I
=
,
Похибка
обмеження методу дорівнює
e = - h4 *(b-a) * fiV (ξ)/180 , a < ξ < b .
Верхня
границя можливої похибки округлення
пропорційна 1/h
.Таким
чином, зі зменшенням кроку h
зменшується
похибка обмеження методу ,але збільшується
похибка округлення обчислень.
Наприклад
,для
загальна
помилка зростає для n
> 50 . Оцінити
похибку обмеження методу можна , виконуючи
розрахунки з різним кроком
I = I1 + c* h14 , I =I2 + c* h24 , c = (I2 – I1)/( h14 - h24) ,
I = I1 + h14 * (I2 – I1)/( h14 - h24) = I1 + (I2 - I1)/ (1 - h24 /h14 ) .
Екстраполяційний перехід Річардсона для h1 = h , h2 = h/2 має такий вигляд I = I1 + (I2 – I1) *16/15 .
Похибка R для кроку h1 становить за методом Рунге R=16(I2 – I1)/15.
Обчислення інтегралу із заданою точністю передбачає виконання наступної умови : R <= k , де k – допустима похибка ,наприклад , k = 10-6 .
Таблиця інтегралів
|
Варіант |
Інтеграл |
Кількість проміжків |
Варіант |
Інтеграл |
Кількість проміжків |
|
1 |
|
10 |
2 |
|
10 |
|
3 |
|
20 |
4 |
|
30 |
|
5 |
|
10 |
6 |
|
10 |
|
7 |
|
20 |
8 |
|
20 |
|
9 |
|
20 |
10 |
|
16 |
|
11 |
|
30 |
12 |
|
20 |
|
13 |
|
10 |
14 |
|
10 |
|
15 |
|
20 |
16 |
|
30 |
|
17 |
|
10 |
18 |
|
20 |
|
19 |
|
16 |
20 |
|
10 |
|
21 |
|
20 |
22 |
|
30 |
|
23 |
|
10 |
24 |
|
16 |
|
25 |
|
30 |
26 |
|
20 |
|
27 |
|
10 |
28 |
|
30 |
|
29 |
|
20 |
30 |
|
20 |
Розрахунок чисельного значення визначеного інтегралу у Mathcad
Вибрати у табло Calculus визначений інтеграл і вставити діапазон інтегрування та підінтегральну функцію , ввести „ = „ і отримати результат.
Лабораторна робота №7
ОБРОБКА ДВОВИМІРНИХ МАСИІВ
Мета роботи :ознайомлення із методами (алгоритмами) обробки двовимірних масивів (матриць) і створення відповідних комп’ютерних програм.